Codeforces Round 254 (Div. 2)
A.DZY Loves Chessboard (签到)
题意
给你一个N×M的地图 再空地上填上白棋或者黑棋要求同色棋子不能相邻
思路
直接搜索一下
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=5e4+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
char s[150][150];
int n,m;
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};
void dfs(int x,int y,bool f){
if(f)s[x][y]='W';
else s[x][y]='B';
for(int i=0;i<4;i++){
int xx=x+dx[i];
int yy=y+dy[i];
if(xx<0||xx>=n||yy<0||yy>=m||s[xx][yy]!='.'){
continue;
}
dfs(xx,yy,f?false:true);
}
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>s[i];
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(s[i][j]=='.'){
dfs(i,j,0);
}
}
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cout<<s[i][j];
}
cout<<endl;
}
return 0;
}
B - DZY Loves Chemistry (联通块)
题意
有一堆化学品,他们有的两个之间有化学反应,现在按一定顺序投放到一个试管中,如果投放之前试管内部有可以与当前投放的反应那么答案×2 怎么样投放答案最大,输出最大答案
思路
很容易想到最优答案就是可以反应的联通块的大小-1次方,然后多一个联通快就少1,那么答案就是总数减去联通快个数次方
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=5e4+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int fa[maxn];
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
ll n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int a,b;
cin>>a>>b;
a=find(a),b=find(b);
fa[a]=b;
}
ll ans=0;
for(int i=1;i<=n;i++){
if(fa[i]==i)ans++;
}
cout<<(1LL<<(1LL*n-ans*1LL));
return 0;
}
C - DZY Loves Physics (结论)
题意
给你一个图,定义图的密度是图的点值/两点之间的边值
让你找出一个联通封闭诱导子图 使得图的密度最大
思路
假设两个点的答案是最大的 那么答案为
\[\frac{u+v}{c}
\]
u和v是两个结点的值 c是他们之间的边的值
对于大于两个点的答案为
\[\frac{\sum u+\sum v}{\sum c}
\]
假设B的值为这个答案
\[B=\frac{\sum u+\sum v}{\sum c}
\]
那么对于任意一条边的值
对于任意的
\[\frac{u+v}{c} <B \\then\\u+v<Bc
\]
可以变成
\[\sum u+\sum v <B\sum c
\]
那么这样会得出
\[B>\frac{\sum u+\sum v}{\sum c}
\]
与上面矛盾 证毕
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=5e4+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
double a[maxn];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
int n,m;
double ans=0;
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
while(m--){
int u,v,w;
cin>>u>>v>>w;
ans=max(ans,double((a[v]+a[u])/w));
}
cout<<fixed<<setprecision(15);
cout<<ans;
return 0;
}
D - DZY Loves FFT (随机数乱搞理论)
题意
给出一个随机数组A,B,让你对于每个
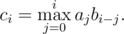
求出Ci
思路
可以发现A,B是完全随机的,而且暴力复杂度爆炸,
从大到小枚举排列中的数,再不断更新答案.更新过的答案就不需要再更新了
开一个优先队列保存起来,然后就是判断这前多少大的数据可不可以被取到,对于一个数钱50大的数对于他来说都没办法被取到的概率大概是
A50取50的概率分之一
优先队列的size越大概率越小
如果是在取不到就暴力一下把
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll x,n,d;
ll a[maxn],b[maxn];
ll getNextX(){
x=(x*37+10007)%1000000007;
return x;
}
void initAB(){
int i;
for(i = 0; i < n; i = i + 1){
a[i] = i + 1;
}
for(i = 0; i < n; i = i + 1){
swap(a[i], a[getNextX() % (i + 1)]);
}
for(i = 0; i < n; i = i + 1){
if (i < d)
b[i] = 1;
else
b[i] = 0;
}
for(i = 0; i < n; i = i + 1){
swap(b[i], b[getNextX() % (i + 1)]);
}
}
priority_queue<pair<ll,int> >all;
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
cin>>n>>d>>x;
initAB();
vector<int>B;
for(int i=0;i<n;i++)if(b[i])B.push_back(i);
for(int i=0;i<n;i++){
all.push({a[i],i});
bool yes=false;
priority_queue<pair<ll,int> >now;
for(int j=0;j<50&&!all.empty();j++){
ll value=all.top().first;
int id=all.top().second;
if(!yes&&b[i-id]){
cout<<value<<endl;
yes=true;
}
now.push(all.top());
all.pop();
}
if(!yes){
ll ans=0;
for(int j=0;j<B.size()&&B[j]<=i;j++)ans=max(ans,a[i-B[j]]);
cout<<ans<<endl;
}
all=now;
}
return 0;
}
DZY Loves Colors (区间合点线段树)
题意
给出N个点M个操作
每个操作可以把一段区间染色 并且如果一个结点被染色那么他的value会增加abs(new-old)
另一个操作是求区间的value
思路
区间问题首先线段树和分块
都能做 我先说线段树,分块晚上在做
线段树,我们可以每次把一个染色的区间看成一个点,对于一次染色最多把三个区间看成一个结点,也就是logn的复杂度
所以答案就是mlogn
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int n,m;
void read(int &res){
res=0;
char c;
while(c=getchar(),c<48);
do res=(res<<3)+(res<<1)+(c^48);
while(c=getchar(),c>47);
}
inline void out(ll x)
{
if (x > 9) out(x / 10);
putchar(x % 10 + '0');
}
struct SegTree{
struct node{
int l,r,len,color,mid;
ll sum,lazy;
}my[maxn<<2];
void build(int o,int l,int r){
my[o].l=l,my[o].r=r,my[o].len=(r-l+1),my[o].mid=(l+r)/2;
my[o].sum=my[o].lazy=0;my[o].color=-1;
if(l==r){
my[o].color=l;
return;
}
int mid=(l+r)/2;
build(o<<1,l,mid);
build(o<<1|1,mid+1,r);
}
inline void up(int o){
my[o].sum=my[o<<1].sum+my[o<<1|1].sum;
if(my[o<<1].color==my[o<<1|1].color)my[o].color=my[o<<1].color;
else my[o].color=-1;
}
void mix(int o,ll val,int col){
my[o].lazy+=val;
my[o].sum+=1LL*my[o].len*val;
my[o].color=col;
}
void down(int o){
if(!my[o].lazy)return;
mix(o<<1,my[o].lazy,my[o].color);
mix(o<<1|1,my[o].lazy,my[o].color);
my[o].lazy=0;
}
void update(int o,int l,int r,int val){
if(my[o].l>=l&&my[o].r<=r&&~my[o].color){
mix(o,abs(val-my[o].color),val);
return;
}
int mid=my[o].mid;
down(o);
if(l<=mid)update(o<<1,l,r,val);
if(r>mid)update(o<<1|1,l,r,val);
up(o);
}
ll query(int o,int l,int r){
if(my[o].l>=l&&my[o].r<=r){
return my[o].sum;
}
down(o);
int mid=my[o].mid;
ll ans=0;
if(l<=mid)ans+=query(o<<1,l,r);
if(r>mid)ans+=query(o<<1|1,l,r);
return ans;
}
}seg;
int main()
{
read(n);read(m);
seg.build(1,1,n);
while(m--){
int type,l,r,val;
read(type);
if(type==1){
read(l);read(r);read(val);
seg.update(1,l,r,val);
}
else{
read(l);read(r);
out(seg.query(1,l,r));
puts("");
}
}
return 0;
}



