Luogu P1902 刺杀大使
Luogu P1902 刺杀大使
是最近做到比较有心得的一道题。
我做了两种方法:
- 最小生成树
- 二分+DFS
最小生成树
虽然从题目标签上来看,二分+DFS才是这道题的正解。但事实上我是先写出最小生成树的做法,可能是因为这种做法的思路比较自然,而且复杂度没那么玄学吧。
建图
将第 $1$ 行看作一个点(记为起点),将第 $n$ 行看作一个点(记为终点),此两点点权为 $0$ 。第 $2$ 行到第 $n-1$ 行每行 $m$ 个点,点权按题目中对应位置赋值。
将起点与第 $2$ 行的每个点连一条边;类似的,将第 $n-1$ 行的每个点与终点连一条边。第 $2$ 行到第 $n-1$ 行则是按四连通的方式连边。
在以上连边过程中,显然所连的都是无向边;由题意,每条边的边权定义为该边两个端点的点权中较大的那一个。
附上一幅样例对应的图:
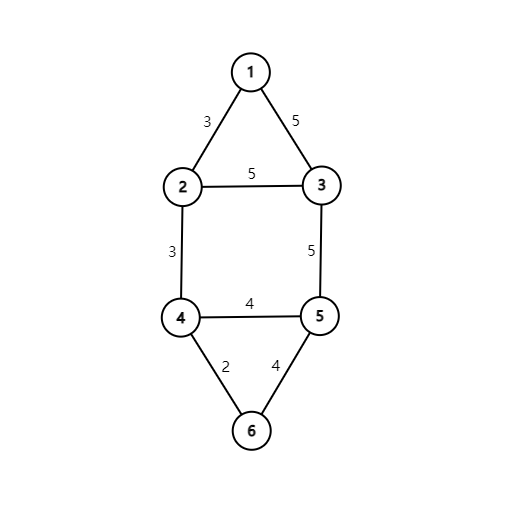
算法
这里用类似最小生成树的算法(我用的是Kruskal,Prim应当也是可以的)。
注意到按最小生成树算法中,按边权从小到大的方式遍历加边,这一思路能够得到本题所求的路线。只需将退出条件改为当起点与终点连通时退出,并调整更新答案的方式。
计算复杂度,不难得到边数为 $n^2$ 的级别。再根据Kruskal的复杂度,可知总复杂度为 $O(n^2 \log n^2)$。考虑到这里的 $n \leq 10^3$,是能够通过的。
代码
代码实现上,注意给点编号的方式。
#include<bits/stdc++.h>
#define N 1010
int n,m,siz,ans;
int p[N][N],fa[N*N];
struct node {
int u,v,w;
};
node edge[N*N*4];
namespace WalkerV {
void Read() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
scanf("%d",&p[i][j]);
}
}
return;
}
bool Compare(node x,node y) {
return x.w<y.w;
}
int Find(int x) {
return fa[x]==x?x:fa[x]=Find(fa[x]);
}
void Merge(int x,int y) {
fa[(Find(y))]=Find(x);
return;
}
void Kruskal() {
int cnt=0;
std::sort(edge+1,edge+siz+1,Compare);
for(int i=1;i<=siz;i++) {
if(Find(edge[i].u)!=Find(edge[i].v)) {
ans=std::max(ans,edge[i].w);
Merge(edge[i].u,edge[i].v);
i==1?cnt+=2:cnt++;
//printf("edge:%d %d %d\n",edge[i].u,edge[i].v,edge[i].w);
}
if(Find(1)==Find((n-2)*m+2)) {
return;
}
}
//printf("Fail\n");
return;
}
void Solve() {
for(int i=1;i<=m;i++) { //col1
edge[++siz]=(node){1,i+1,p[2][i]};
}
for(int i=2;i<=n-1;i++) { //col2~n-1
for(int j=1;j<=m;j++) {
if(j!=m) { //right
edge[++siz]=(node){(i-2)*m+j+1,(i-2)*m+j+2,std::max(p[i][j],p[i][j+1])};
}
if(i!=n-1) { //down
edge[++siz]=(node){(i-2)*m+j+1,(i-1)*m+j+1,std::max(p[i][j],p[i+1][j])};
}
}
}
for(int i=1;i<=m;i++) { //coln
edge[++siz]=(node){(n-3)*m+i+1,(n-2)*m+2,p[n-1][i]};
}
/*
for(int i=1;i<=siz;i++) {
printf("%d %d %d\n",edge[i].u,edge[i].v,edge[i].w);
}
*/
for(int i=1;i<=(n-2)*m+2;i++) {
fa[i]=i;
}
Kruskal();
return;
}
void Print() {
printf("%d\n",ans);
return;
}
}
int main()
{
WalkerV::Read();
WalkerV::Solve();
WalkerV::Print();
return 0;
}
二分+DFS
思路
注意到题目中“最大值最小”的表述,这把思路引向了二分。
我们二分题目所求的最小伤害代价。搜索则是常规的四连通寻路,并在前方点点权大于当前二分的答案时折返。
代码
代码实现上,注意每次二分时清空 $\texttt{vis}$ 数组。
搜索(尤其是还带有这种比较神奇的剪枝)的复杂度是难以计算(玄学)的。注意到还有以下几个减小常数的方法(我都没有用):
- 把二分的上限从理论上的 $p_{max}$(即 $1000$)调整为当前数据下的 $p_{max}$,这能减少几次DFS。
- 每次DFS前不清空 $\texttt{vis}$ 数组,而是改为记录到达每个点的次数来进行判断。
#include<bits/stdc++.h>
#define N 1010
#define INF 0x7FFFFFFF
#define debug printf("OK\n");
int n,m,ans,mid;
int p[N][N],d[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
bool vis[N][N];
namespace WalkerV {
void Read() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
scanf("%d",&p[i][j]);
}
}
return;
}
int DFS(int x,int y) {
if(x==n) {
return true;
}
vis[x][y]=true;
for(int i=0;i<=3;i++) {
int nx=x+d[i][0],ny=y+d[i][1];
//printf("(%d,%d)->(%d,%d)\n",x,y,nx,ny);
if(nx<1||nx>n||ny<1||ny>m||vis[nx][ny]||p[nx][ny]>mid) {
continue;
}
if(DFS(nx,ny)) {
return true;
}
}
return false;
}
int LowerBound(int l,int r) {
int ret=0;
while(r-l>=2) {
mid=(l+r)>>1;
memset(vis,false,sizeof(vis));
if(DFS(1,1)) {
ret=mid;
r=mid;
}
else {
l=mid;
}
//printf("l:%d r:%d mid:%d\n",l,r,mid);
}
return ret;
}
void Solve() {
ans=LowerBound(0,1001);
return;
}
void Print() {
printf("%d\n",ans);
return;
}
}
int main()
{
WalkerV::Read();
WalkerV::Solve();
WalkerV::Print();
return 0;
}
两种算法的比较

可见在这道题上搜索更快,而且空间也更小(毕竟是标签正解)。


