1 #include<iostream>
2 #include<stack>
3 #include<queue>
4 using namespace std;
5 typedef struct tnode TN;
6 typedef struct tnode* TT;
7 struct tnode{
8 int data;
9 TT left,right;
10 };
11 void creatree(TT &k) //前序遍历建立二叉树
12 {
13 int data1;
14 printf("请输入该分支的头节点：");
15 cin >> data1;
16 if (data1 ==-1)
17 k = NULL;
18 else{
19 k = (TT)malloc(sizeof(TN));
20 k->data = data1;
21 creatree(k->left);
22 creatree(k->right);
23 }
24 }
25 void preorder(TT root) //前序遍历
26 {
27 if (root){
28 printf("%d ", root->data);
29 preorder(root->left);
30 preorder(root->right);
31 }
32 }
33 ////////////四种非递归遍历方法
34
35 void preorder2(TT root) //前序遍历
36 {
37 stack<TT> sk;
38 TT wk = root;
39 while (wk || !sk.empty())
40 {
41 while (wk) //直到左子树为空的时候
42 {
43 sk.push(wk);
44 cout << wk->data << " ";
45 wk = wk->left;
46 }
47 if (!sk.empty())
48 wk= sk.top()->right; sk.pop(); //为空时栈顶为最短父节点，遍历该父节点的右子树
49 }
50 }
51 void midorder(TT root) //中序遍历
52 {
53 TT wk = root;
54 stack<TT> sk;
55 while (wk||!sk.empty())
56 {
57 while (wk)
58 {
59 sk.push(wk);
60 wk = wk->left;
61 }
62 if (!sk.empty())
63 {
64 wk = sk.top(); sk.pop();
65 cout << wk->data<<" ";
66 wk = wk->right;
67 }
68 }
69 }
70 void postorder(TT root) //后序遍历
71 {
72 stack<TT> sk;
73 TT wk = root; //工作指针
74 TT r = NULL; //标志指针
75 while (wk || !sk.empty())
76 {
77 if (wk){ //wk非空
78 sk.push(wk);
79 wk = wk->left;
80 }
81 else
82 {
83 wk = sk.top();
84 if (wk->right&&wk->right != r) //右子树存在且没有被访问过
85 {
86 wk = wk->right;
87 }
88 else
89 {
90 cout << wk->data << " ";
91 sk.pop();
92 r = wk; //表示该节点已经访问
93 wk = NULL; //下一步要么结束要么wk等于栈顶元素继续访问左子树或者右子树---所以令其为空
94 }
95 }
96 }
97 }
98 ////
99 void levelorder(TT root) //层次遍历
100 {
101 queue<TT> sk; //由层次遍历的特点：左子树先访问，而且左子树的孩子也先访问
102 TT wk = root;
103 sk.push(wk);
104 while (!sk.empty())
105 {
106 wk = sk.front();
107 cout <<wk->data << " ";
108 if (wk->left != NULL)sk.push(wk->left);
109 if (wk->right != NULL)sk.push(wk->right);
110 sk.pop();
111 }
112 }
113 int main()
114 {
115 TT st=NULL;
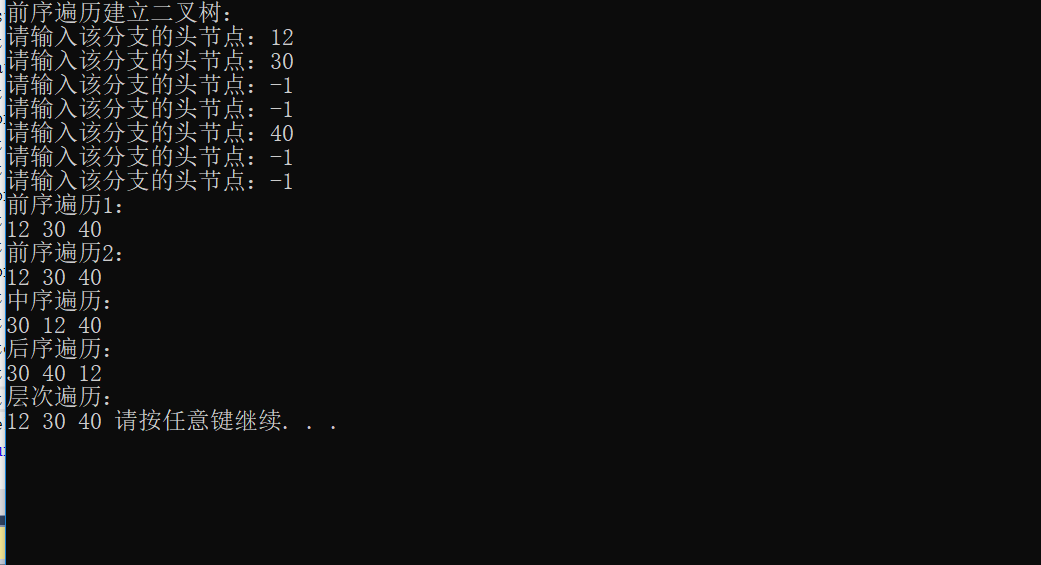
116 cout << "前序遍历建立二叉树："<<endl;
117 creatree(st);
118 cout << "前序遍历1：" << endl;
119 preorder(st);
120 cout << endl;
121 cout << "前序遍历2：" << endl;
122 preorder2(st);
123 cout << endl;
124 cout << "中序遍历：" << endl;
125 midorder(st);
126 cout << endl;
127 cout << "后序遍历：" << endl;
128 postorder(st);
129 cout << endl;
130 cout << "层次遍历：" << endl;
131 levelorder(st);
132 return 0;
133 }
