数据结构——树

0.PTA得分截图
1.本周学习总结（5分）
引入——树的递归和分治思想。
2.PTA实验作业（4分）
- 2.1 输出二叉树的每层结点
  - 2.1.1 解题思路及伪代码
  - 2.1.2 总结解题所用的知识点
- 2.2 目录树
3.阅读代码（0--1分）

| 这个作业属于哪个班级 | C语言--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业03--树 |
| 这个作业的目标 | 学习树的结构设计及运算操作 |
| 姓名 | 骆锟宏 |

0.PTA得分截图

在这里插入图片描述

1.本周学习总结（5分）

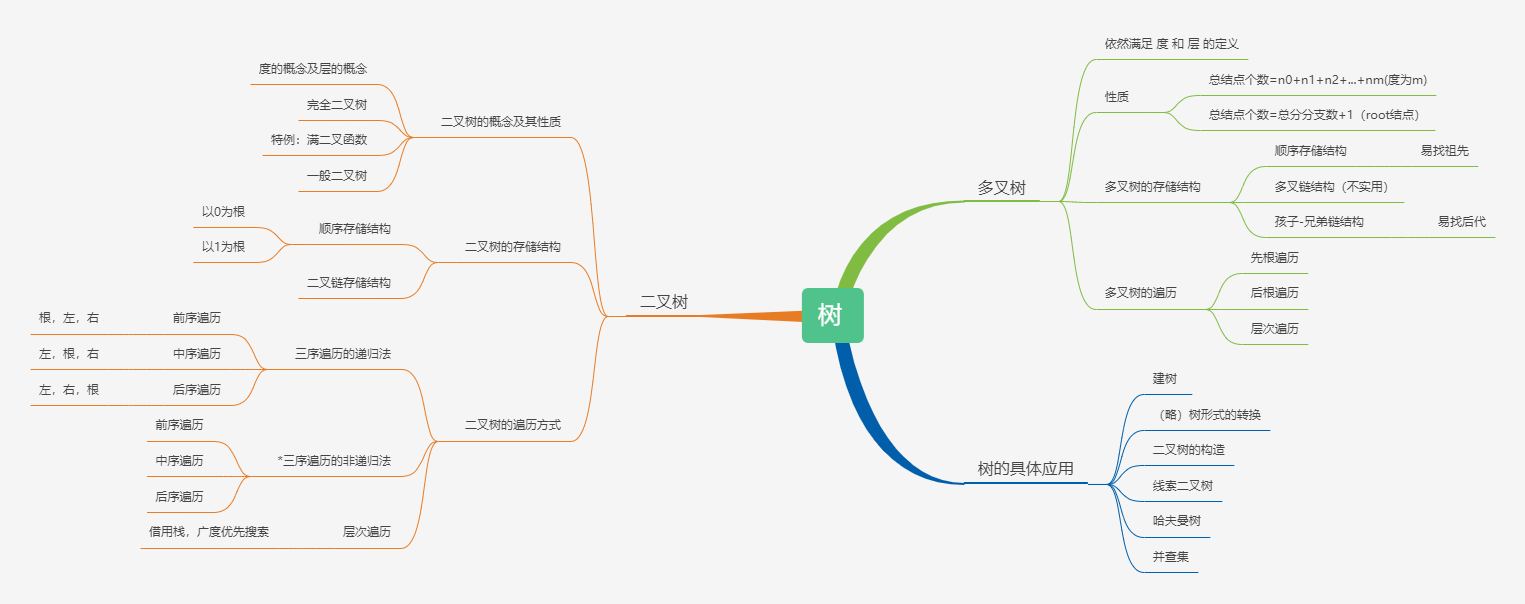
树的基本大框架：
树的具体应用的框架：

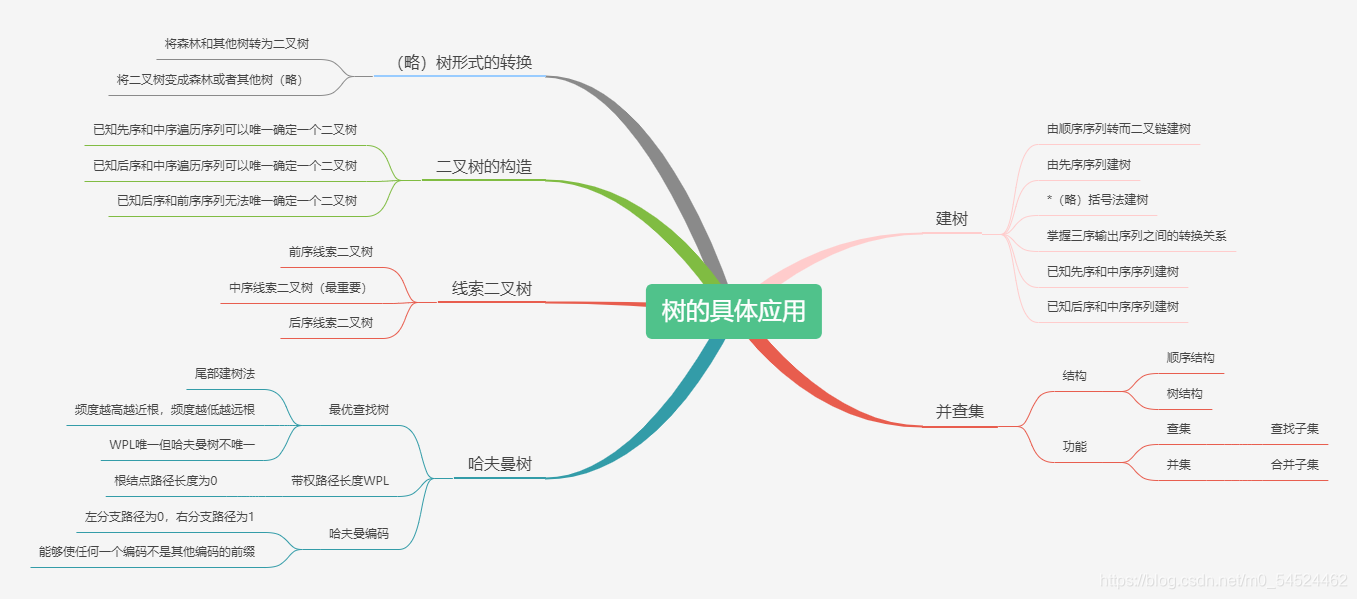
作者的话：如果你想对贯穿整个树应用的核心思想有一个大概的认识的话不妨从这个引入的小例子开始读起趴：

引入——树的递归和分治思想。

很明显的一个问题就是，树这种结构区别于以往我们所熟悉的线性结构，所以我们在考虑问题的时候就不能单纯
地使用一种一维的线性思维去考虑树的问题的解决了，而更多的时候，我们是用一种分治的思想，一种递归的思想，
这种思想在二叉树的例子，或者说他的具体代码实现中显得尤为显眼。二叉树就是很典型的分治处理的典范。
递归思想的数学映射，递归的本质是不断进行同一类操作，有微积分的感觉，但这种微分是有限的，逼近到问题的最简单的问题就是拆分的极限，这是把一个复杂的问题通过逻辑抽象，抽象成对同一类问题的不断求解，再把最后每个的结果不断积累起来，直到最上层，于是得到
了最后的答案。即先把一件大事不断分化成可以直接处理的最小情况，然后再把每层处理的结果累积起来得到最后的结果。而区别于积分不同的点在于，递归底层的结果会对上层有影响，不是简单的叠加关系，而是相关关系，这点要注意。
所以这里再次强调一下用递归思想解答题目的步骤：
- [找出递归关系]首先我们要找到上层量与次层量之间的逻辑关系。
- [找到递归出口]以为递归的拆分是有限的，所以要有一个代表拆分到最小度的标志。
- 最后才是根据递归关系和递归出口编写代码。
- 很重要的要提的一点是递归函数之间的联系靠的是函数的返回值，这点要好好利用。
  一道可以体现这个思想的PTA题目：

(递归与分治思想的例题)-----6-3 求二叉树高度 (20 分)

题目截图：
解题思路详细解释一下分支思想：
- 首先是这道题的递归关系：二叉树的高度等于其左右子树当中最高的子树的高度加一。
- 按这个关系去分治的话，最终会分治到空结点，那么对这个空节点来说，没有树，求这个树的高度自然高度就为0。
  而这就是这个分支关系的递归出口：当Tree == NULL,return 0。
- 接着就是去将递归关系解析为伪代码：
```
求左子树的高度lh
求右子树的高度rh
if(lh > rh)
return lh+1
else
return rh+1 
```
- 而求树的深度从上往下数和从下往上数效果相同，所以可以靠返回值
  从数的头顶不断往下累计直到返回数的高度。
以下是代码的具体实现：

int GetHeight(BinTree BT)
{
    int rHeight, lHeight;
    /*空树直接高度为零*/
    if (BT == NULL)
    {
        return 0;
    }

    /*一个很妙的递归算法*/
    lHeight = GetHeight(BT->Left);
    rHeight = GetHeight(BT->Right);

    if (lHeight > rHeight)
    {
        return (lHeight + 1);
    }
    else
    {
        return (rHeight + 1);
    }
}

1.0 树的基本概念和性质

1.0.1 树中的基本术语：

结点与度：树中某个结点的子树的个数称为该结点的度，而整个树中结点的度的最大值称为整颗树的度。
分支结点和叶子结点：树中度不为零的结点称为分支结点，树中度为零的结点称为叶子结点。
路径及路径长度：用比较简单的话来说，路径就是从一点出发，依次经过结点，最终到达目的结点的由结点和分支连成的线。而路径长度就是这条线包含的分支的数目，也等于包含的总结点个数减一。
孩子结点、双亲结点和兄弟结点：某一结点的后继结点被称为该结点的孩子结点，反之，该结点就被称为它孩子结点的双亲结点，而此时如果有另一个结点也是该结点的孩子结点的话我们就称这个结点为该结点的那个孩子结点的兄弟结点。
结点层次和树的高度：结点层次是从根结点开始定义的，树的根节点是第一层，往下依次递增层数。而树中结点的层数的最大值称为树的高度。
森林：多个互相独立的树构成一片森林，把一颗含有有个子树的树的根节点解放，就能得到一片森林。
二叉树、满二叉树、完全二叉树：二叉树是指度为2的树，具有很大的实用性，是重点研究的对象。满二叉树指所有的分支结点都为二分支结点，且叶子结点全部集中在层数最大的那一层的树，而完全二叉树实际上是满二叉树删除最右边的若干个叶子结点得到的树。

1.0.1 树中的基本性质：

树及二叉树的常见性质的图示：
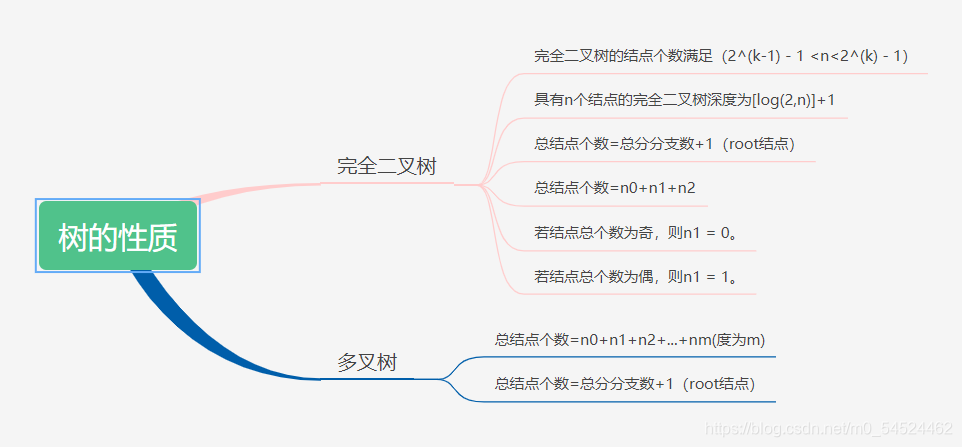
树的普遍性质：

树中的结点数等于所有结点的度数（也是总分支数）之和加一。
度为m的树中第i层上最多有m^(i-1)个结点（i >= 1）。
高度为h的m次树最多有 == (m^(h-1))/(m-1)个结点 == 。
具有n个结点的m次树的最小高度为[logm(n(m-1) +1)] (取大于等于中括号内值得最小整数)

二叉树的性质和特点的补充：

若完全二叉树存在度为1的结点的话，则该结点必为左叶子结点。

1.1 二叉树结构

1.1.1 二叉树的两种存储结构

顺序存储结构：

二叉树的顺序存储结构本质上采用的是数组（一组地址连续的存储单元）的数据结构，而用这种结构来存储的话，首先是要先对二叉树的每个结点进行编号处理通过编号来与数组的下标对应从而实现顺序存储。
那么问题来了编号有什么具体要求呢？
- 第一，就是要从根节点开始编号，有两种编号的形式：
  
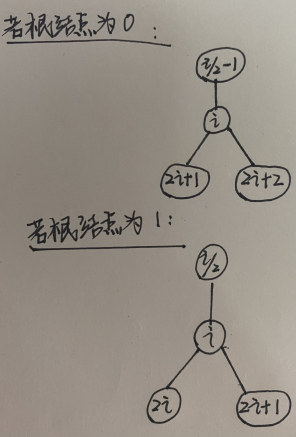
  区别在于根节点编号取1还是取0
- 第二，对于一般二叉树要先将其转化为完全二叉树，不存在的结点用虚结点来表示，用 “#”来作为他们的数据信息。
顺序存储结构的结构声明：

typedef ElemType SqBinTree[MaxSize];
//其中ElemType可以是任何基础数据结构或者自定义结构体。

顺序存储结构的优点：
- 可以利用数组元素的下标直接访问指定位置的结点数据。
- 当数是满二叉树或者完全二叉树时能够很大程度的节省存储空间。
- 最突出的优势在于方便查找。
顺序存储结构的缺点：
- 对于一般二叉树，当树的空结点很多的时候，使用顺序存储结构会造成空间的大量浪费。
- 顺序存储结构固有缺陷：执行插入和删除的操作十分不方便。

正是因为顺序存储结构有这些方面的缺陷，所以，对于树的一般结构，我们引出了链式存储结构来对它进行处理。

链式存储结构：

树中的每一个结点都用链表中的一个结点来表示，并且每一个结点都包含两个指针域（lchild/rchild）和一个数据域（data）。
链式存储结构的基本代码声明：

typedef struct BiTNode
{
	ElmentType data;//数据域
	struct BiTNode* lchild;//左孩子
	struct BiTNode* rchild;//右孩子
}BiTNode, * BiTree;

链式存储结构的优点：
- 链式存储结构在处理树的一般结构的时候，尤其是当数据量大，空结点多的情况下，能够很大程度地节省存储空间。
- 链式存储结构很方便进行树结点地插入和删除的操作。
- 链式存储结构方便查找某个结点的孩子，也方便查找后代。
链式存储结构的缺点：
- 要查找一个结点的双亲的话，需要扫描所有的结点，这一点相对比较费时间。
  - 但可以用增加一个指针域（parent）的方法来解决。

了解了树的具体的储存结构后，下一步就是要考虑如何根据已有的条件选择合适的存储结构，并创建出一个二叉树。

1.1.2 二叉树的构造

顺序存储结构的建树：

对顺序存储结构来建树的话，一般就是它给的输入直接是按结点编号的顺序的序列的话，就只需要知道它到底是从0开始编号还是从1开始编号，然后一个循环按顺序存入数组当中就可以了。
一般用不到这种建树方法，只是逻辑上可以存在而已。

将二叉树的顺序存储结构转化成二叉链来建树：

思维要点：
- 先确定根结点的起始编号，由此得到当前节点和它的后继结点的关系。
- 采用递归分别构造左子树和右子树。
- 当输入序列遍历到结尾的时候就代表树已经构造好了。
- 当遇到的元素是"#"时，让指针指向NULL。
代码层面的实现：

void CreateBiTree(string str, BiTree& T, int index)
{
	if (index > str.size()-1)
	{
        T = NULL;
		return;
	}
	if (str[index] == '#')
	{
		T = NULL;
	}
	else
	{
		T = new BiTNode;
		T->data = str[index];
		CreateBiTree(str, T->lchild, 2 * index);
		CreateBiTree(str, T->rchild, 2 * index + 1);
	}
}

如果根节点对应的下标是0，则需要改变：

		CreateBiTree(str, T->lchild, 2 * index );   --->   CreateBiTree(str, T->lchild, 2 * index + 1);  
		CreateBiTree(str, T->rchild, 2 * index + 1);   --->   CreateBiTree(str, T->rchild, 2 * index + 2);

这是很常见的一种建树方法，在已知给定序列是顺序序列和根结点编号的情况下，使用这种建树方法很方便。

给定树的前序遍历序列建树：

思维要点：
- 首先要了解前序序列的特点，前序序列从左往右的元素性质是先根节点在左子树结点，然后等所有的左子树结点都输出的时候，才开始输出最后一个子树的右节点然后往下都是右子树的结点数据。
- 所以很明显需要用到递归按先建根树后建左子树，最后建右子树的顺序来。
- 其中需要有一个不断在增加的变量来记录当下扫描到了序列的哪一个位置了，记作当前下标。
- 以及重要的点是每建完一个树后，当前下标要自增1，代表这个结点已经建好了。
- 当序列扫描结束的时候 （当前下标大于序列长度减一时）(如果采用的是字符数组的结构的话，可以用字符数组自带的 ’\0‘ 结束符来判断当下是否到了尾部) ，表示建树完成，直接返回。
- 当遇到元素是“#”的时候，将指针指向空，让当前下标下移（加一）。
- 正常建树的话，也要记得创建好结点后，要让当前下标下移。
具体代码实现如下：

void CreateBiTree(char str[], BiTree& T, int& index)
{
	if (!str[index])//序列用字符数组来存
	{
		T = NULL;
		return;
	}
	if (str[index] == '#')
	{
		index++;
		T = NULL;
		return;
	}
	else
	{
		T = new BiTNode;
		T->data = str[index++];
		CreateBiTree(str, T->lchild, index);
		CreateBiTree(str, T->rchild, index);
	}
}
//或者可以写成这样子：
void CreateBiTree(string str, BiTree& T, int& index)
{
	if (index > str.size()-1)//序列用字符串来存
	{
		T = NULL;
		return;
	}
    
	if (str[index] == '#')
	{
		T = NULL;
		return;
	}
	else
	{
		T = new BiTNode;
		T->data = str[index];
		CreateBiTree(str, T->lchild, ++index);
		CreateBiTree(str, T->rchild, ++index);
	}
}

要特别注意的是这里的先序序列不是遍历二叉链结构得到的先序序列，而是先序遍历顺序存储结构得到的先序序列，这样的先序序列才能用来直接建树，如果是不给出空结点的位置的话，是无法单纯靠前序遍历输出得到的序列来建树的，那这种情况下要怎么做呢？这是后话，留个悬念。

没错当给定的序列是按二叉链结构遍历得到的前序、中序或后序序列的话，就需要提供两种序列才能惟一确定一棵树，并且只给出先序和后序序列无法直接确定一棵树

通过先序遍历序列和中序遍历序列构造二叉树：

思路
- 类似于前序遍历，不过是不断根据根节点的信息来建树，由前序遍历序列知道根节点的位置，然后再由中序遍历序列结合已知的根节点信息，把大树的序列不断分割为小树的序列。
- 那什么情况下是拆分到无法再拆分的情况呢？那就是以叶子结点的孩子结点为根节点的树，这个树的序列长度为0，是个空树，这也就是递归出口。
伪代码如下：

if -> 当前输入的序列长度为零->返回空树或者令当前树指向空。
查找当前树的根节点在中序序列中的位置
左子树的序列个数 = 根节点在中序序列的地址 - 中序序列首地址；
递归构造左子树；
递归构造右子树；

两种函数声明下的代码实现：

void CreateBTree(BTree& T, char* preorder, char* inorder, int n)
//BTree CreateBTree(char* preorder, char* inorder, int n)
{
    //BTree T;
    char* pMove;
    int distance;//代表中序序列中根结点距离序列头的距离；
    
    // 1. 结点个数为0就不需要再建树了
    if (n <= 0)
    {
        T = NULL;//这里别忘了要让树结点指向空！
        return;
        //return NULL;
    }
    
	//2. 创建新结点
    T = new BTNode;
    T->data = *preorder;

    //3. 在中序序列中查找根节点的位置
    for (pMove = inorder; pMove < inorder + n; pMove++)
    {
        if (*pMove == *preorder)
        {
            break;
        }
    }

    distance = pMove - inorder;

	//4.递归构造左、右子树
    CreateBTree(T->lchild ,preorder + 1, inorder, distance);//构造左子树
    CreateBTree(T->rchild ,preorder + distance + 1, pMove + 1, n - distance - 1);//构造右子树

    //T->lchild = CreateBTree(preorder + 1, inorder, distance);//构造左子树
    //T->rchild = CreateBTree(preorder + distance + 1, pMove + 1, n - distance - 1);//构造右子树
    //return T;
}

通过后序遍历序列和中序遍历序列构造二叉树：

思路
- 本质上和前面的通过前序遍历序列和中序遍历序列构造二叉树的大题思路一致，都是都过不断拆分子树，针对子树的根结点为对象来构造二叉树。
- 说说和前面的方法不一样的一些点吧
  - 首先是后序序列的根节点在序列的尾部所以T->data = postorder[n-1];
  - 以及在查找的过程中，与中序序列的元素逐个对比的也应该是这个元素。
  - 在递归构造函数的时候，传入的后序序列的表示方式要改变。
  - CreateBTree(T->lchild, postorder, inorder, distance);//构造左子树
  - CreateBTree(T->rchild, postorder + distance, pMove + 1, n - distance - 1);//构造右子树}
  - 不过拆分子树的标准依然是寻找根节点在中序序列中的位置，然后算出左子树的序列长度。
代码层面：

void CreateBTree(BTree& T, ElementType* postorder, ElementType* inorder, int n)
{
    ElementType* pMove;
    int distance;//代表中序序列中根结点距离序列头的距离；
    //结点个数为0就不需要再建树了
    if (n <= 0)
    {
        T = NULL;
        return;
    }


    T = new BTNode;
    T->data = postorder[n-1];

    //在中序序列中查找根节点的位置
    for (pMove = inorder; pMove < inorder + n; pMove++)
    {
        if (*pMove == postorder[n-1])
        {
            break;
        }
    }

    distance = pMove - inorder;

    CreateBTree(T->lchild, postorder, inorder, distance);//构造左子树
    CreateBTree(T->rchild, postorder + distance, pMove + 1, n - distance - 1);//构造右子树
}

小要点：
- 首先同样的依然也可以有两种函数的定义，此处给出的是void类型的。
- 另外一点就是，考虑到输入的序列信息可能是字符，也可能是数字，于是在这个地方我把遍历序列统一改为ElementType*,这样在具体问题中，就只需要在开头定义处，根据具体情况对typedef进行改动就可以啦。

课本上给出了一种比较麻烦的建树方法：括号法建二叉树，这里占个位置但暂时不讨论。

1.1.3 二叉树的遍历

前序遍历二叉树

前序遍历二叉树的核心思想主要是对于每一个树来说，都是优先访问根节点，然后访问左子树，最后访问右子树。
递归代码实现：

void PreorderPrintNodes(BinTree BT)
{
    if (BT == NULL)
    {
        return;
    }
    cout << BT->Data;
    PreorderPrintNodes(BT->Left);
    PreorderPrintNodes(BT->Right);
}

对于前序遍历有一个很简单的记忆方法，那就是先序遍历得到的结果等效于，从树根出发绕着树的外部轮廓走一圈，将依次经过的结点的信息输出，得到的排列就是前序遍历序列
不妨拿棵树来举个试一试：
以PTA[7-4 jmu-ds-输出二叉树每层节点 (22 分)]的图为例：
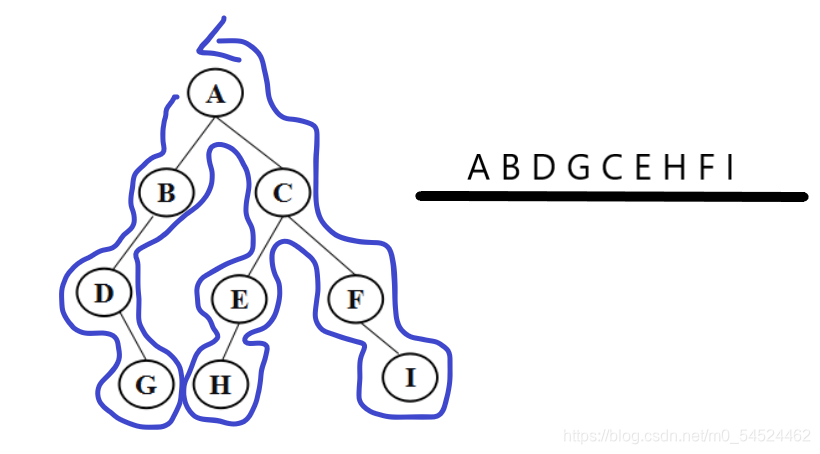
你会惊奇的发现，一旦你画出了树的图后，只需要从根节点绕着树的外部轮廓把依次经过的结点按先后顺序写下来，你就能得到该二叉树的先序遍历序列。

中序遍历二叉树

中序遍历二叉树的核心思想主要是对于每一个树来说，都是优先访问左子树，然后访问根节点，最后访问右子树。
递归代码实现：

void InorderPrintNodes(BinTree BT)
{
    if (BT == NULL)
    {
        return;
    }
    InorderPrintNodes(BT->Left);
    cout << BT->Data;
    InorderPrintNodes(BT->Right);
}

同样的，对于中序遍历也有一个很简单的记忆方法：画出树的图形后，只需要让二叉树的每个结点落到对应的横向上的投影，那此时横向上结点排序的顺序就是二叉树的中序遍历序列，更简单地来说就是不看树的高度，以人类直觉将树的结点从最左往最右写下来，那这个排序的序列就是二叉树的中序遍历序列。
不妨拿棵树来举个试一试：
还以PTA[7-4 jmu-ds-输出二叉树每层节点 (22 分)]的图为例：

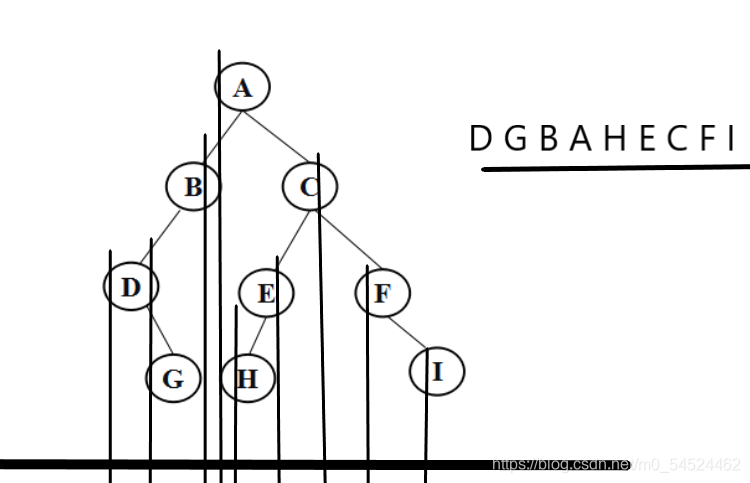
后序遍历二叉树

后序遍历二叉树的核心思想主要是对于每一个树来说，都是优先访问左子树，然后访问右子树，最后访问根节点。
递归代码实现：

void PostorderPrintNodes(BinTree BT)
{
    if (BT == NULL)
    {
        return;
    }
    PostorderPrintNodes(BT->Left);
    PostorderPrintNodes(BT->Right);
    cout << BT->Data;
}

同样的，对于后序遍历也有一个很简单的记忆方法：不妨把整颗树当成一束二维的葡萄，我们像先序遍历那时候一样，从根结点出发，绕着这个葡萄的外围轮廓走，当我们的轮廓曲线包住只有一颗葡萄（也就一个结点）的时候，把这个结点摘下来，排上去，不断这样做，直到最后，把根节点放在最后，得到的序列就是后序遍历序列。
不妨拿棵树来举个试一试：
依然以PTA[7-4 jmu-ds-输出二叉树每层节点 (22 分)]的图为例：
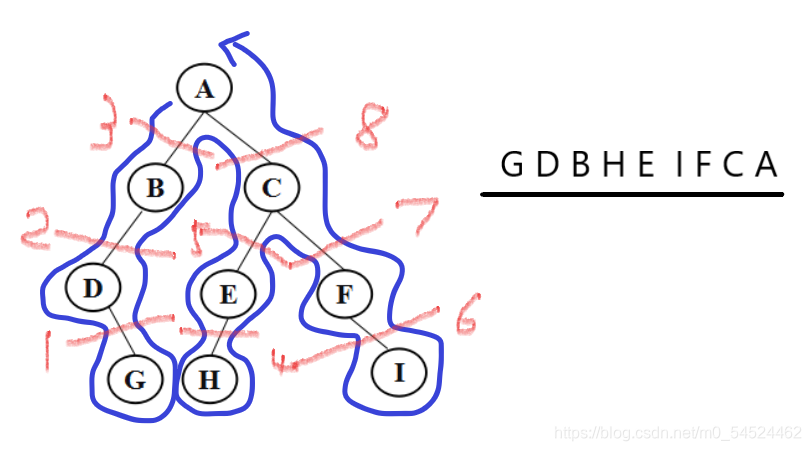
这里给出一个用来测试三种特殊方法是否合理的程序：
文中所用的例子树的输入是：ABD#G###CEH###F#I##

#include <iostream>
#include<string>
using namespace std;

typedef char ElementType;
typedef struct BTNode {
    ElementType Data;
    struct BTNode* Left;
    struct BTNode* Right;
}BTNode, * BiTree;


/*前序遍历法建二叉树*/
void CreateBiTree(string str, BiTree& T, int& index)
{
    if (index > str.size() - 1)
    {
        T = NULL;
        return;
    }
    if (str[index] == '#')
    {
        index++;
        T = NULL;
        return;
    }
    else
    {
        T = new BTNode;
        T->Data = str[index++];
        CreateBiTree(str, T->Left, index);
        CreateBiTree(str, T->Right, index);
    }
}

void PreorderPrintNodes(BiTree BT)
{
    if (BT == NULL)
    {
        return;
    }
    cout << BT->Data;
    PreorderPrintNodes(BT->Left);
    PreorderPrintNodes(BT->Right);
}

void InorderPrintNodes(BiTree BT)
{
    if (BT == NULL)
    {
        return;
    }
    InorderPrintNodes(BT->Left);
    cout << BT->Data;
    InorderPrintNodes(BT->Right);
}

void PostorderPrintNodes(BiTree BT)
{
    if (BT == NULL)
    {
        return;
    }
    PostorderPrintNodes(BT->Left);
    PostorderPrintNodes(BT->Right);
    cout << BT->Data;
}


int main()
{
    string str;
    cin >> str;
    BiTree tree;
    int start_val = 0;
    CreateBiTree(str, tree, start_val);

    cout << "前序遍历序列是：";
    PreorderPrintNodes(tree);
    cout << endl;

    cout << "中序遍历序列是：";
    InorderPrintNodes(tree);
    cout << endl;

    cout << "后序遍历序列是：";
    PostorderPrintNodes(tree);
    cout << endl;

    return 0;
}

得到的效果：

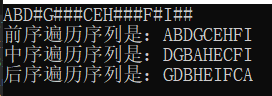
作者的话：
仔细观察的话，你会发现采用递归方式去实现三序遍历本质上的差别只不过体现在了输出语句的位置上，如果是前序就放在最前面，中序就放在对左右子树递归遍历的中间，后序就放在后面。
事实上，这三种遍历方式还有非递归的做法，但不变的是，非递归的做法本质上只是把递归没有显化的过程显化了而已，是借用了队列的结构来进行具体的实现。至于具体的实现过程可以拜读一下这篇博客：写得比较详细。也可以参考课本第218页开始的内容。

博文转载二叉树非递归实现三序遍历的博文

版权声明：该文为CSDN博主「小心眼儿猫」的原创文章，遵循CC 4.0 BY-SA版权协议，今转载并附上原文出处链接及声明。
原文链接：https://blog.csdn.net/qq_40927789/article/details/80211318
原文作者：https://blog.csdn.net/qq_40927789

层次遍历二叉树

思路：借用队列的结构，先让根节点入队，此时队列不空，然后再通过循环，每次让队首的结点出队后，就输出队首元素，若队首结点的孩子结点不为空，就让队首元素的孩子按先左后右的顺序，从队列的尾部插入，当队空的时候，循环结束，此时表明该树已经层次遍历结束。
代码实现：

/*层序遍历法输出二叉树*/
void levelOrder(BiTree Troot)
{
	//空树莫得打印
	if (Troot == NULL)
	{
		cout << "NULL";
		return;
	}
    
	int flag = 1;
	queue<BiTree> Tqueue;
	//if(Tqueue.empty())
        Tqueue.push(Troot);
	while (!Tqueue.empty())
	{
		BiTree tempPtr = Tqueue.front();
		Tqueue.pop();

		if (flag)
		{
			cout << tempPtr->data;
			flag = 0;
		}
		else
		{
			cout << " " << tempPtr->data;
		}

		if (tempPtr->lchild)
		{
			Tqueue.push(tempPtr->lchild);
		}
		if (tempPtr->rchild)
		{
			Tqueue.push(tempPtr->rchild);
		}
	}
}

层次遍历思维的应用----求二叉树的宽度：
- 具体代码实现：

/*类层次遍历法获取树的最大宽度*/
int GetMaxWidth(BiTree T)
{
	if (!T)
	{
		return 0;
	}
	queue<BiTree> Que;
	int max = 1;
	int len;//储存树每层元素的个数，同时也是每层队列的长度。
	Que.push(T);
	while (!Que.empty())
	{
		len = Que.size();
		while (len > 0)//代表当前层还有元素在队列中
		{
			BiTree tempT = Que.front();
			Que.pop();
			len--;
			if (tempT->lchild != NULL)
			{
				Que.push(tempT->lchild);
			}
			if (tempT->rchild != NULL)
			{
				Que.push(tempT->rchild);
			}
		}
		if (Que.size() > max)
		{
			max = Que.size();
		}
	}
	return max;
}

具体来看的话，核心思想还是二叉树的层次遍历，只不过它细化了层次遍历中循环内部不断入队与出队的过程，它借用变量len来记录树的每一层的结点个数（也就是每一层的宽度）,以此来实现对二叉树进行一层一层的入队和出队的控制，从而能得到树每一层的宽度，最后通过不断对比得到每层宽度的最大值为该树的宽度。
三序遍历的深化的理解方法来自于该篇博客：
想要更清晰地了解这4种遍历方式可以拜读一下这篇博客：二叉树的4种遍历方式

版权声明：该文为CSDN博主「流楚丶格念」的原创文章，遵循CC 4.0 BY-SA版权协议，今转载并附上原文出处链接及声明。
原文链接：https://blog.csdn.net/weixin_45525272/article/details/105837185
原文作者：https://yangyongli.blog.csdn.net/

从该文章对4种遍历方式的深入思考非常妙，用另一种很常识和有趣的方法让我们能够很简单地记住二叉树的三序遍历方法，这也提醒要让人能更直观地去了解某些知识点，可以尝试采用一种不那么专业性强的叙述方式去讲述，可能得到的效果会更好。

1.1.4 线索二叉树

背景，为什么会引申出线索二叉树？
- 假设一个二叉树有n个结点，每个结点有两个指针域，那就一共有2n个指针域，但实际被用到的指针域只有n-1个，还有n+1个指针域没有被使用，但是不可否认的是，这些指针域依然会占用内存，所以与其浪费这些指针域不如将他们利用起来，于是就有了线索二叉树的概念。
- 那问题来了，怎么用起来呢？由于二叉树结构在查找前驱和后继上存在一定的缺陷，所以决定将这些指针域用来填补这个空缺，于是我们就能够得到：
我们将原本在二叉树中指向NULL的指针利用起来，如果这个指针是左指针，那就用它来指向该结点的前驱结点，如果这个指针是右指针，那就让它来指向该结点的后继结点。
那么这时问题来了？ 我现在怎么判断我的指针究竟指向的是孩子结点还是前驱后继呢？所以就要引入一个标签变量，当标签变量的值为1的时候，就代表指针是线索，指向前驱或者后继结点，而当标签变量为0的时候，就代表指针是孩子指针。
这时问题又来了？ 怎么判断当前结点的前驱结点是什么，后继结点是什么呢？很明显这和具体给出的结点排序的序列有关，而我们知道，对于二叉树，我们有三种排序序列-----前序序列、中序序列以及后序序列，所以当然的，线索二叉树也分别对应有三种类型的线索二叉树。

简要介绍一下前序线索二叉树和后续线索二叉树的特点：

前序线索二叉树
- 若结点是二叉树的根节点则前驱为空。
- 结点的后继：若有左孩子，则左孩子就是其后继，若没有左孩子但有右孩子，则右孩子就是其后继，若是叶子结点右标签为1，则右链为线索，指向其后继；
- 结点的前驱：若没有左孩子其左标志为 1 ，则左链为线索，指向其前驱；否则，有左孩子，无法存储左链，不能直接找到其前驱结点。
后序线索二叉树
- 若结点是二叉树的根节点则后继为空。
- 结点的前驱：如果有右孩子，那右孩子就是其前驱，如果没有右孩子有左孩子，那左孩子就是其前驱；如果没有左孩子，那左指针也就是线索，指向前驱。
- 结点的后继：如果没有右孩子，那右指针是线索，指向后继；如果有右孩子，则无法存储右链，不能直接找到其后继结点。
在简化一点的记忆方式就是：如果有线索指针就可以直接知道，如果没有线索指针的话，1. 就先看当前结点的位置关系，它是哪棵树的根，又是谁的左孩子或者右孩子，又是谁的双亲，2. 然后对应不同对应序列的遍历顺序（根左后、左右根），来判断具体的前驱后继。
比如针对前序序列，在一个子树内，左孩子结点的前驱结点就肯定是该子树的根结点，而要找该根结点的前驱，就要看这个根节点到底是谁的孩子，一步一部往前找而已。

中序线索二叉树特点：

中序线索二叉树基于中序遍历的特点（左根右），如果我们都是以视当前结点为某一子树的根节点的话,那很轻松的可以知道：
在中序线索树中，若某结点有右孩子，则其后继结点是它的右子树的最左下结点；在中序线索树中，若某结点有左孩子，则其前驱结点是它的左子树的最右下结点。
这里要注意最右下的概念和最左下的概念。这两个要求都是要同时满足两个最端。
从图中来直观体验一下线索二叉树是怎么构建的吧：
需要补充的一点是对于中序线索二叉树一般我们会引入一个新结点来，按图上来看就是让B的左指针和F的右指针同时指向的一个结点，然后这个结点的两个指针域都同时指向根节点A。这样处理的话，就可以把中序线索二叉树连通化。
中序二叉树的代码方面的实现：
- 中序线索二叉树的线索化：（课本第235页）
- 中序线索二叉树的遍历：（课本第236页）

1.1.5 二叉树的应用--表达式树

表达式树的代码

表达式树的构造

大概思路：
- 表达式树是一种以运算符为根节点，以运算数为左右孩子的树，对于这种根节点与孩子有明显特点的树，就可以使用从尾部开始建树的非递归式的建树方法。
- 在这个问题中我们需要借助两个栈作为辅助的数据结构，一个是运算符栈，另一个是操作数栈。
伪代码：

while（遍历没到字符串尾）
{
	if 新节点存的数据的数字，就让这个新节点进入操作数栈，
	if 新节点存的数据是操作符
		if 运算符栈栈空，直接入栈。
		else if 将入栈运算符等级更高，直接入栈
		else 出栈一个栈内运算符为根节点，依次出栈两个操作数栈元素为右孩子左孩子建树，并将建好的树放入操作数栈。
}
if(运算符栈空)
{
return 操作数栈栈顶元素；
}
else
{
while（运算符栈不空）
{
不断出栈建树。
}
return 操作数栈栈顶元素；
}

具体代码：

void InitExpTree(BTree& T, string str)//建表达式的二叉树
{
    stack<BTree> numberStack;/*储存分支结点，或者说操作数的栈*/
    stack<BTree> signStack;/*储存根结点，或者说运算符的栈*/
    char cur_char;
    /*优先遍历输入的字符串*/
    for (int i = 0; i < str.size(); i++)
    {
        cur_char = str[i];
        if (In(cur_char))
        {
            while (1)
            {
                if (signStack.empty()
                    || Precede(signStack.top()->data, cur_char) == '<')/*入栈的条件判断*/
                {
                    BTree signTNode = new BiTNode;
                    signTNode->data = cur_char;
                    signStack.push(signTNode);
                    /*运算符入栈是该运算符流程结束的标志之一*/
                    break;
                }
                else if (Precede(signStack.top()->data, cur_char) == '>')/*出栈的条件判断*/
                {
                    char sign = signStack.top()->data;
                    signStack.pop();
                    BTree newNumb;
                    BTree rTree = numberStack.top();
                    numberStack.pop();
                    BTree lTree = numberStack.top();
                    numberStack.pop();
                    /*然后开始建一个小二叉树*/
                    CreateExpTree(newNumb, lTree, rTree, sign);
                    numberStack.push(newNumb);
                }
                else if (Precede(signStack.top()->data, cur_char) == '=')
                {
                    signStack.pop();
                    break;
                }
            }
        }
        else/*cur_char为数字*/
        {
            BTree numbTNode = new BiTNode;
            numbTNode->data = cur_char;
            numbTNode->lchild = NULL;
            numbTNode->rchild = NULL;
            numberStack.push(numbTNode);
        }
    }


    if (signStack.empty())
    {
        T = numberStack.top();
        return;
    }
    else
    {
        while (!signStack.empty())
        {
            char sign = signStack.top()->data;
            signStack.pop();
            BTree newNumb;
            BTree rTree = numberStack.top();
            numberStack.pop();
            BTree lTree = numberStack.top();
            numberStack.pop();
            /*然后开始建一个小二叉树*/
            CreateExpTree(newNumb, lTree, rTree, sign);
            numberStack.push(newNumb);
        }

        T = numberStack.top();
        return;
    }

}

计算表达式树

大概思路：
- 由于最简单的计算都需要两个操作数和一个运算符，而一个操作数又可以被视为一个简单计算的结果，所以，对表达式树的计算可以采用递归的思想。
- 根据根节点的具体符号来进行递归调用运算，每颗子树不断调用下来，最终会调用到空树，可以视该树的计算结果为0进行返回。
伪代码：

if(当前结点为NULL)  return 0；//递归出口
if(当前的结点是数字)；return 数字字符 - '0';
else//当前的结点是运算符：
	switch (运算符)
	case ‘+’：return 计算左子树的值 + 右子树的值
	case ‘-’：return 计算左子树的值 - 右子树的值
	case ‘*’：return 计算左子树的值 * 右子树的值
	case ‘/’：if(右子树的值不为0)
					{ return 计算左子树的值 /右子树的值 }
					else
					{ 输出error! }

具体代码：

double EvaluateExTree(BTree T)//计算表达式树
{
    if (T == NULL)
    {
        return 0;/*该数字并未被利用*/
    }

    if (In(T->data))
    {
        switch (T->data)
        {
        case '+':
            return EvaluateExTree(T->lchild) + EvaluateExTree(T->rchild);
        case '-':
            return EvaluateExTree(T->lchild) - EvaluateExTree(T->rchild);
        case '*':
            return EvaluateExTree(T->lchild) * EvaluateExTree(T->rchild);
        case '/':
            if (EvaluateExTree(T->rchild) == 0)
            {
                cout << "divide 0 error!" << endl;
                exit(0);/*直接退出程序*/
            }
            else
            {
                return EvaluateExTree(T->lchild) / EvaluateExTree(T->rchild);
            }
        default:
            break;
        }
    }
    else/*当结点值为数字的时候*/
    {
        return ((double)T->data - '0');
    }
}

1.2 多叉树结构

1.2.1 多叉树结构

树的顺序存储结构：

typedef struct 
{　 ElemType data;	//结点的值
　   int parent;		//指向双亲的位置(伪指针)
} PTree[MaxSize];

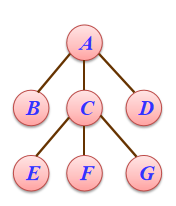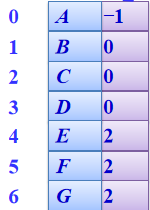
在这里插入图片描述 ----->>>

顺序存储结构方便找祖先，但是不方便找后代。

孩子链结构

typedef struct node
{      ElemType data;		  //结点的值
        struct node *sons[MaxSons];	      //指向孩子结点
}  TSonNode;

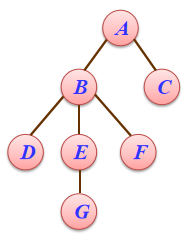
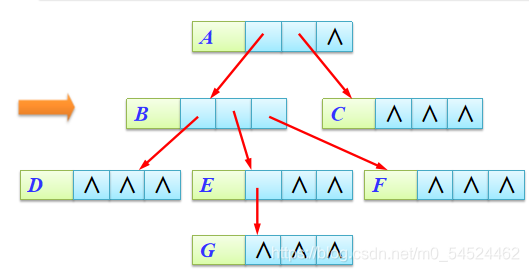
在这里插入图片描述

孩子链结构方便找孩子，但是不方便找双亲，而且会浪费很多指针域的空间！

孩子兄弟链结构

typedef struct tnode 
{      
       ElemType data;	//结点的值
       struct tnode *firstchild;  //指向孩子结点
       struct tnode *brother; //指向兄弟 
} TSBNode,* TSBTree;

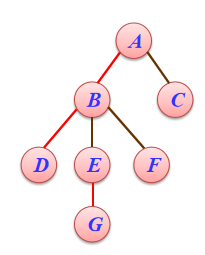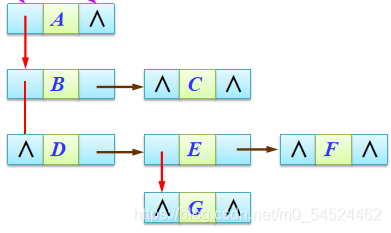
在这里插入图片描述 ---->>>

这个结构能很好的地解决孩子链中空指针过多而导致的空间浪费的问题。
但同样的，存在链式结构固有的找双亲麻烦的问题。
每个结点固定只有2个指针域，并且顺序不能颠倒！

1.2.2 多叉树遍历

先根遍历

若树不空，则先访问根结点，然后依次先根遍历各棵子树。
记忆方法，二叉树中的绕树的外部轮廓走的方法依然适用，以课件中的例子为例：
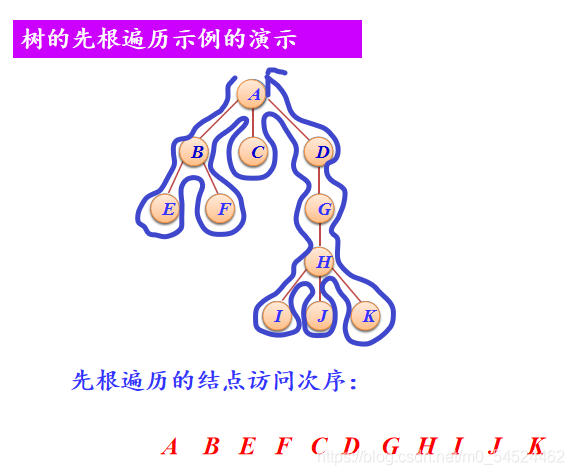
从树的根节点开始以逆时针方向绕着树的轮廓爬行，按遇到结点的先后顺序输出所遇到的结点，最后得到的输出序列就是树的先根遍历序列。

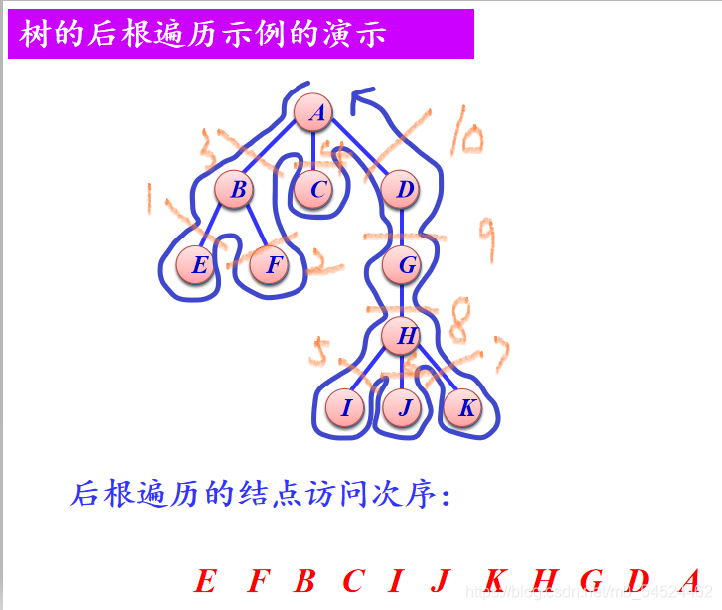
后根遍历

若树不空，则先依次遍历各棵子树，然后再访问根结点。
记忆方法，二叉树中的绕树的外部轮廓走然后绕住一颗葡萄（结点）就切下来一颗的方法依然适用，以课件中的例子为例：

层次遍历

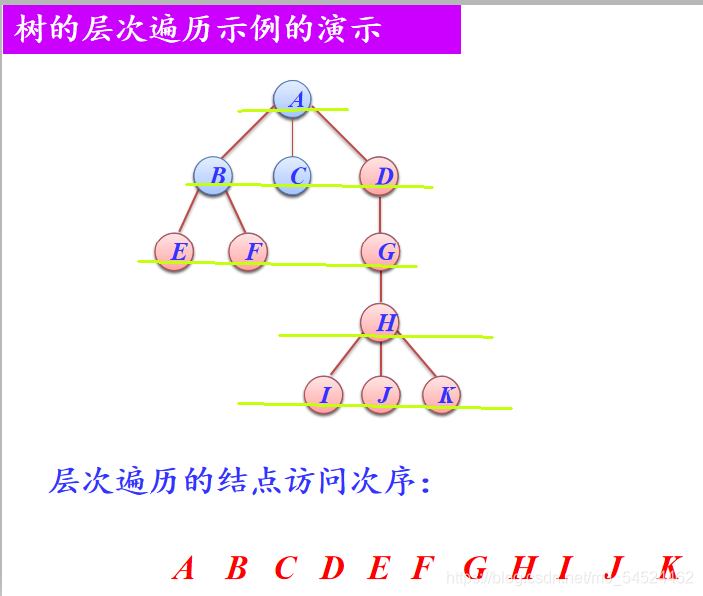
若树不空，则从上到下，从左到右一层一层访问树的每个结点。
记忆方法：其实层次遍历只要能画出树的图就可以看着直接写出来了。

1.3 哈夫曼树

1.3.1 哈夫曼树定义

要理解哈夫曼树首先要理解一个概念就是WPL（带权路径长度）：在许多的应用中经常将树的结点赋予一个有某种意义的数值，我们称其为权值，从根节点到该结点的路径长度乘以该结点的权值得到的数值我们称其为该结点的带权路径长度，而树中所有结点的带权路径长度之和我们称其为整棵树的带权路径长度。
有了WPL这个衡量的值之后，哈夫曼树的定义也就呼之欲出----n个带权叶子结点所构成的所有二叉树中，WPL最小的那个树称为哈夫曼树或者最优二叉树。
由此会产生出一个特性：哈夫曼树中，权值越大的结点会越靠近根节点，而权值越小的结点会越远离根节点。 也是这个特性赋予了哈夫曼树在查找方面有最优的特性。

那么问题来了，哈夫曼树能解决什么问题捏？

从我们有接触到的题目来看，首先哈夫曼树最直接的应用就是哈夫曼编码，通过构造哈夫曼树得到的哈夫曼编码能有效地避免某一个编码会是其他编码的前缀的问题，从而解决会在解码的时候引发错解的问题，同时，经过哈夫曼编码的编码能实现编码效率的最大化，有利于信息快速传输，因为它减少了信息的存储空间。
第二从定义出发，哈夫曼树的定义来源于树的WPL，并且是最小的WPL，所以利用哈夫曼树来查找的话，我们将出现频率高的信息放在离根节点近的地方，将出现频率远的信息放在离根节点远的地方，这样的话，能够很有效地提高信息查找的效率。所以哈夫曼树也叫最优查找树。
其他具体的用法还有很多，但是无一例外的是，所有的用法都是基于哈夫曼树本身的性质出发的应用。（这里也存个坑等待拓展）。

1.3.2 哈夫曼树的结构体

哈夫曼树的顺序存储结构

课本中关于哈夫曼树的顺序存储结构的设计如下：

typedef struct {
	char data;  //结点值
	double weight;  //权重
	int parent;  //双亲结点的位置
	int lchild;  //左孩子结点
	int rchild;  //右孩子结点
}HTNode;

这个是哈夫曼树顺序存储结构单个结点的结构体定义，对于整颗哈夫曼树的话，只需要知道构成哈夫曼树的结点个数就可以通过结构体数组的方式来构建哈夫曼树。
由于哈夫曼树没有度为1的结点，只有二分支结点和叶子结点，而二叉树又满足n0=n2+1，因此只需要知道叶子结点的个数 （n0） 就能知道哈夫曼树的结点的个数 (n = 2*n0-1) 了。

哈夫曼树的链式存储结构（可选）

1.3.3 哈夫曼树构建及哈夫曼编码

哈夫曼树的构建：

思路：
- 首先要先明确一下，这里建哈夫曼树的基础是，叶子节点的权重数据已经被载入哈夫曼树后，才开始哈夫曼树的构建。
- 哈夫曼树的构建，首先要对孩子指针和双亲指针进行初始化赋值，赋值为-1，代表空指针。
- 接着就是要要还没有建树的叶子节点中去寻找权值最小的两个结点，用这两个结点来建树。该算法的算法基础是在一堆数中寻找这堆数的最小数和次小数。
- 找到权值最小的两个结点后，就是创建新结点作为新树的根节点，并修改根子结点分别的亲子关系的指针，大致分为三步：1. 权重赋值 2.双亲认子 3.子认双亲。
代码展示：

void CreateHTree(HTree& T,int n)//建哈夫曼树
{
	int i, k;
	int lnode, rnode;//最小权重的两个结点的位置
	double min1, min2;//两个最小的权重的值

	//先将所有结点相关域置初值为-1
	for (i = 0; i < 2*n - 1; i++)
	{
		T[i].parent = T[i].lchild = T[i].rchild = -1;
	}

	//构造哈夫曼树的其他 n-1 个结点并完善好亲子关系。
	for (i = n; i <= 2 * n - 2; i++)
	{
		min1 = min2 = 1000000;//给大数是为了确保初始值比给出的权值都大
		lnode = rnode = -1;
		//查找权值最小的两个结点
		//算法是在数组中找最小值和次小值
		for (k = 0; k <= i - 1; k++)
		{
			//只在还没建树的结点中找元素来建树
			if (T[k].parent == -1)
			{
				if (T[k].weight < min1)
				{
					min2 = min1, rnode = lnode;
					min1 = T[k].weight, lnode = k;
				}
				else if (T[k].weight < min2)
				{
					min2 = T[k].weight, rnode = k;
				}
			}
		}
		T[i].weight = T[lnode].weight + T[rnode].weight;//赋权值
		T[i].lchild = lnode, T[i].rchild = rnode;//双亲认子
		T[lnode].parent = T[rnode].parent = i;//子认双亲
	}
}

哈夫曼编码：

以课堂派测试题目为例：
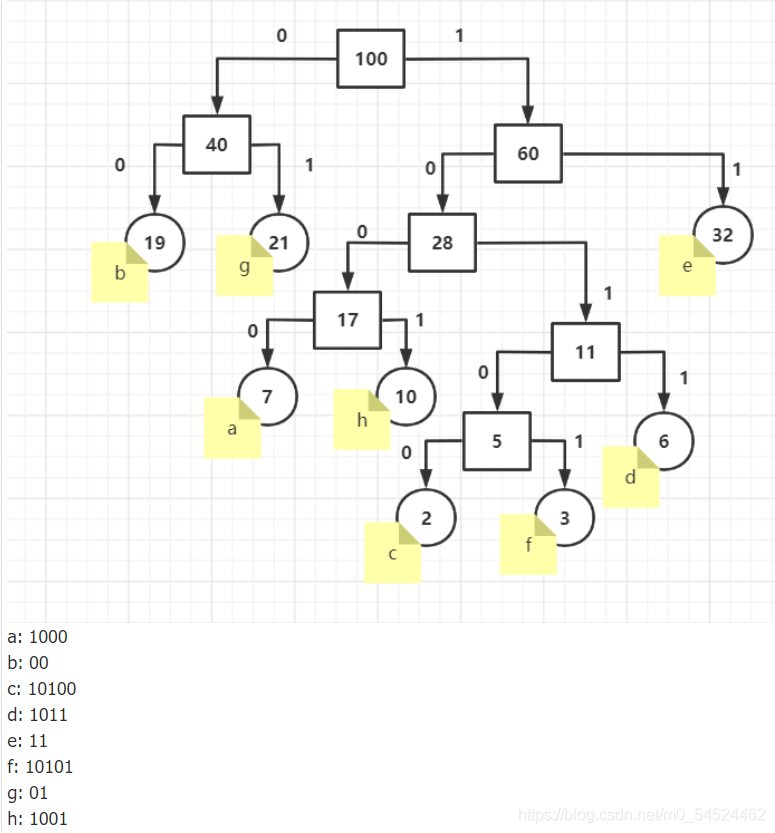
构造哈夫曼树及哈夫曼编码的步骤：

首先，先确认好每个叶子结点以及他们所对应的权值；
然后，每次选择权值序列中权值最小的两个值，令权值小的结点为左子树，权值大的结点为右子树，再以他们的权值和为该子树的根节点数据建一个子树。

因为哈夫曼树这样建树的特点，所以哈夫曼树不会有度为一的结点，只会有二分支结点和叶子结点，并且被一起选出来的这两个值（如果他们是叶子节点的话）在哈夫曼编码上的特性也会体现为，这两个结点信息的编码除了最后一个数字不同外，其他前缀数字相同。

每次创建好一个子树后，就把从权值序列中拿出的数据剔除，并把创建好的新子树的根节点的值加入序列。
按这样的逻辑不断从序列中取数建树，知道最后当序列存在的数值只剩一个时，当下建好的树就是给定序列的哈夫曼树。
然后就是进行哈夫曼编码，统一的标准是另左分支为0，右分支为1，这样从根节点开始到该叶子结点，所走过的路径按走过的顺序将数据按顺序排列得到的二进制编码，就是叶子结点所对应的元素的哈夫曼编码。（什么叫走过地顺序呢？就是从根节点到叶子结点的顺序！）

但是这里要注意一个陷阱！虽然这种方法是构建哈夫曼树最为简单的方法，但是并不是说哈夫曼树就只有这种构造方法！这里需要注意的是：WPL是唯一的，但是哈夫曼树不唯一。
我们拿图说话：
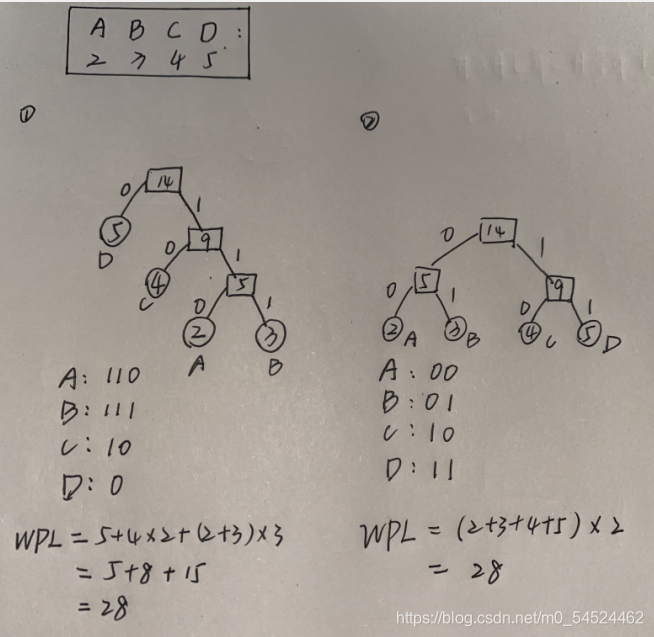
对于当下这个特定序列，两种树的WPL一致，左图是传统方法做出来的哈夫曼树，而右图是WPL刚好等于哈夫曼树的WPL的该序列的一种树，那这种情况下，当然这棵树也可以被称为这个序列的哈夫曼树啦，而它的树的结构不同，哈夫曼编码也就自然不同了，但是不能质疑的一点是，它依然是正确的哈夫曼树。
所以对于某一特定的序列它构成的树的最小的WPL是唯一的，但是它的哈夫曼树不唯一！
(可选) 哈夫曼树代码设计（可以参考链式设计方法。）
- 暂时保留位置，待补充内容。
相关补充--关于哈夫曼树的排序有需要去了解的有：
- 快速排序和堆排序。
- 关于堆排序在STL有一个专门的库叫优先队列库---priority queue.
- （这里也存个坑等待拓展）。

1.4 并查集

什么是并查集：

当给出一个两个元素的一个无序对（a,b）时，如果要求合并 a 和 b 所在的集合，那就需要反复查找某个元素所在的集合。于是就有了“并”“查”“集”的概念。并查集是含有若干个分离集合所构成的大集合。顾名思义，并查集的目的是根据某些给定的条件合并两个分离的集合，而要合并之前，必然要根据这个给定的特定条件进行反复的查找。

那么问题来了，为什么需要并查集呢？并查集解决什么问题，优势在哪里？

从数学的抽象思维来说，并查集能解决的是等价类问题，并且能高效求解等价类问题，这是并查集的优势。
那么什么是等价类问题呢：对于集合S中的关系R，若具有自反、对称和传递性，则R是一个等价关系。
怎么理解这三个性质呢，我们举个亲戚关系来说趴：假设A和B存在亲戚关系，1. 那首先的首先，要先确保A是A，B是B，不能A是B，或者B是A，这就叫自反性。2. A是B的亲戚，那B也是A的亲戚，这就叫做对称性。3. 假设这时候又出现了C，A和C也是亲戚关系，结合已知的A和B存在亲戚关系，我们能够得到B和C存在亲戚关系，这就叫传递性。
所以显然亲戚关系是一种等价关系，探讨亲戚关系的问题就是等价类问题，就可以用并查集来解决。
那用并查集解决这些问题高效在什么地方呢？就让我们从具体的代码层面去分析趴。

并查集的结构体、查找、合并操作的具体实现。

并查集的数据结构常用的有三种实现---数组实现、链表实现、树实现。
以顺序树为例：
- 先交代一些顺序树的特点，顺序树的每个元素用他们所对应的下标来表示，顺序树用根节点元素所对应的下标来表示。

2.1 并查集基于顺序树的结构体：

typedef struct node {
	int data;  //结点对应元素的编号 
	int rank;  //结点对应的秩（子树高度）
	int parent;  //结点对应的双亲下标
}UFSTree;  //并查集树的结点类型

2.2 顺序树并查集的初始化：

void MAKE_SET(UFSTree* t, int n)
{
	int i;
	for (i = 0; i < n; i++)
	{
		t[i].data = i;
		t[i].rank = 0;//秩初始化为0
		t[i].parent = i;
	}
}

2.3 顺序树并查集的查找：

类似顺序结构存储的树找祖先的过程。

int FIND_SET(UFSTree* t, int x)//在x所属的集合
{
	//x是某个元素对应的编号。
	if (x != t[x].parent)
	{
		return FIND_SET(t, t[x].parent);
	}
	//相等的时候代表找到树的根结点了，也就算找到所属集合；
	//在顺序结构中，我们用根节点元素作为代表元素来表示一个树。
	//可以用根节点元素的下标来定位根节点，以及其表示的树。
	else
	{
		return x;
	}
}

对于n个元素，构成的分离集合树的高度最高为log(2,n)，所以该算法的时间复杂度为O( log(2,n) )。
2.4 顺序树并查集的合并：
合并的过程依靠的是比较两个分离集合树的高度，通过将高度更小的树作为高度较高的树的子树，从而实现两个树（集合）的合并。操作很简单，只需要将高度更低的树的根指向更高树的根就行，但是对于高度相等的两个数来说不同，不过只需要将一棵树的根指向另一颗的根，然后再将被指向的树的根的秩加一就行。

void UNION(UFSTree* t, int x, int y)//合并元素x所在的集合和元素y所在的集合
{
	//合并前要先找集合
	x = FIND_SET(t, x);
	y = FIND_SET(t, y);
    //找完之后要合并
	if (t[x].rank > t[y].rank)
	{
		t[y].parent = x;
	}
	else
	{
		t[x].parent = y;
		if (t[x].rank == t[y].rank)
		{
			t[y].rank++;
		}
	}
}

1.5 森林、树、二叉树的转换：

详细见森林、树、二叉树的转换

引用自百度经验。

1.6.谈谈你对树的认识及学习体会。

最初的认识和体会请见开头的引入部分。
除了开头讲到的关于树中递归和分治思想会被广泛使用到的这一点之外，其实还应该谈谈另一种思想，起初由于首映效应，只看到递归分治思想对数的问题处理的方便快捷，但却忽略了在学习树以前，我们一直学习的那种线性的一维的思想，他也并非就失去了闪光点。从树的层次遍历就可以看出，对一些树的问题的探究，采用线性的思维也有它独到的地方。这时我们才豁然开朗，非线性结构的特点在于它的维度是二维的，也就是说它有两个方向的投影，很显然，递归思想适用于树在纵向方向投影的问题，而对于横向方向投影的问题，也固然有它自己适合的思想，没错就是把非线性拆成一层一层的线性来看的线性思想，更具体的来说，它借用的结构基础是队列。
在这个维度的基础上去看问题的话，我们不妨把递归再深挖一下，递归底层的结构基础是什么呢？没错递归底层的结构基础是栈！于是我们站在树的这种非线性思维的角度去做两个方向的投影，得到的结构基础竟然是我们在线性结构当中 栈和队列 这两个基本的数据结构。

所以这里可以看出,再困难的问题本质上对其的处理都是划分到更简单的方向上去处理。在这里我们不妨猜想，其实无论问题的维度是多少个维度，最终的最终，我们都是对问题进行逻辑抽象，直到最后拆分到一维线性角度来处理。

继续对栈和队列进行深度的思考，栈和队列这两个结构本身又代表了些什么思想呢？借用栈和队列当中的迷宫问题我们会发现，其实栈代表的是纵向方向的一种投影，是深度思维，而队列代表的是一种横向方向的一种投影，是广度思维， 于是有：
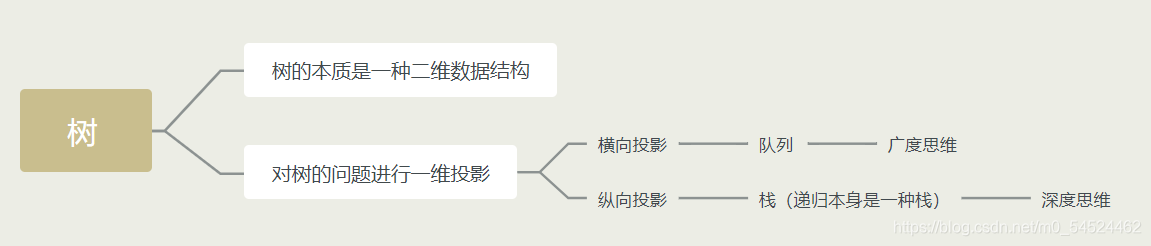
回归到树的问题的具体应用的话，俺觉得由于某些概率上的巧合，树的这一块在代码层面上我的训练量其实远远不够，所以相对来说我觉得我的实践远远不够，还应该去拓展很多内容，无论是多叉树的孩子兄弟链这块，还是线索二叉树，哈夫曼树，并查集，以及他们在STL库中相应的部分，其实都值得去多了解了解。

2.PTA实验作业（4分）

输出二叉树的每层结点
 目录树的代码

2.1 输出二叉树的每层结点

在这里插入图片描述

2.1.1 解题思路及伪代码

解题思路：
- 本题的数据结构采用二叉链树。
- 首先是对输入的顺序存储的前序遍历序列进行建树，前面的前序建树部分已经进行过详细的解释，这里不再进行赘述。
- 重点讲我实现层序遍历并按从左到右，从上到下的顺序进行一层一层结点输出的思路。
- 这题是修改了树的结构体定义，加入了level的变量，在建完树后另外用一个函数对树的每个结点所在的层数进行标记；
- 然后在层次遍历的时候，按层序遍历的思路借用一个队列对树进行一层一层的扫描，专门用一个变量来记录当前已经扫描到的层数， 每次要输出元素之前就拿即将要输出的元素的level值和当前所在的层数进行比较，如果发现不一致就立刻换行并改变当前层数变量的值并立刻输出当前所在的层数，然后再输出当前出队元素，如此不断进行输出，直到队列为空，代表整棵树层序遍历结束，同时输出完毕。
- 另外要注意的是：和层次遍历一样，有元素出队后，如果它的孩子不为空，就让它的孩子入队。
伪代码：

//先序顺序序列建树；
//递归先序遍历二叉树，给每个结点标记level；

//按层输出结点：
根节点入队
while(队不空)
{
	取队首元素另存；
	if(队首结点的层数==cur_level)//cur_level默认为1
	      if(cur_level == 1)  打印“ 1: ”
	      输出结点元素;
	      队首元素出队;
	      孩子不空孩子入队；
   	else
   	      换行；cur_level变值。
   	      cout << "cur_level:";
   	      输出结点元素;
   	      队首元素出队;
	      孩子不空孩子入队；
}

2.1.2 总结解题所用的知识点

用到了根据顺序存储结构的先序遍历序列来建树的建树方法；
用到了求树的高度的算法来给每个结点标记层数；
用到了二叉树的层次遍历的方法。
使用了C++STL库中的queue容器。

2.2 目录树

题目截图：

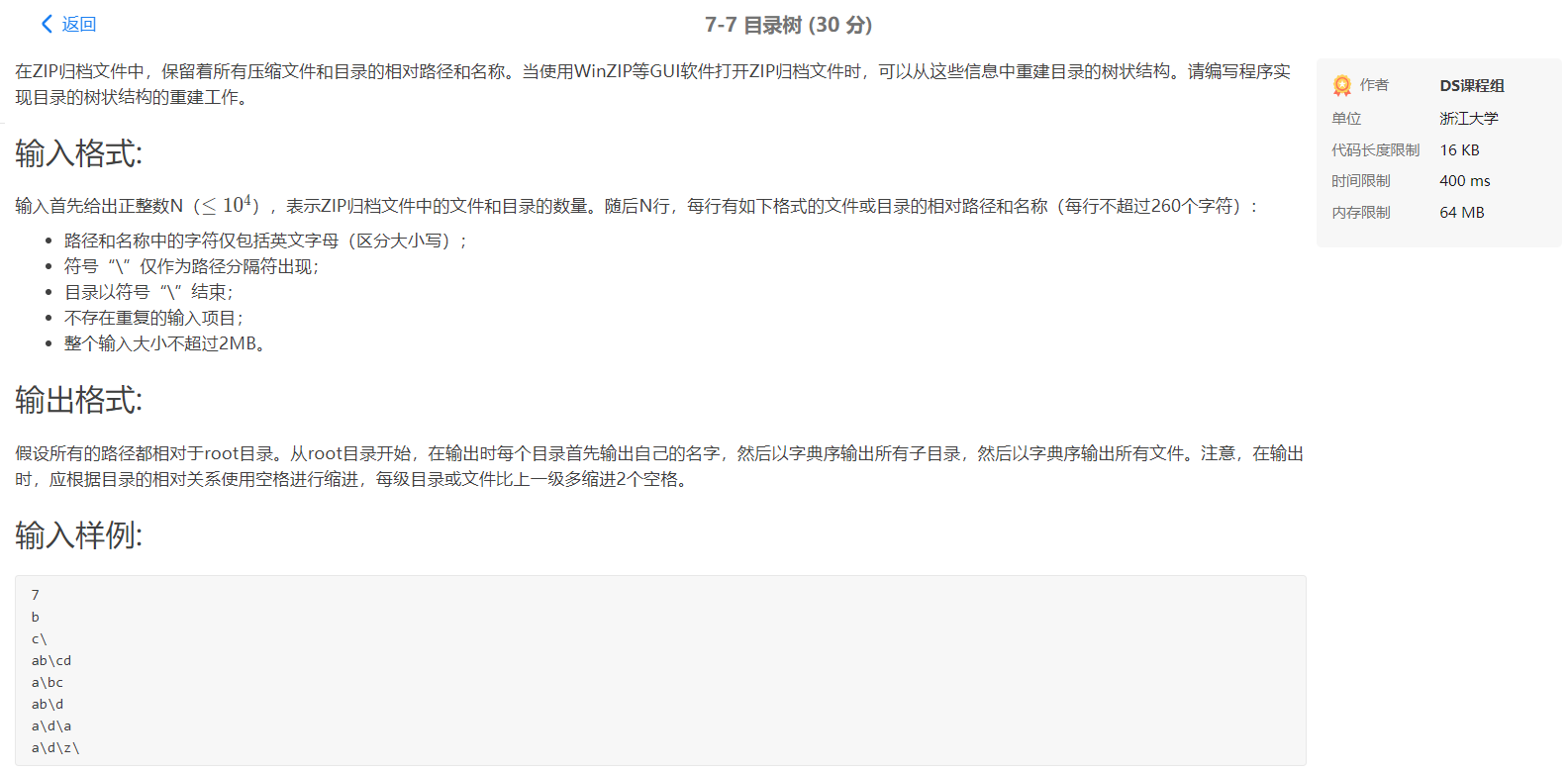
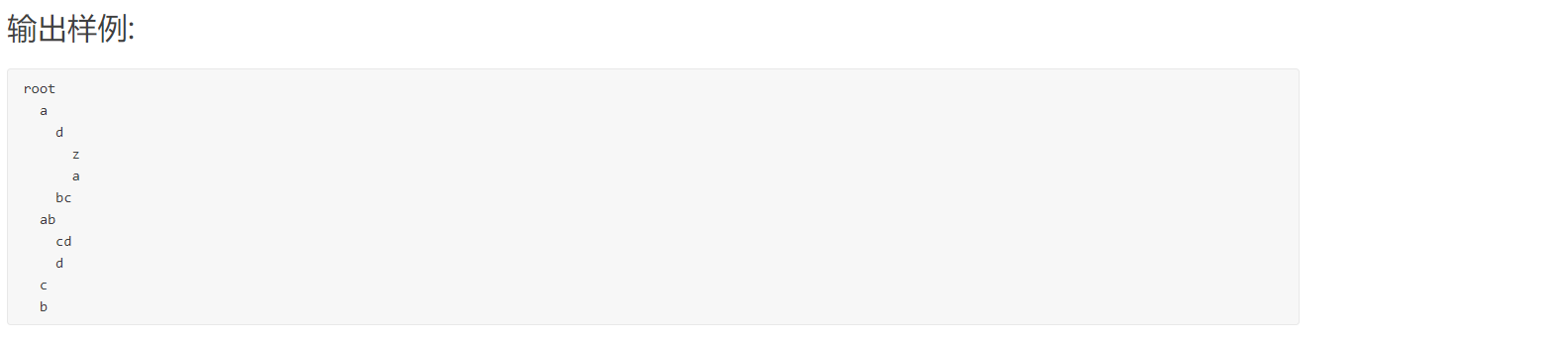
2.2.1 解题思路及伪代码

解题框架和具体细节：
<1> 大框架：

[数据读入]首先要用借用一个循环一行一行读入字符串；
[数据处理]对数据进行一行一行的处理，拆分出各个目
录和文件；
[简单的建树]对处理好的数据进行合理的建树结点；
[复杂的插入]根据各种不同的情况将建好的树结点
插入目录树的合适的位置；
[有格式的输出]根据格式要求实现具体输出。
<2> 细节讨论：
[数据处理]:
- 因为输入的每行数据都有一个特点是：是按先目录后文件的顺序来输入的，
  并且目录有一个鲜明的特点是'\'结尾。
- 接着就是先用循环把目录元素先处理了，如果末尾元素不是以'\'结尾
  那代表最后一个元素是文件元素，要另外处理。
- 这里有一个要点对'\'的查找要求从前一个找到的位置开始找，所以要用find的
  其他形式！
- 在数据处理的时候就把文件和目录分开的话，对后面的建树也有一定的好处。
[简单的建树]与[复杂的插入]:
- 首先，由于是一行一行读取，一层一层建，所以每一层要插入之前，
  都需要知道前一层插入的那个结点到底在哪里，所以需要有一个指针来存
  放上次建的那个树插入到哪里去了。
- 其次简单的建树就是对树进行初始化罢了，只有一个需要区分的地方，
  就是区分这个数存的元素，到底是不是目录，可以在函数加个参数来判断区
  分。
- 开始对不同的插入的情况进行分析：

1.1 插入作为孩子（头插法）

1）如果当前结点没有第一个孩子，则直接插入作为第一个孩子结点。
2）如果当前结点有第一个孩子，则是否需要更改孩子：
<1假设要插入的对象是目录时：
  1> 如果第一个孩子为文件，那直接头插，修改首孩为新结点。
  2> 如果第一个孩子为目录，但是值比新节点大（字典序靠后），也更新新结点为首孩结点。
  3> 如果第一个孩子为目录，但是值与新节点相等（字典序相等），那就让当前结点指向它的第一个孩子结点，然后删除新建的newNode，退出返回。
<2假设要插入的对象是文件时：
  1> 如果第一个孩子为文件，但是值与新节点相等（字典序相等）那就让当前结点指向它的第一个孩子结点，然后删除新建的newNode，退出返回。

1.2 插入作为兄弟(插入排序)

先找后插就完事了。
1）如果当前结点没有兄弟，则直接插入为兄弟。
2）如果当前结点有兄弟：

// 先查找
<1假设要插入的对象是目录时:
while（值比我大 && 类型相同） 往下找
跳出时的位置就是目录插入的位置；
<2假设要插入的对象是文件时:
while（指针不空）
  if （值比我大 && 类型相同）找到了位置

* 这两步可以放在一个循环里面，把文件还是目录的分支放循环里面讨论，
找到了位置后要提前退出！
//后插入（ptr是插入位置的前驱指针）
1>如果到表尾了（ptr->brother == NULL）直接尾插新结点
2>其他情况，先继承原来的brother关系，再修改ptr->brother = 新结点

一些具体代码的实现的抉择：

为什么取消先完成字符串的读取再另外在建树中遍历字符串进行逐行的操作呢？
- 因为完全可以直接在建树的函数当中进行边读取边一行一行处理数据。
- 这样做的话可以省掉一个循环，时间复杂度能减少很多。
  （尤其是在数据量变大的时候）
对子串进行拆分的方法：
- 可以用string类本身自带的内联函数来做子串分割处理。
  - find函数和substr函数；
- “可以借用字符数组的思维加上字符串可以由字符相加来构建这一点来处理数据”
  这个想法也实现。
- 对数据的处理本质上是各种对子串的分割操作的实现,毕竟我们所讲的大部分的
  对数据的处理，都是一种对字符串的处理。

2.2.2 总结解题所用的知识点

多叉树的孩子兄弟链结构：定义、先序遍历、以及求树的高度。
链表的头插法和插入排序的内容。
难在分析使用头插或者插入排序的分支判断条件上，就是很多具体细节的处理非常麻烦。
更难在，如何调整LastTNode这个跟踪建树的指针能出现在正确的需要建树的位置。

当前还没有完成但是有了大概的代码需要时间慢慢调试。
- 目前达到的进度：
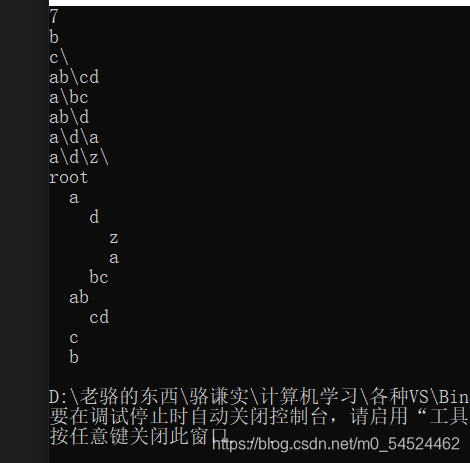
- 建树代码存在错误:
  - 问题在于，如果下一层输入的信息中包括的目录是前面已经建好的目录，那如何把跟踪上一层的指针，合适地定位到它该存在的位置。

3.阅读代码（0--1分）

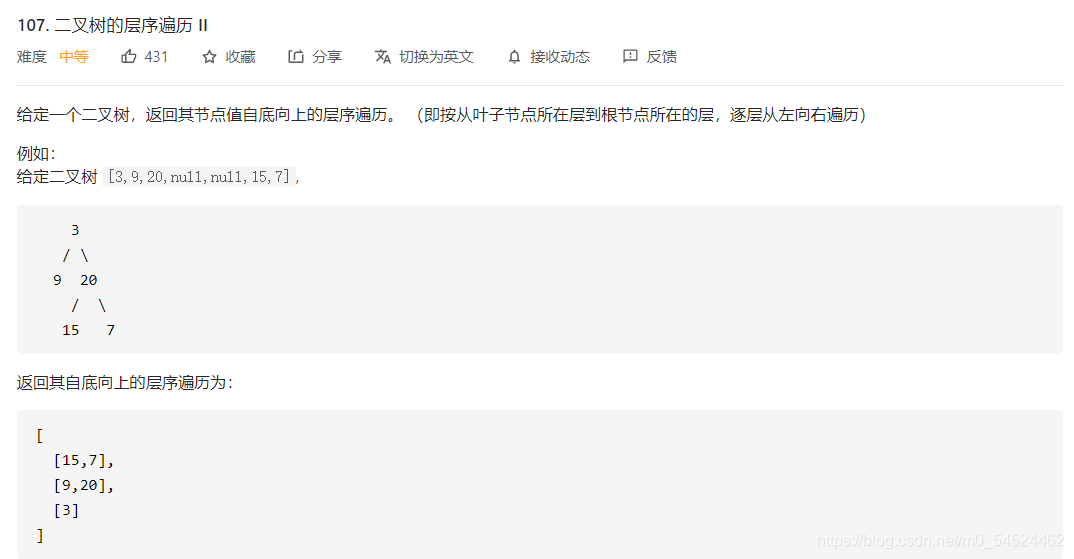
3.1 题目及解题代码

选题的原因：因为我们在PTA有做过输出树的每层结点的题目，这个题目在上文已经有描述过，详细可以看上文。然后算是同一种思维的不同方向的应用，所以选这道题来进行横向对比。
leetcode官方解题代码：

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        auto levelOrder = vector<vector<int>>();
        if (!root) {
            return levelOrder;
        }
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            auto level = vector<int>();
            int size = q.size();
            for (int i = 0; i < size; ++i) {
                auto node = q.front();
                q.pop();
                level.push_back(node->val);
                if (node->left) {
                    q.push(node->left);
                }
                if (node->right) {
                    q.push(node->right);
                }
            }
            levelOrder.push_back(level);
        }
        reverse(levelOrder.begin(), levelOrder.end());
        return levelOrder;
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal-ii/solution/er-cha-shu-de-ceng-ci-bian-li-ii-by-leetcode-solut/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

3.2 该题的设计思路及伪代码

先看看作者的思路：
- 树的层次遍历可以使用广度优先搜索实现。从根节点开始搜索，每次遍历同一层的全部节点，使用一个列表存储该层的节点值。
- 如果要求从上到下输出每一层的节点值，做法是很直观的，在遍历完一层节点之后，将存储该层节点值的列表添加到结果列表的尾部。 这道题要求从下到上输出每一层的节点值，只要对上述操作稍作修改即可：在遍历完一层节点之后，将存储该层节点值的列表添加到结果列表的头部。
- 为了降低在结果列表的头部添加一层节点值的列表的时间复杂度，结果列表可以使用链表的结构，在链表头部添加一层节点值的列表的时间复杂度是 O(1)O(1)。在 Java 中，由于我们需要返回的 List 是一个接口，这里可以使用链表实现；而 C++ 或 Python 中，我们需要返回一个 vector 或 list，它不方便在头部插入元素（会增加时间开销），所以我们可以先用尾部插入的方法得到从上到下的层次遍历列表，然后再进行反转。
根据作者的思路我提炼出来的伪代码：

//树的结构依然是使用二叉链树
//列表的容器用vector<vector<int>>,可以想象成有一条表头链，这个链的每个表头结点的元素又是一条链，这条内层链的每个结点的元素是整形数据。

//先让根节点入队列
while(队不空)
{
	建每层的数据链 vector<int>
	保存该层的长度也就是队列长度（第一层只有根节点所以队列长度为1）
	while(队列内还有该层元素)
	{
		取队首元素；
		将队首元素的的值尾插入数据链；
		队首元素出队；
		如果队首元素的孩子不空，让孩子入队；
	}
	将数据链尾插入数据链表中（因为vector不方便头插）；
}
尾插完再翻转数据链表得到的效果和头插一样。

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal-ii/solution/er-cha-shu-de-ceng-ci-bian-li-ii-by-leetcode-solut/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：虽然文中使用了两层循环，但是整个大循环的本质，是把让树中的每个结点入队并出队，所以循环的总语句频度取决于树的结点个数，如果设树的结点个数为n,则时间复杂度为O(n)。
空间复杂度：空间复杂度取决于队列的开销，而事实上队列的长度不会超过二叉树的结点总个数，如果二叉树有n个结点，那它的空间复杂度为O(n)。

3.3 分析该题目解题优势及难点。

先说说这道题在知识体系上能学习些什么吧，首先是为变量动态申请内存的操作，我们看到文中使用的是auto而不是new,也就是说在面向对象编程的过程中，我们对一个变量进行动态内存申请更多使用auto,其次，知道了容器的定义可以套娃使用----vector<vector<int>>如果必要的话，另外学习一下vector容器的功能--reverse(levelOrder.begin(), levelOrder.end()),里面的begin(),end(),也是vector的功能，取开头元素和结尾元素。
在说说这道题目的优势：
- 首先不同的一点是，它并不是直接将数据输出，而是用了一个链表来存储数据，由于有了这个临时的数据储存的结构，使得代码的容错率更高，因为给了我一个可以处理数据的中转站，无论它要求数据的输出方试是从上到下，还是从下到上，我都只需要操作链表来变更输出，而不需要去更改层次遍历的内容。（如果是上文我自己实现的代码就没办法通过简单更改来满足这道题目的要求，但是这个做法却可以，并且这道题的解法只需要把翻转链表那一步去掉，就可以实现从上到下的每层结点输出）
- 这告诉我们当我们通过遍历得到一组数据后，要先考虑用什么数据结构去合理存储，才能适应不同的输出要求，而不是在遍历的过程中直接考虑输出，这样的代码实用范围太局限了。
- 另外一个点是，它引入队列长度这个量来控制树的每层遍历，有了这个层次的区分，当我们需要操作的对象是一层一层地去看这个二叉树的时候，就会方便很多，比如求二叉树的宽度这个问题就需要用到这个知识点。（详细请看上文层次遍历的举例。）
难点在于1、想到用链表来存储层次遍历的数据，2、以及在已有容器有限制的情况下，想到用尾插加翻转来替代头插。
要学习面向对象的编程思想。

posted @ 2021-05-01 23:01 嘟嘟勒个嘟阅读(255) 评论(0) 编辑收藏举报

刷新页面返回顶部

数据结构——树

0.PTA得分截图

1.本周学习总结（5分）

引入——树的递归和分治思想。

(递归与分治思想的例题)-----6-3 求二叉树高度 (20 分)

1.0 树的基本概念和性质

1.0.1 树中的基本术语：

1.0.1 树中的基本性质：

1.1 二叉树结构

1.1.1 二叉树的两种存储结构

1.1.2 二叉树的构造

1.1.3 二叉树的遍历

1.1.4 线索二叉树

1.1.5 二叉树的应用--表达式树

1.2 多叉树结构

1.2.1 多叉树结构

1.2.2 多叉树遍历

1.3 哈夫曼树

1.3.1 哈夫曼树定义

1.3.2 哈夫曼树的结构体

1.3.3 哈夫曼树构建及哈夫曼编码

1.4 并查集

1.5 森林、树、二叉树的转换：

1.6.谈谈你对树的认识及学习体会。

2.PTA实验作业（4分）

2.1 输出二叉树的每层结点

2.1.1 解题思路及伪代码

2.1.2 总结解题所用的知识点

2.2 目录树

2.2.1 解题思路及伪代码

一些具体代码的实现的抉择：

2.2.2 总结解题所用的知识点

3.阅读代码（0--1分）

3.1 题目及解题代码

3.2 该题的设计思路及伪代码

3.3 分析该题目解题优势及难点。

公告