the summury of array in C.
| 这个作业属于哪个班级 |
| ---- | ---- | ---- |
| 这个作业的地址 |
| 这个作业的目标 | 学习数组相关内容 |
| 姓名 | 骆锟宏 |
~~段首鸣谢好久没有整整个了。
- 感谢这篇文章的作者,这里引用过来作为拓展资料。浅谈排序算法
0. PTA上数组题目的截图:
数组:

字符数组:

1. 本章学习总结:
1.1 数组中查找的方法
1.1.1 顺序查找法:
- 以PTA题目查找整数为例:核心思想就是,遍历数组,然后让数组中的每一个数与目的数进行比较,如果存在相同的情况,那就记下数组当中该数的下标,
记下下标也就算是找到了该数。
//顺序查找法,实质是遍历数组一一比较;
for (Index = 0; Index < N; Index++)
{
if (a[Index] == X)
{
flag = 1;//此时表示已经找到
loc = Index;
}
}
//为了输出方便一般会另设一个标记变量来标记找到与否。
1.1.2 二分查找法:
- 以课堂派的测试题为例:核心思想就是,让这个数不断和已知数组中的中间数进行比较,每次比较过后缩减一半的范围,直到最后无法再缩减,找到数字,或者
数组中不存在该数字,找不到。
//假设存在数组a[],find表示要找的数,left表示左界的下标,right表示右界的下标。
while (left <= right)
//这种情况下相等的情况也要考虑,而且往往找到的情况是left = right = middle的情况!
{
middle = (left + right) / 2;
if (find == a[middle])
{
printf("这个数是第%d个数", middle + 1);
break;
}
else if (find > a[middle])
{
left = middle + 1;
}
else
{
right = middle - 1;
}
}
if (left > right)
{
printf("找不到这个数");
}
1.2 数组中插入数据的方法
- 数组当中插入数据的办法:往往是先找到需要插入的位置,然后从最后一个数字开始,
慢慢地把数字一个一个,往后移动,最后空出插入的目的位置给需要插入的数字。 - 但是要求是,数组的长度要足够长,必须要大于已经存在的数字和想要插入的数字的个数之和。
- 如果要插入多个数字,只需要对要点一进行重复操作就行。
以PTA中简化的插入方式这道题为例可知:
//判断代码可以插入的位置;
for (count = 0; count < numbN; count++)
{
if (numbX > a[count])
{
loc = count + 1;
}
}
//将数组中从这个位置开始向后移;
for (countChange = numbN; countChange > loc; countChange--)
{
a[countChange] = a[countChange - 1];
}
a[loc] = numbX;
1.3 数组中删除数据的方法
1.3.1 简单地删除某几个数:
- 一种比较常见的方法就是 重构数组,那就是先找到需要删除的那个数的位置,然后从这个数的下一位开始,
逐个往前移动,直接覆盖前面的数据,最后输出的时候记得数组长度进行相应的减少即可。 - 如果需要多次删除的话,那就需要多次重构数组。
- 以PTA题目数组元素的删除为例:
scanf("%d", &k);//这里的k表示删除的次数;
for (i = 0; i < k; i++)
{
scanf("%d", &order);//order表示想删除的数的位置;
for (j = order - 1; j < n; j++)
{
array[j] = array[j + 1];
}
n--;
}
1.4 数组中目前学到的排序方法及其主要思路
1.4.1 选择排序法:
- 主要思路:选择排序法的主要思路是先找出一段范围内的最值(最大值和最小值都可以),然后将他们先
放在一边(习惯上统一先放左边,所以我们以此方法为例),也就是说找到最值的位置后,让最值的数的位置
和最左边的数的位置进行交换,让最左边的空间存放的是最值,然后再在除去左边的值的剩下的值的范围中一
次一次不断地重复前面的操作直到倒二个数,这是第一层循环的终点,第二层循环的终点一般都是数组长度,
但是它的初值在不断地从第二个数组元素的下标开始直到数组长度停止,最终如果排序完整个数组的话,往往可
以得到一个从小到大或者从大到小排列的数组。其它情况根据具体情况去改变循环条件去具体分析。 - 以PTA的题目选择法排序为例:
//数据表达
unsigned int n;
int a[11];//数组a;
int Index = 0;//控制数组输入的下标;
int count = 0;//计数当前刷过几遍;
int temp;//用于存储暂时的变量;
int bigIndex;//用来表示更大数的下标;
//选择法排序1;
for (count = 0; count < n - 1; count++)
{
bigIndex = count;//表示最大数的下标 并在每一轮先表示那一轮内循环的第一个数;
for (Index = count; Index < n - 1; Index++)
{
if (a[bigIndex] < a[Index + 1])//以本循环内的第一个数为起始点,不断与下一个数进行大小比较;
{
bigIndex = Index + 1;//用一个下标变量来定位最大的那个数;
}
else;
}
//将最大数交换到当前的第一个数的位置来,然后把当前第一个数的换到原本最大数的那个位置;
temp = a[count];
a[count] = a[bigIndex];
a[bigIndex] = temp;
}
//细心的读者会发现,哎呀怎么给的代码和思路中描述的不太一样,其实他们表达的本质都是一样的,之所以
会有循环条件控制的这两种不同的写法,最主要的目的还是为了去避免数组下标的溢出。
- 非常非常非常需要注意的一点就是,在数组问题当中循环上下限的设置,不仅仅要满足逻辑上效果的满足,更
重要的是,它还要保障跑的过程中,每一个作为数组下标的量或表达式值的结果都不能越界!!
所以我们再放一种写法它也能过:
//选择法排序2;
for (count = 0; count < n - 1; count++)
{
bigIndex = count;//表示最大数的下标再每一轮先表示那一轮内循环的第一个数;
for (Index = count + 1 ; Index < n; Index++)
{
if (a[bigIndex] < a[Index])//以本循环内的第一个数为起始点,不断与下一个数进行大小比较;
{
bigIndex = Index;//用一个下标变量来定位最大的那个数;
}
else;
}
//将最大数交换到当前的第一个数的位置来,然后把当前第一个数的换到原本最大数的那个位置;
temp = a[count];
a[count] = a[bigIndex];
a[bigIndex] = temp;
}
1.4.2 冒泡排序法:
- 实验思路:冒泡排序法的思路是一种临近元素两两满足条件不断交换的思路,同样设置两层循环,外层循环控制
的范围是从数组中的第一个元素开始,不断得去提取元素,直到提取到最后一个元素,而内层循环控制的是每次交换
的一个范围,它的每次循环的范围会向一个方向缩减,缩减的数量就是已经排序完成,成功冒泡的元素的个数(常
见的是往右边冒泡),然后内循环的右界不断缩减直到为零,而左界保持不变一直都是第一个元素的下标。通过这
样的过程,如果最后完全排序完成的话,也可以得到一个从小到大排序或者从大到小排序的数组,具体情形自己分
析。 - 具体的实例代码可以参考PTA的题目冒泡排序法:
//数据表达
unsigned long int N;
unsigned long int K;
int a[101];//数组a;
int Index = 0;//控制数组的下标;
int count = 0;//计数当前刷过几遍;
int temp;//用于存储暂时的变量;
//冒泡法排序;
for (count = 0; count < K ; count++)//这里表示一共做冒泡法的轮数,K的表达形式与count的初值有关!
{
for (Index = 0; Index < N - count-1; Index++)//这里面的 N - count-1 很重要!!!-1是保证数组下标不越界;
{
if (a[Index] > a[Index + 1])
{
temp = a[Index + 1]; a[Index + 1] = a[Index]; a[Index] = temp;//做交换;
//要记住交换的 传递性 写法!!
//这样写一是可以的: temp = a[Index]; a[Index] = a[Index + 1]; a[Index] = temp;
//记住一个看起来的特点那便是:首 尾 顶 真 !
}
}
}
- 这里就分析一下选择排序法和冒泡排序法的区别:
**你会发现,选择排序法的交换是放在第一层循环中,而冒泡排序法是放在第二层循环中,所以相对来说
选择排序法的代码的结构性会比冒泡排序法的更好,效率会更高。 - 更深入的理解请访问该文章:浅谈排序算法
1.5 数组做枚举用法及其案例
- 用数组来做枚举的话,一般要求数与数之间存在一定的逻辑关系,我们通过其逻辑关系来表示他们可以省力很多。
这种情况下,一般是要先将特殊的情况另外表示出来,有规律的再用数组进行枚举表示。 - 案例如下:
PTA题目 杨辉三角:
代码如下:
#include<stdio.h>
int main()
{
int n;
int i, j;
scanf("%d", &n);
int array[9][9];
for (i = 0; i < n; i++)
{
for (j = 0; j <= i; j++)
{
if (i == j || j == 0)
{
array[i][j] = 1;
}
else
{
array[i][j] = array[i - 1][j - 1] + array[i - 1][j];
}
}
}
for (i = 0; i < n; i++)
{
for (j = 0; j <= i; j++)
{
printf("%4d", array[i][j]);
}
printf("\n");
}
return 0;
}
1.6 哈希数组用法及其案例
- 哈希数组的主要思想是用空间换时间,它巧妙地运用了数学中复合函数的思想,正好数组的下标和它对应的元素
也在某种程度上反映了一种一一对应的映射关系,所以它让一个数组去当另外一个数组的下标,让内数组对应的元素
去充当外数组的下标,不过要求的是,内数组对应的元素的取值范围要在外数组下标的有效范围之内,这同样也和数学
上复合函数的对应思路一致。 - 以PTA中有重复的数据I为例:
//这是过不了审的用了循环嵌套的做法:
int main()
{
//数据表达
int n, i, k;
int numbers[100000];
int numbers1[100000];
int count = 0;
//流程设计
//input
scanf("%d", &n);
for (i = 0; i < n; i++)
{
scanf("%d", &numbers[i]);
}
for (i = 0; i < n; i++)
{
for (k = i; k < n; k++)
{
if (numbers[i] == numbers[k])
{
count++;
}
}
}
if (count >= 2)
{
printf("YES");
}
else
{
printf("NO");
}
return 0;
}
/* 用这种方法来解决 有重复的数据I 过不了数字很大的 测试点。但是这个方法是有值得学习的地方的
那就是对数组的一种思考方式:==那就是可以通过定义两个在改变的不同变量来当作同一数组的下标使用
数组。== */
- 其实可以把数组想象成数学中的函数关系,下标就是自变量,支持 复合函数 的思想 所以也就支持数组嵌套。
//于是有了哈希数组的方法:
int main()
{
//数据表达
int n, i;
int numbers[100000];//内数组用来存放实际元素;
static int numbers1[100001];//外数组用来统计个数。
int flag = 1;
//流程设计
scanf("%d", &n);
for (i = 0; i < n; i++)
{
scanf("%d", &numbers[i]);
}
for (i = 0; i < n; i++)
{
numbers1[numbers[i]]++;
}
for (i = 0; i < n; i++)
{
if (numbers1[numbers[i]] >= 2)
{
flag = 0;
}
}
if (flag)
{
printf("NO");
}
else
{
printf("YES");
}
return 0;
}
- 值得注意的是使用了哈希数组之后,后期对外数组计数的统计,你所使用的下标也应该
是数组下标,这样才能够既解决计数统计的需要又不至于要遍历整个外数组,浪费时间。 - 要注意外数组的长度和内数组元素数据取值范围的一一对应,避免下标越界!
1.7 字符数组、字符串特点及编程注意事项
1.7.1 字符数组的输入:
- scanf类型的输入方法:支持中间没有空格的输入类型,因为一遇到空格或者回车就会立刻
停止输入。另外这种方法会自动补充字符数组的结束标志,不需要另外自己赋值。
//假设此刻有一个字符数组为a
scanf("%s",a);
//其中字符数组的变量名本身就代表首地址所以不需要 & ,其次不需要[]。
- while类型的输入:这种做法就像是把字符数组拆分成一个一个的字符,它是相当于在循环中
一个一个把字符给输入到字符数组当中,可以应对有空格或者回车的输入环境,但是缺点是,它
并不会自动补充字符数组的结束符号 '\0' (也就是 0 );所以往往需要在循环结束时在循环外
对数组的已输入元素的后一位手动赋值来封尾,这样,字符数组的输入才算成功输入。另外,输
入循环结束的条件往往需要自己设置,这个根据题目来具体分析。
//这里假设输入一串字符并用 回车 来结束输入:
while ((str[i]=getchar()) != '\n')
{
i++;
}
str[i] = '\0';
- fgets类型的输入:fgets类型的输入可以解决输入的过程中遇到空格或者换行的问题。但是fgets输入有一个特点就是,
除了字符串本身的'\0'之外,他还会在结尾多加一个'\n',所以这要求我们要申请的数组长度要比实际长度多2,以及在循环
条件的书写当中,往往要写成str[i] && str[i] != '\n',这样才算是遍历完了由fgets输入完成的字符串。
1.7.2 字符数组的函数接口设计:字符数组的数组名本身就代表了字符数组的首地址。所以在传参的时候,只需要把字
符数组名写上去就行。
1.7.3 字符串的输出:
- 可以采用循环输出的方式:
for (i = 0;str[i];i++) putchar(str[i]);
- 可以采用printf的输出方式:
printf("%s,str");
printf("%s","How are you?");
- 可以采用puts的输出方式:
puts(str);
puts("How are you?");
- puts输出完后会自动换行。
1.7.4 字符串的转换:
- 将字符串中的一串数字转换成整型的数字:
n = n*10 + (str[i] - '0')(n初值为0); - 字符串进制转换的样例(来自字符串课堂派测试):

2. PTA实验作业(7分)
2.1 判断上三角矩阵(3分)
2.1.1 伪代码
用scanf语句输入T
再在while语句(while(T--))内分别对T个矩阵进行输入;
每输入完成一个矩阵后,再接一个循环这个循环用来判断是不是上三角矩阵
if count1(row) > count2(col) 存在matrix[count1][count2] != 0
那就说明这个矩阵不是上三角矩阵 ,让flag[count3] = 1(默认flag[] = 0为是上三角);
count3用来表示待测矩阵的序数,每次 T减1,它就加1。
最后统一输出当flag[]等于0时输出YES,当flag[]等于1时输出NO。
2.1.2 代码截图
-
初始版本:(先输入后判断版本)

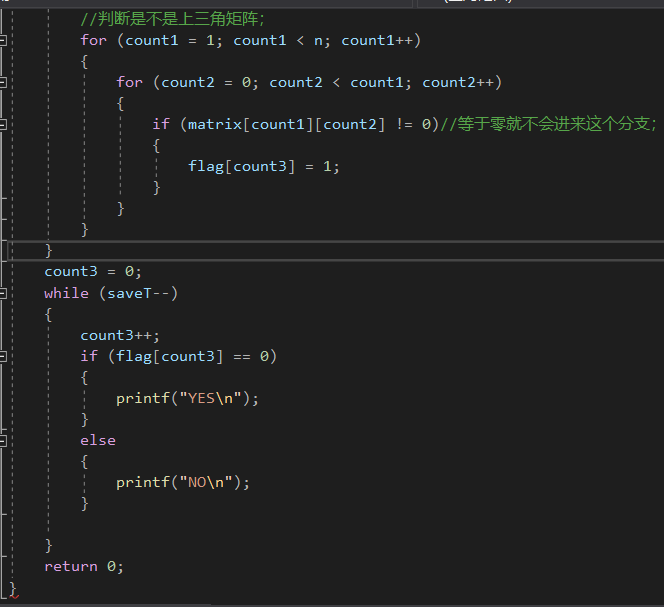
-
学习版本:(边输入边判断版本)
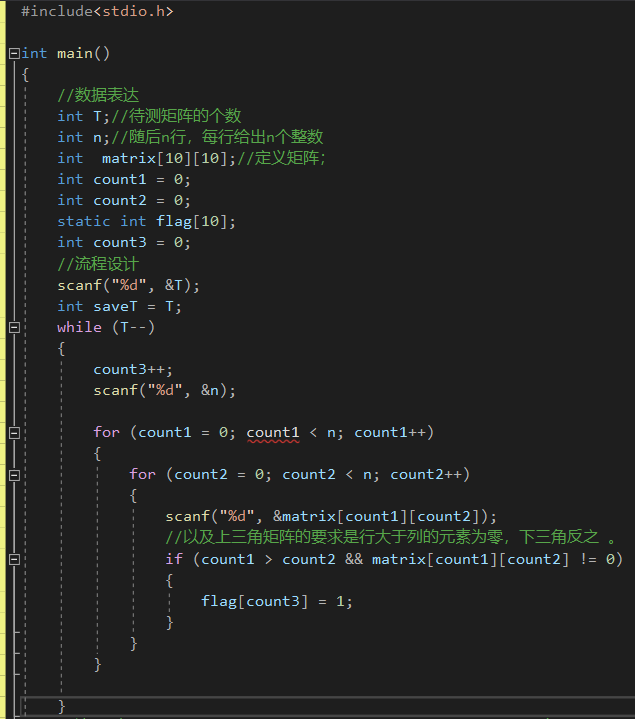

-
这里面要强调一个我的思维定势的问题,那就是不要总是要强迫得把flag = 1才当成是true,要灵活一点,对数组
的初始化,整体赋零的操作比较简单,所以可以用flag == 0来充当true的条件,灵活一点,不要太思维固化。
2.1.3 代码比较(感谢陈剑同学的大力支持!)
小剑剑的代码:

- 小剑剑的代码中把输入和判断放在一起,这样子可以避免特意多出一个循环去判断是不是上三角的情况,会高效很多。
2.2 找鞍点
2.2.1 伪代码
用状态变量flag = 1来区分是否找到鞍点的情况。当下表示有鞍点
scanf输入n
for from j = 0 to n
for from i = 0 to n
scanf array[j][i]
for from i = 0 to n
flag = 1 每一次从新的一行开始,状态变量都应该更新为默认有鞍点存在的状态。
col = i;
for from j = 1 to n
比较array[i][col] <= array[i][j] 查找看是否同一行最大的那个元素的列下标,
由此找到行最大 col = j; 加等号是为了保证极值并列的情况下,取后一个数为鞍点。
for from x = 0 to n
比较array[i][col] > array[x][col] 查找行最大的这个下标对应的元素在其所在的列是否为最小,
如果不是的话 flag = 0;
在循环最后同过flag的值来判断这一轮寻找是否有找到鞍点,如果有的话,row = i 并 结束循环
循环外进行统一输出,以状态变量为条件分别控制有无鞍点情况的输出。
2.2.2 代码如下:
//找鞍点
#include<stdio.h>
int main()
{
//数据表达
int n;
int i, j, x;
int array[6][6];
int col, row;
int flag = 1;//用来表示是否存在鞍点;
//流程设计
//input:
scanf("%d", &n);
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
scanf("%d", &array[i][j]);
}
}
//judgement:
for (i = 0; i < n; i++)
{
flag = 1;//每一行开始的起始都应该怀着可能找到鞍点的状态;
col = 0;
//找到本行最大的那个数的列下标;
for (j = 1; j < n; j++)
{
if (array[i][col] <= array[i][j])
//加上等号是如果遇到一样大的,取后面的,不取前面的。
{
col = j;
}
}
//拿这行下下标最大的数和它所在列的其他数进行对比;
for (x = 0; x < n; x++)
{
if (array[i][col] > array[x][col] && x != i)
{
flag = 0;/*如果在该列中存在比这个行最大的数小的数,
那就说明,这个行最大的数不是鞍点。*/
break;//这是分析老师的代码之后加上去提高效率的。
}
}
//即时跳出有鞍点的情况
if (flag == 1)
{
row = i;
break;
}
}
if (flag)
{
printf("%d %d", row, col);
}
else
{
printf("NONE");
}
return 0;
}
2.2.3 请说明和超星视频做法区别,各自优缺点。
- 其实主体思路大概都是一样的。都是先找到某一行中的最大元素,然后在对这一行中最大元素所在的列进行遍历,
比较得出是否可能存在该元素在所在列最小,有鞍点的情况。 - 不同的是,我对是否找到鞍点是采用状态变量进行标识,这里要注意到的一个小细节是,每一次从新的一行开始
寻找都意味着有可能存在鞍点的情况,但是上一行的查找中不存在鞍点的判定结果中,是把flag的状态变成0了,所
以要记得使用状态变量来为分类情况的时候,要记得时刻关注在进程中,状态变量是否在对应时刻一直保持着它所
应该保持的状态所对应的值关键点在于重视状态变量的每一个需要变化的点。
本题的细节主要在于,每一次从新的一行开始寻找都意味着有可能存在鞍点的情况所以应该在外循环开头加上
flag = 1来保证这一点。 - 而老师的做法用来控制数据是否合理的情况却是,直接让不满足情况的条件跳出循环,这样的情况下,便可以用循环
控制变量和n进行比较来确认是否存在鞍点,如果能走完循环即循环控制及变量等于n则表示能找到鞍点,否则中途跳出
的情况则表示没有找到鞍点。这样的话,对于没有找到鞍点的情况能直接跳出减少不必要的循环次数,提高运行效率。 - 对我的代码的改进就是在flag = 0后面加上一条break语句。
2.2.4 或许这道题目可能存在测试数据的不够丰富:
俺在深度思考的过程中造了这组数据对能过pta的我的代码
进行了测试最后发现得出的结果和实际情况不太吻合。
这组测试数据为:
我造的有鞍点的特殊数据
(行上有并列极值,存在鞍点,但鞍点不为后,而应该在前一个)
4
1 7 4 8
4 8 3 5
1 6 1 6
0 7 8 9
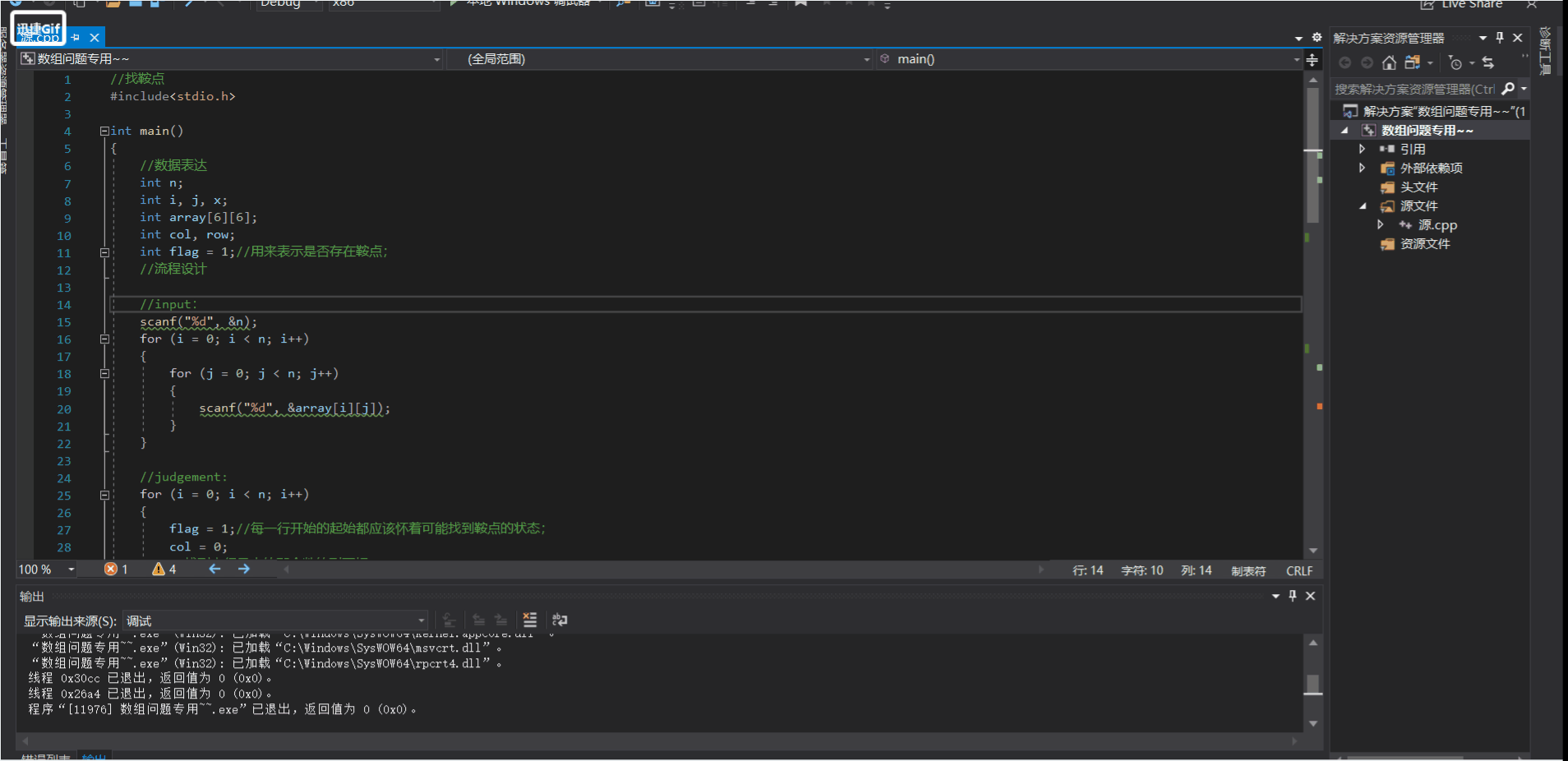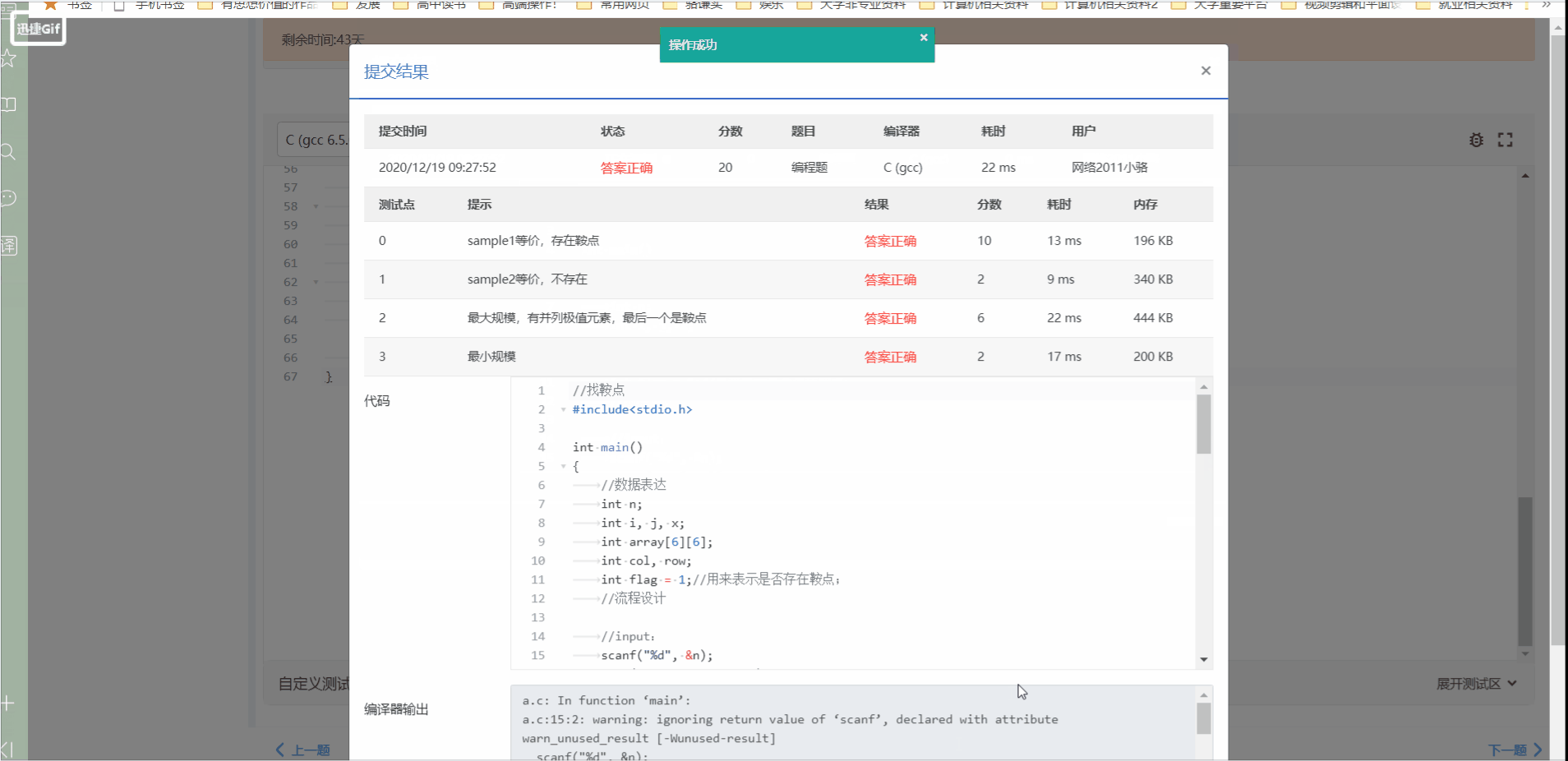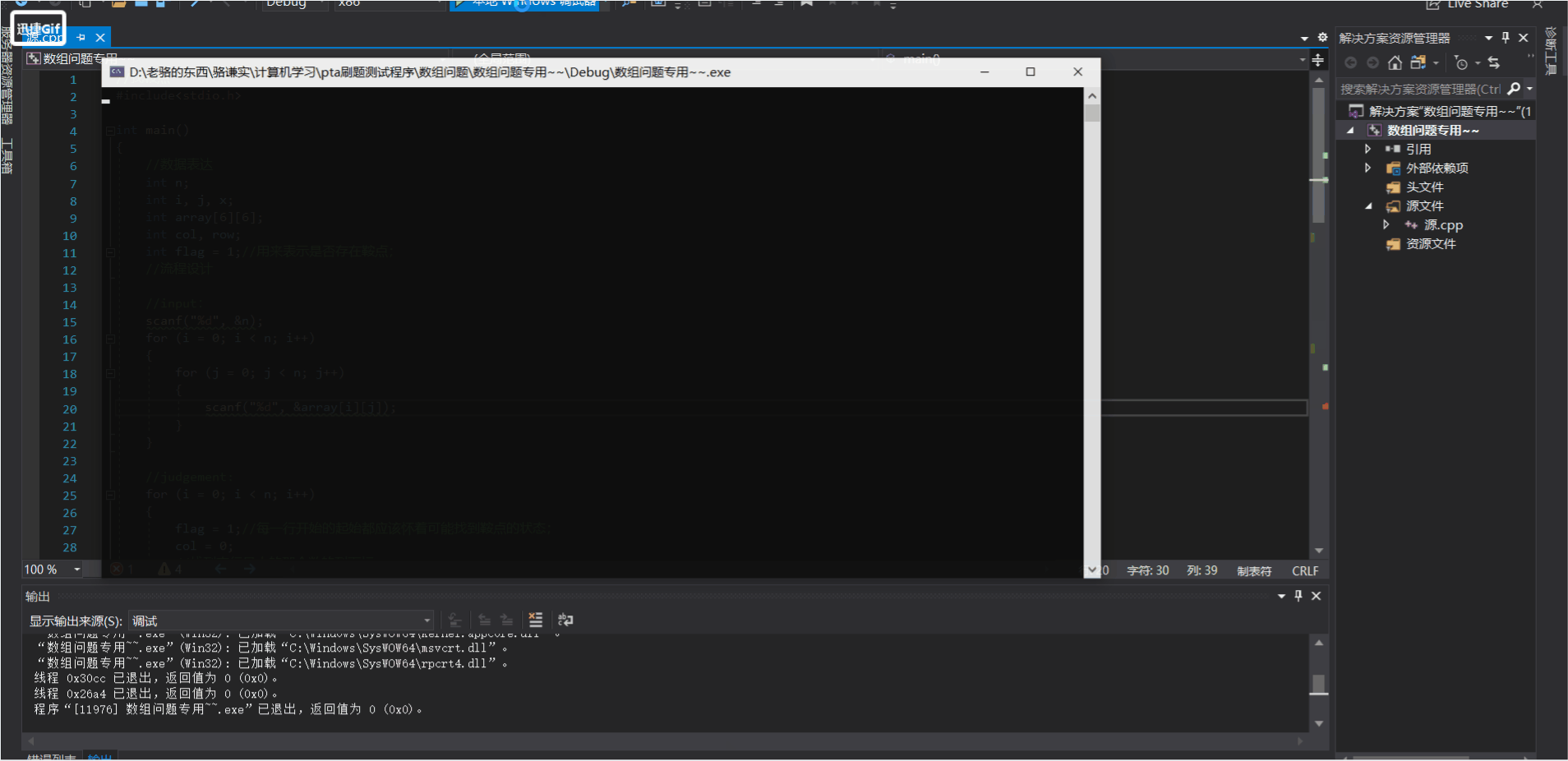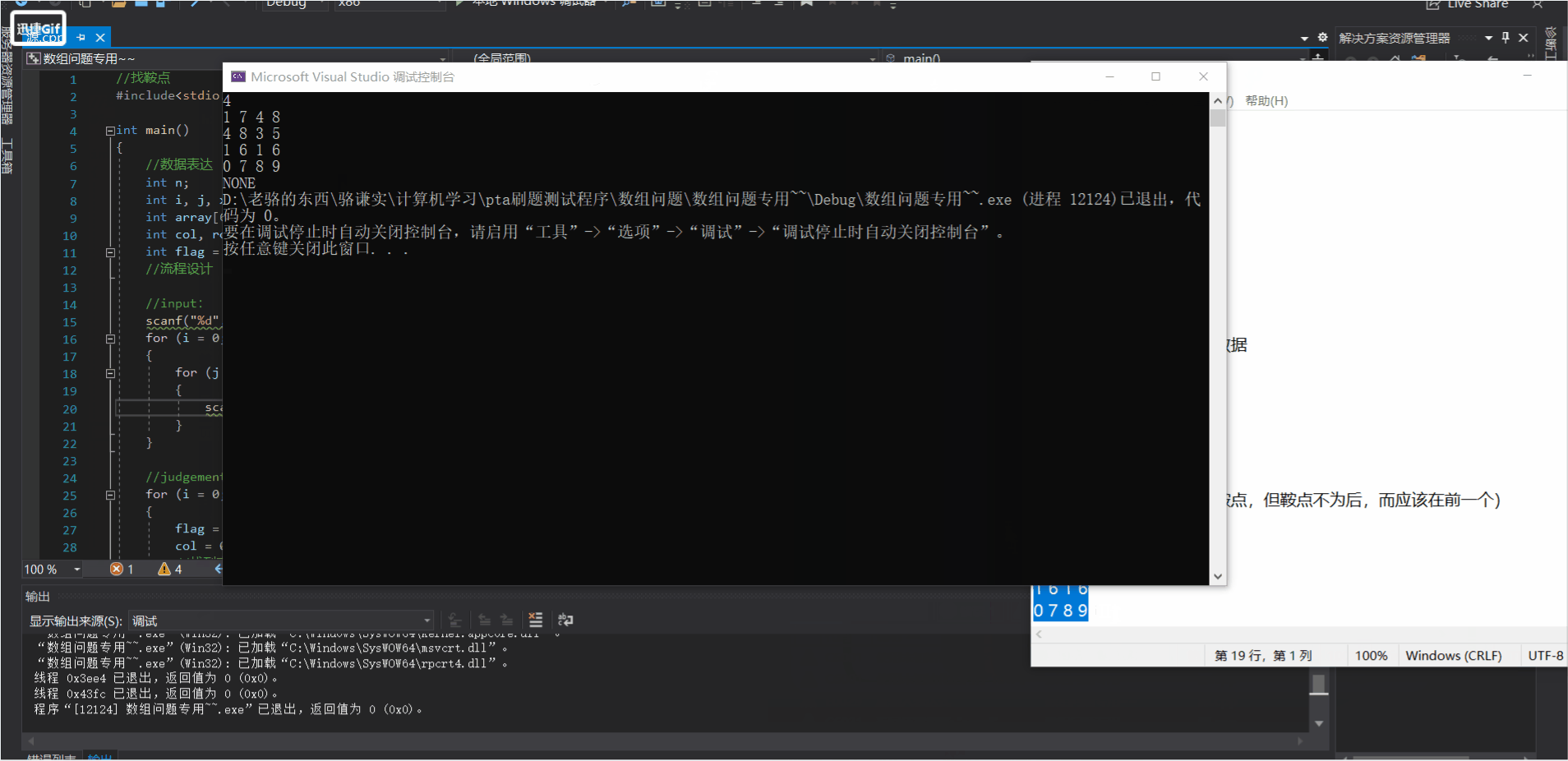
按道理说 这里是存在鞍点的且应该为输出为 2 1,但结果是并没有。所以我大胆地认为。
PTA可能存在测试数据的缺少乃至老师和俺的目前给出的代码都有调试的空间!
对提出问题的解决,先等俺肝完作业趴~~~(狗头保命)
2.3 切分表达式(2分)
2.3.1 伪代码
用scanf进行输入这一串表达式
然后首先对数字进行判定,
if 输入的是数字的话进行如下判定
if下一个字符是结束字符'\0'的话,那也不换行
else if下一个字符是其他字符 且 这个字符不是小数点的话就直接换行
else 下一个字符是数字或者小数点都不换行。
else if是对比较特殊的减号进行判定
if减号在开头的话,那就不换行
else if如果减号前面的字符不是数字 且 i = 0的话,那就不换行
else 这时候充当的是减号那就换行。
else if是对加号这个特殊的符号进行判断
if i == 0,输出不换行
else 输出换行充当加号。
else if 其他的字符
if 下一个字符是结束字符的话那就不换行
else 其他全部统统换行输出。
2.3.2 代码截图
- 原始的版本:
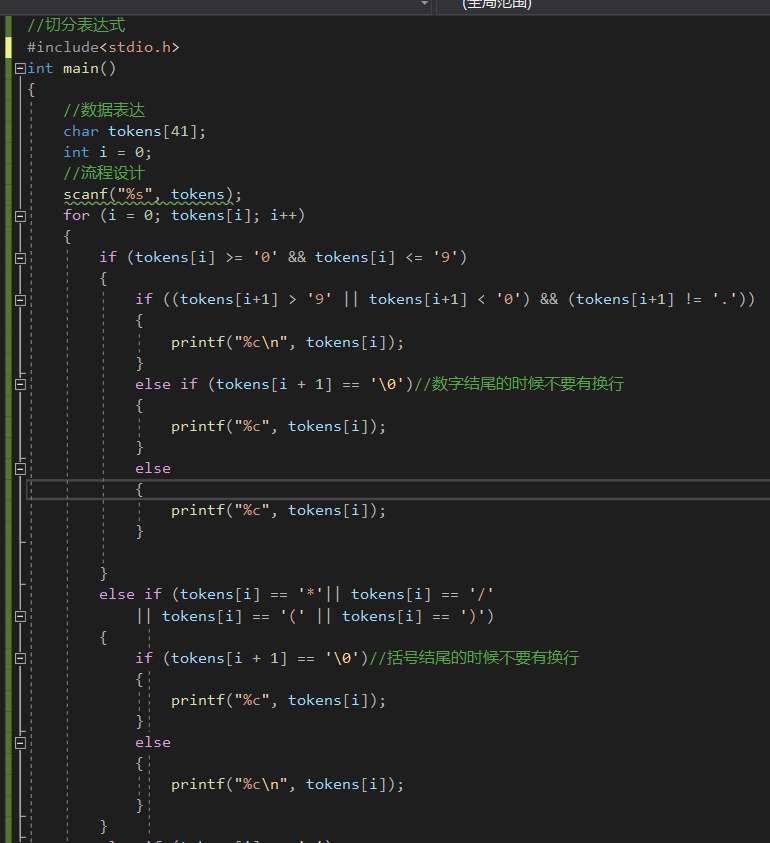
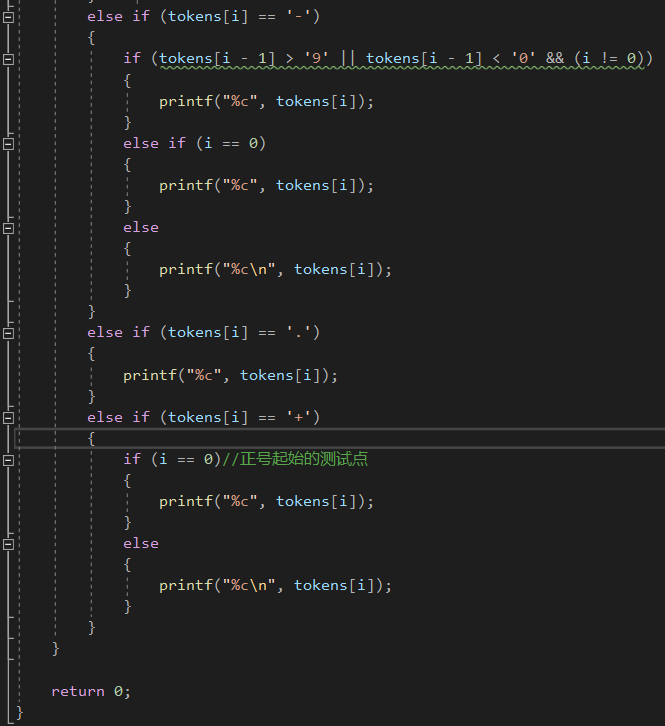
*看完超星视频后的改动版:
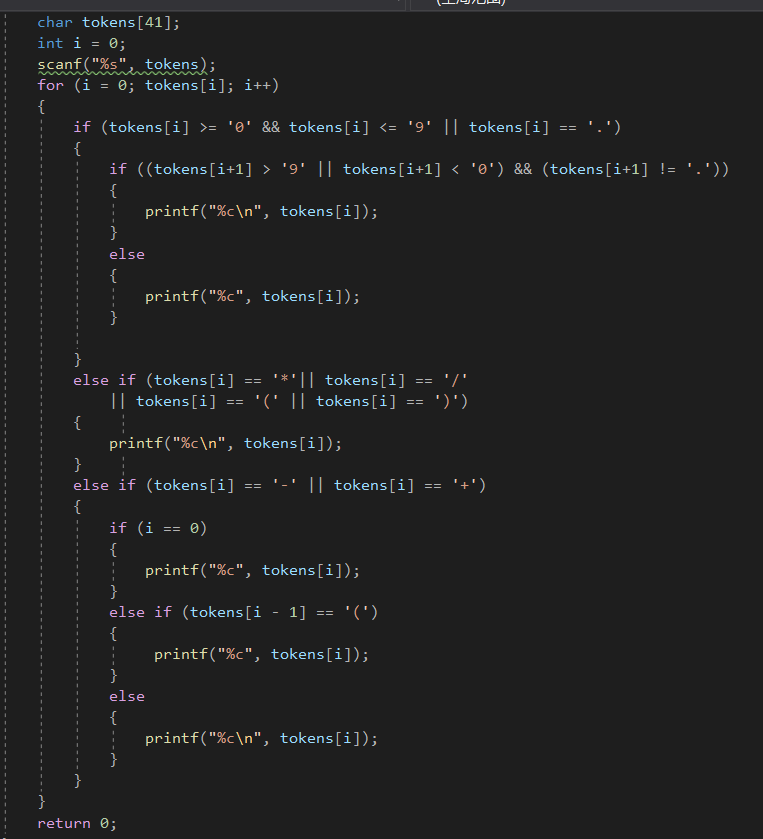
2.3.3 请说明和超星视频做法区别,各自优缺点。
- 主要的区别是在于,对于提高代码效率的判断上面,老师使用的是i++和continue语句,而我是直接用级联的分支结构
来构成整个表达体。但达到的效果是差不多的。 - 另外要向老师学习的地方是,老师在做题前的分析上会比我强很多,这道题我的思路是先把sample的效果做出来,
然后再去根据测试点一个一个改动,体现在结构上的问题就是不够彻底。伪代码的分析上就可以看出来了。比如其实
正负号是可以归到一起去同时处理的。并且判断在表达式中间充当正负号的情况用前一个是'('会比前一个不是数字
的条件来得精确。 - 小细节要注意,else-if中,能到else-if隐含了上一级条件不满足的情况。按这个思路去写和排序可以简化代码。
- 以及他并没有要求结尾不需要换行,我画蛇添足了!

