DS博客作业04--图
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业04--图 |
| 这个作业的目标 | 学习图结构设计及相关算法 |
| 姓名 | 骆念念 |
0.PTA得分截图
图题目集总得分，请截图，截图中必须有自己名字。题目至少完成2/3，否则本次作业最高分5分。
1.本周学习总结（6分）
本次所有总结内容，请务必自己造一个图（不在教材或PPT出现的图），围绕这个图展开分析。建议：Python画图展示。图的结构尽量复杂，以便后续可以做最短路径、最小生成树的分析。
1.1 图的存储结构
1.1.1 邻接矩阵（不用PPT上的图）
实现图的最简单的方法之一是使用二维矩阵。在该矩阵实现中，每个行和列表示图中的顶点。存储在行 v 和列 w 的交叉点处的单元中的值表示是否存在从顶点 v 到顶点 w 的边。当两个顶点通过边连接时，它们是相邻的。单元格中的值表示从顶点 v 到顶点 w 的边的权重。一个图的邻接矩阵不是唯一的，在无向图中，邻接矩阵为对称矩阵。邻接矩阵适合用于存储稠密图。
如何在邻接矩阵中找入度出度
在一个无向图中，一个的顶点行或列就是它的入度/出度
在有向图中，一个顶点的行是出度，它的列就是入度，两个相加就是边
造一个图，展示其对应邻接矩阵
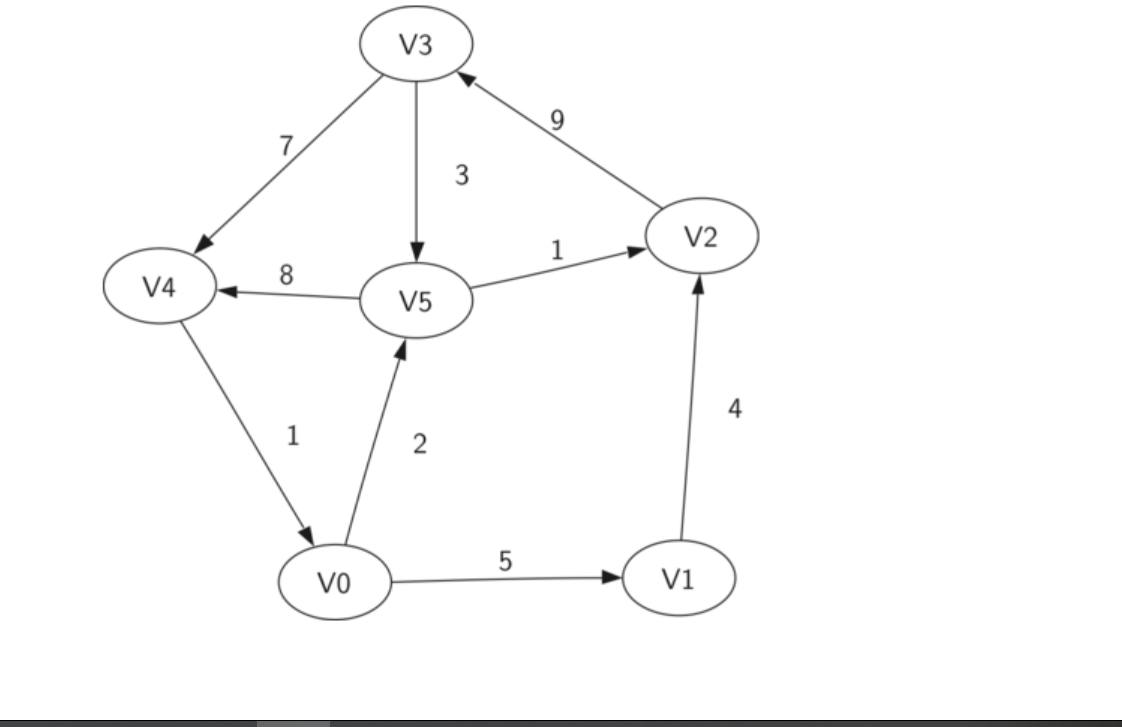
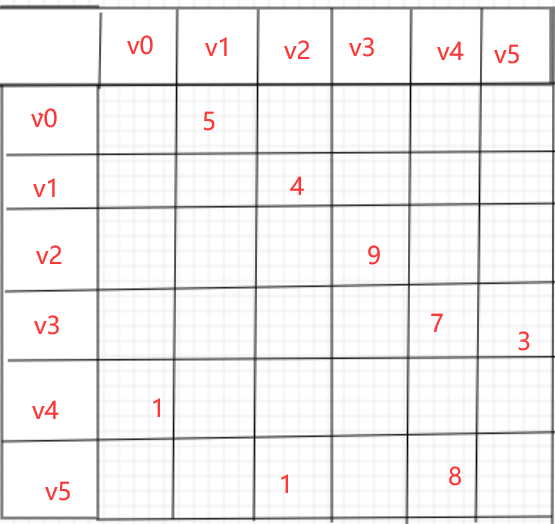
邻接矩阵的结构体定义
typedef struct
{
int no;//顶点编号
InfoType info;//顶点其他信息
}VertexType;
typedef struct
{
int edges[MAXV][MAXV];
int n,e;
VertexType vexs[MAXV];
}MatGraph;
建图函数
void CreatMGraph(MGraph &g,int n,int e)
{
int i,j,a,b;
//初始化矩阵
for(i=0;i<n;i++)
for(j=0;j<n;j++)
g.edgs[i][j]=0;
for(i=1;i<=e;i++)
{
g.edges[a-1][b-1]=1;
g.edges[b-1][a-1]=1;
}
g.n=n;
g.e=e;
}
1.1.2 邻接表
邻接表，存储方法跟树的孩子链表示法相类似，是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点，则把相邻顶点依次存放于表头结点所指向的单向链表中。对于无向图来说，使用邻接表进行存储也会出现数据冗余，表头结点A所指链表中存在一个指向C的表结点的同时，表头结点C所指链表也会存在一个指向A的表结点。
造一个图，展示其对应邻接表（不用PPT上的图）
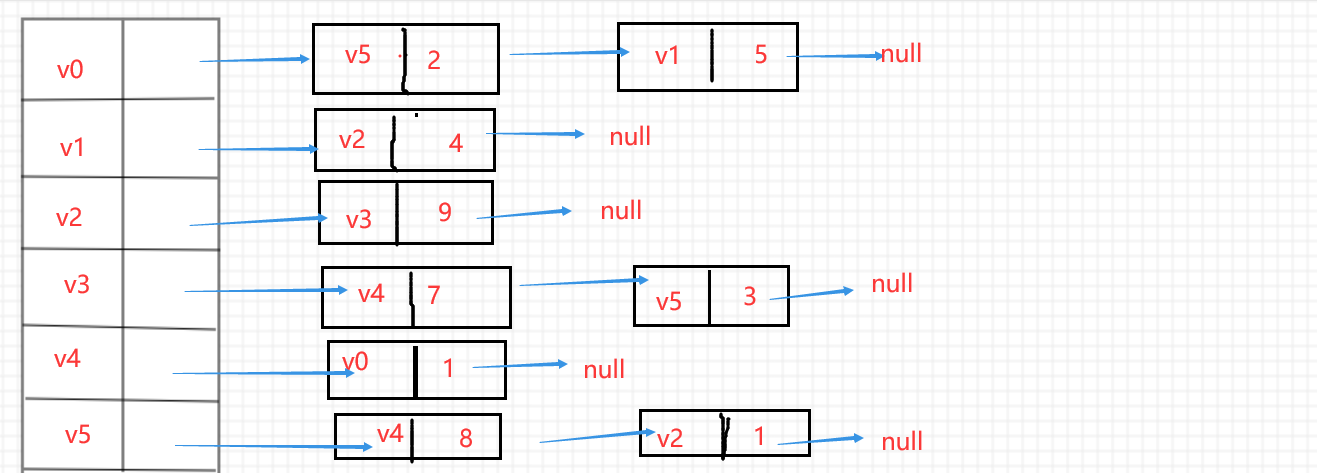
邻接矩阵的结构体定义
typedef struct ANode
{
int adjvex;//边
struct ANode *nextarc;指向下一条边
InfoType info;
}ArcNode;
typedef struct Vnode
{
Vertex data;
ArcNode *firstarc;
}VNode;
typedef struct
{
VNode adjlist[MAXV];
int n,e;
}AdjGraph;
建图函数
void CreateAdj(AdjGraph *&G,int n,int e)
{
int i,j,a,b;
ArcNode *p;
G=new AdjGraph;
for(i=0;i<n;i++)
G->adjlist[i].firstarc=NULL;
for(i=1;i<=e;i++)
{
cin>>a>>b;
p=new ArcNode;
p->adjvex=b;
p->nextarc=G->adjlist[a].firstarc;
G->adjlist[a].firstarc=p;
//无向图时
p=new ArcNode;
p->adjvex=a;
p->nextarc=G->adjlist[b].firstarc;
G->adjlist[b].firstarc=p;
}
G->n=n;
G->e=e;
1.1.3 邻接矩阵和邻接表表示图的区别
各个结构适用什么图？时间复杂度的区别。
邻接矩阵适合稠密图，邻接表适合稀疏图。邻接矩阵的时间复杂度是O（n*n），邻接表的时间复杂度是O（n+e）。
1.2 图遍历
1.2.1 深度优先遍历
选上述的图，继续介绍深度优先遍历结果
主要思路是从图中一个未访问的顶点 V 开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底...，不断递归重复此过程，直到所有的顶点都遍历完成，它的特点是不撞南墙不回头，先走完一条路，再换一条路继续走。
上图的深度优先搜索为：v1,v2,v3,v5,v4,v6
深度遍历代码
//邻接表
vois DFS(ALGraph *G,int v)
{
ArcNode *p;
visited[v]=1;
cout<<v;
p=G->adjlist[v].firstarc;
while(p!=NULL)
{
if(visited[p->adjvex]==0)
DFS(G,p->adjvex);
p=p->nextarc;
}
}
邻接矩阵
void DFS(MGraph g, int v)//深度遍历
{
int i;
visited[v] = 1;
if (flag==1)
cout << " " << v;
else
{
cout << v;
flag = 1;
}
for (i = 1; i <= g.n; i++)
if (g.edges[v][i] == 1 && visited[i]==0)
DFS(g, i);
}
深度遍历适用哪些问题的求解。（可百度搜索）
可以用来拓扑排序，寻路(走迷宫)，搜索引擎，爬虫等。
1.2.2 广度优先遍历
选上述的图，继续介绍广度优先遍历结果
广度优先遍历，指的是从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点。
上图的广度遍历为：v1,v2,v3,v5,v4,v6
广度遍历代码
//邻接表
void BFS(ALGraph *G,int v)
{
queue<int>q;
int w;
ArcNode *p;
for(i=0;i<g.n;i++)
{
q.push(v);
visited[v]=1;
cout<<v;
while(!q.empty())
{
w=q.front();
q.pop();
p=G.adjlist[w].firstarc;
while(p!=NULL)
{
w=p->adjvex;
if(visited[w]==0)
{
q.push(w);
visited[w]=1;
cout<<w;
}
p=p->nextarc;
}
}
}
//邻接矩阵
void BFS(MGraph g, int v)//广度遍历
{
int t;
queue<int>q;
if (visited[v] == 0)
{
cout << v;
visited[v] = 1;
q.push(v);
}
while (!q.empty())
{
t = q.front();
q.pop();
for (int j = 1; j <= g.n; j++)
{
if (g.edges[t][j] == 1 && visited[j] == 0)
{
cout << " " << j;
visited[j] = 1;
q.push(j);
}
}
}
}
广度遍历适用哪些问题的求解。（可百度搜索）
广度优先搜索可用于在像对等网络中找到邻居节点，如BitTorrent，用于查找附近位置的GPS系统，用于查找指定距离内的人的社交网站以及类似的东西。
1.3 最小生成树
用自己语言描述什么是最小生成树。
最小生成树，首先最小就说明了权值最小，树就说明不能构成回路。最小生成树就是由n-1条边组成的并且权值最小的树。
1.3.1 Prim算法求最小生成树
基于上述图结构求Prim算法生成的最小生成树的边序列
其最小生成树序列为：
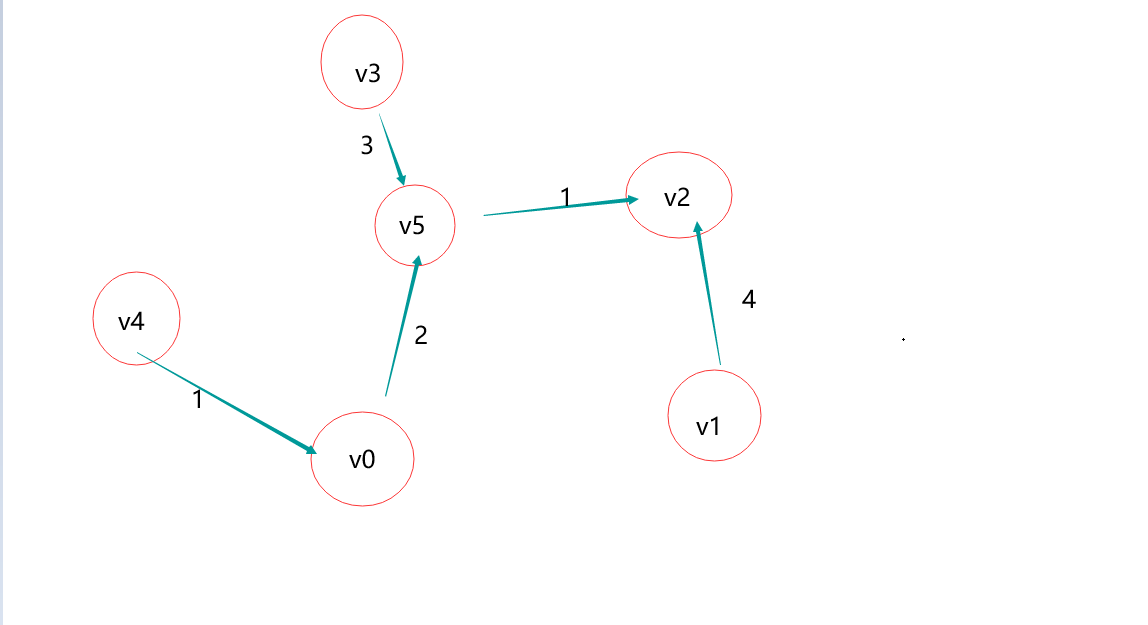
实现Prim算法的2个辅助数组是什么？其作用是什么？Prim算法代码。
两个辅助数组为closest[],lowcost[]。lowcost[]是侯选边数组，其值为候选顶点到U中的最小边。closest[]依附在U中顶点。
void Prim(MGraph g,int v)
{
int lowcost[MAXV],min,closest[MAXV],i,j,k;
for(i=0;i<g.n;i++)
{
lowcost[i]=g.edges[v][i];
closest[i]=v;
}
for(i=1;i<g.n;i++)
{
min=INF;
for(j=0;j<g.n;j++)
if(lowcost[j]!=0&&lowcost[j]<min)
{
min=lowcost[j];
k=j;
cout<<closest[k]<<k<<min;
lowcost[k]=0;
for(j=0;j<g.n;j++)
if(g.edges[k][j]!=0&&g.edges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j];
closest[j]=k;
}
}
}
分析Prim算法时间复杂度，适用什么图结构，为什么？
时间复杂度为O（n^2）。适合用于图的邻接矩阵。
1.3.2 Kruskal算法求解最小生成树
基于上述图结构求Kruskal算法生成的最小生成树的边序列
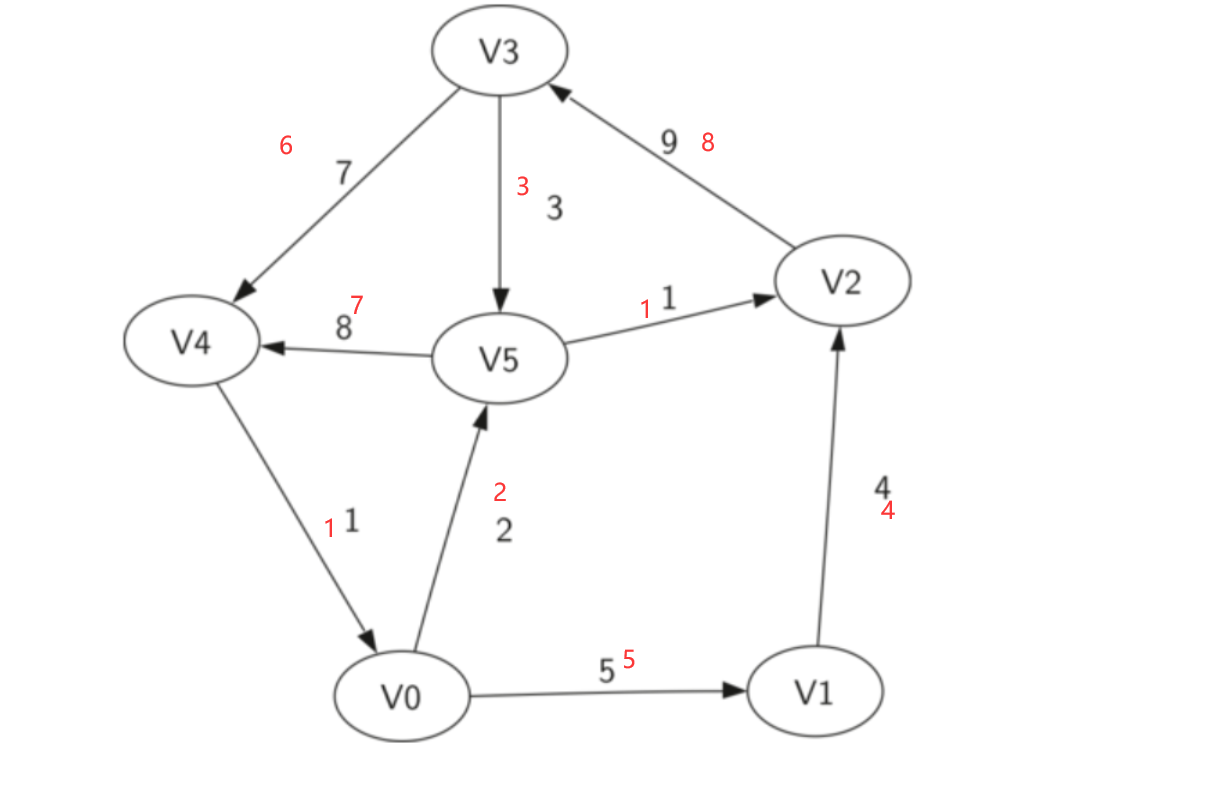
实现Kruskal算法的辅助数据结构是什么？其作用是什么？Kruskal算法代码。
vset[MAXV]集合辅助数组，Edge E[MaxSize]存放所有边
void Kruskal(AdjGraph *g)
{
int i,j,u1,v1,sn1,sn2,k;
int vset[MAXV];
Edge E[MaxSize];
for(i=0;i<.n;i++)
{
p=g->adjlist[i].firstarc;
while(p!=NULL)
{
E[k[.u=i;
E[k].v=p->adjvex;
E[k].w=p->weight;
k++;
p=p->nextarc;
}
InserSort(E,g.e）；
for(i=0;i<g.n;i++)
vset[i]=i;
k=1;
j=0;
while(k<g.n)
{
u1=E[j].u;
v1=E[j].v;
sn1=vset[u1];
sn2=vset[v1];
if(sn1!=sn2)
{
cout<<u1<<v1<<E[j].w;
k++;
for(i=0;i<g.n;i++)
if(vset[i]==sn2)
vset[i]=sn1;
}
j++;
}
}
分析Kruskal算法时间复杂度，适用什么图结构，为什么？
适用于邻接表，时间复杂度O（n）。
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
基于上述图结构，求解某个顶点到其他顶点最短路径。（结合dist数组、path数组求解）
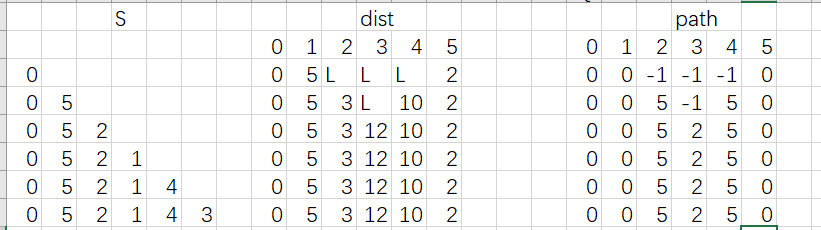
Dijkstra算法需要哪些辅助数据结构
需要dist[],path[]数组。
Dijkstra算法如何解决贪心算法无法求最优解问题？展示算法中解决的代码。
void Dijkstra(MatGraph g,int v)
{
int dist[MAXV],path[MAXV];
int s[MAXV];
int mindis,i,j,u;
for(i=0;i<g.n;i++)
{
dist[i]]g.edges[v][i];
s[i]=0;
if(g.edges[v][i]<INF)
path[i]=v;
else
path[i]=-1;
}
s[v]=1;
for(i=0;i<g.n;i++)
{
midsit=INF;
for(j=0;j<g.n;j++)
if(s[j]==0&&dist[j]<mindis)
{
u=j;
mindis=dist[j];
}
s[u]=1;
for(j=0;j<g.n;j++)
if(s[j]==0)
if(g.edges[u][j]<INF&&dist[u]+g.edges[u][j]<dist[j])
{
dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
Dispath(dist,s,g,v);
}
Dijkstra算法的时间复杂度，使用什么图结构，为什么。
O(nn);使用邻接矩阵。每次比较最小时，都是用dist和该最小边与其它边的和比较，用邻接矩阵方便。*
1.4.2 Floyd算法求解最短路径
Floyd算法解决什么问题？
用来求所有点之间的最短路径。
Floyd算法需要哪些辅助数据结构
需要A[][]数组和path[][]数组。
Floyd算法优势，举例说明。
优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。
缺点：时间复杂度比较高，不适合计算大量数据
最短路径算法还有其他算法，可以自行百度搜索，并和教材算法比较。
Bellman-Ford 算法
遵循一个比一个强大的规则，这个算法可以处理负权重的环，只不过存在负权重环的话，就可能没有最短路径存在了，无限转圈…
Floyd算法和Dijkstra算法的思考角度差不多，都是从顶点的角度出发去松弛边，前者比后者充满了暴力般的简洁。而Bellman-Ford 并不是纯粹从顶点出发的思路，而是外层循环顶点，内层循环边，和Dijkstra相似的是，也是处理从单个顶点出发求到其它所有顶点的最短距离，具体思路如下：
1.首先，定义一个dis数组，表示原点到其它结点的距离，初始化为无穷大，
先考虑一轮循环，加入第一条边w(u,v)，很明显，除非u或者v中有一个是原点，才能更新dis数组
2.再加入一条边，考虑一种特殊情况，第一次加入的u是原点，这样，更新了原点到v的距离，这次的加入是w(v,v2)，那么很明显，v2也能更新了，需要w(u,v)+w(v,v2)，但是能直接更新吗？先需要和当前值比以下，取较小值才是合理的，当然只有两条边的情况下是和无穷在比较
3.再加入第三条边，加入碰巧是w(u,v2)，显然需要和第二步的值做比较才能决定更新
不断的加入新的边w(x,y)，统一的计算dis[x] + w(x,y) < dis[y]吗？小于则更新dis[y]
4.全部的边都加入了，是不是求出了原点到其它结点的最短距离呢？有可能。分析第一轮循环做了哪些，加入一条边w(x,y)，就算一下从原点到y的距离是不是先经过x再到y会更短，但是值得注意，上面的特殊情况是先加入和原点相邻的边，再加入和原点相邻的边的相邻的边，如果相反呢，那么判断原点到相邻的边距离是无穷大，明显就不会更新了，也就没有路径中存在两个边的情况了。
5.所以需要再更新，之前的更新dis假设保留了只经过一条边结果，这一轮更新，便能把经过2条边的情况包含进去，因为每轮更新都只能再上一轮更新的基础上再加一条边
所以考虑极端情况，最短路径包含n-1条边，那么就需要n-1轮更新
6.另外，如果某一轮更新后，dis值没有变化，那么更新就可以停止，如果n-1轮更新完毕后dis还有变化，说明存在负环
7.复杂度的话明显是顶点个数边的个数*
1.5 拓扑排序
找一个有向图，并求其对要的拓扑排序序列
拓扑排序的方法：
1.从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出。
2.从图中删除该顶点和所有以它为起点的有向边。
3.重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。
它的拓扑排序为：1,2,4,3,5
实现拓扑排序代码，结构体如何设计？
typedef struct//表头节点类型
{
vertex data;顶点信息
int count;存放顶点入度
ArcNode *firstarc;指向第一条弧
}VNode;
书写拓扑排序伪代码，介绍拓扑排序如何删除入度为0的结点？
遍历邻接表
计算每个顶点的入度，存入头结点count成员
遍历图顶点
若发现入度为0的顶点，入栈st
while(栈不空)
{
出栈节点v，访问
遍历v的所有邻接点
{
所有邻接点的入度为-1
若有邻接点入度为0，则入栈st
}
}
如何用拓扑排序代码检查一个有向图是否有环路？
#include <iostream>
#include <queue>
#include <string>
using namespace std;
//表结点
typedef struct ArcNode{
int adjvex;//该弧所指向的顶点的位置
ArcNode *nextarc;
}ArcNode;
//头结点
typedef struct VNode{
string data;//顶点信息
ArcNode *firstarc;//第一个表结点的地址，指向第一条依附该顶点的弧的指针
}VNode, AdjList[10];
typedef struct ALGraph{
AdjList vertices;
int vexnum, arcnum;
}ALGraph;
int LocateVex(ALGraph G, string u)//返回顶点u在图中的位置
{
for(int i=0; i<G.vexnum; i++)
if(G.vertices[i].data==u)
return i;
return -1;
}
void CreateDG(ALGraph &G)//构造有向图
{
string v1, v2;
int i, j, k;
cout<<"请输入顶点数和边数：";
cin>>G.vexnum>>G.arcnum;
cout<<"请输入顶点：";
for(i=0; i<G.vexnum; i++)
{
cin>>G.vertices[i].data;
G.vertices[i].firstarc=NULL;
}
cout<<"请输入边："<<endl;
for(k=0; k<G.arcnum; k++)
{
cin>>v1>>v2;
i=LocateVex(G, v1);
j=LocateVex(G, v2);
ArcNode* arc=new ArcNode;
arc->adjvex=j;
arc->nextarc=G.vertices[i].firstarc;
G.vertices[i].firstarc=arc;
}
}
void FindIndegree(ALGraph G, int indegree[])//求顶点的入度
{
for(int i=0; i<G.vexnum; i++)
indegree[i]=0;
for(i=0; i<G.vexnum; i++)
{
ArcNode *p=G.vertices[i].firstarc;
while(p)
{
indegree[p->adjvex]++;
p=p->nextarc;
}
}
}
void TopologicalSort(ALGraph G)//拓扑排序
{
queue<int> q;
int indegree[10]={0};//入度数组
int count=0;//计数，计入队数
FindIndegree(G, indegree);
for(int i=0; i<G.vexnum; i++)//入度为0的顶点入队
if(0==indegree[i])
q.push(i);
while(!q.empty())
{
int v=q.front();
q.pop();
count++;
cout<<G.vertices[v].data<<" ";
ArcNode *p=G.vertices[v].firstarc;
while(p)//出队后，每个邻接点入度减1
{
if(!(--indegree[p->adjvex]))
q.push(p->adjvex);//入度为0的顶点入队
p=p->nextarc;
}
}
if(count<G.vexnum)//由此判断有向图是否有回路
cout<<"该有向图有回路"<<endl;
}
void main()
{
ALGraph G;
CreateDG(G);
cout<<"拓扑排序：";
TopologicalSort(G);
cout<<endl;
}
1.6 关键路径
什么叫AOE-网？
用顶点表示事件，用有向边e表示活动，边的权表示活动持续的时间，是带权的有向无环图。
什么是关键路径概念？
整个工程完成的时间为：从有向图的源点到汇点的最长路径，又叫关键路径。
什么是关键活动？
关键活动指的是关键路径中的边
2.PTA实验作业（4分）
2.1 六度空间（2分）
选一题，介绍伪代码，不要贴代码。请结合图形展开分析思路。
2.1.1 伪代码（贴代码，本题0分）
伪代码为思路总结，不是简单翻译代码。
先定义i作为循环变量，定义vis数组作为所有节点的存放数组
定义level作为开关变量count作为，定义栈q
主函数中定义v作为节点总数，e作为邻接矩阵层数
while循环给数组赋值，也就相当于给邻接矩阵赋值
for 1 to v循环执行bfs函数和题目要求 输出所需的数据
bfs函数中定义上面，首先while给定的条件是栈不为空时进行遍历
count用于记录距离不超过6的节点的个数
if则是判断是否遍历完一层，跳入下一层的操作
这个地方需要不断更新每一层的最后一个结点的位置lats
当level=6也就是最大距离的时候跳出循环把这个数返回
2.1.2 提交列表
2.1.3 本题知识点
本题用到了栈，广度遍历和层次遍历的知识点
2.2 村村通或通信网络设计或旅游规划（2分）
旅游规划
2.2.1 伪代码（贴代码，本题0分）
伪代码为思路总结，不是简单翻译代码。
这道题的思路就是计算两个结点之间的最短路径和计算最短路径上的权值
首先定义的邻接矩阵的数组和顶点数弧数
int know[maxv],know[]=1表示求得最短路径
int distance[maxv]表示求的最短距离
int pay[maxv]表示最少费用
首先是主函数中，输入题目的信息后执行建图和找路径函数
if判断是否最短路径符合要求 符合要求在进行输出
使用邻接矩阵图结构
用Dijkstra找路径函数
定义ij循环变量
k作为记录节点位置的变量
定义min作为最短路径上节点的编号 cost作为每条边上的权
for i=0 to nv循环里执行的操作是把每个与v有联系的节点机上权
接下来初始化三个数组
for i=0 to nv的循环操作是找出最短路径
for j=0 to nv的循环操作是重复找出离当前节点最近的节点并且记录名称和对应的权值
再次初始化 利用prim算法对路径进行修正
2.2.2 提交列表
2.2.3 本题知识点
利用用Dijkstra找路径函数，邻接矩阵建图
