第三次实验报告
C程序设计实验报告
实验项目:
1、用for语句实现循环
2、用while循环语句实现循环
3、用do-while语句实现循环
4、用while语句和for语句配合实现循环
5、用for语句嵌套实现循环
姓名:罗龙妹 实验地点: 514实验室 实验时间:2019年4月17日
一、实验目的与要求
1、用for语句实现循环
- 掌握for语句实现循环的方法
- 循环嵌套的使用
2、用while循环语句实现循环 - 掌握while语句实现循环的方法
- 进一步掌握while语句实现循环的方法
3、用do-while语句实现循环 - 掌握do/while语句实现循环
4、用while语句和for语句配合实现循环。 - 掌握while语句和for语句配合实现循环
5、用for语句嵌套实现循环 - 掌握for语句嵌套实现循环的方法
- 掌握for语句嵌套(3层)实现循环的方法
- 掌握continue语句的用法
二、实验内容
5.3.1:用for语句实现循环
实验练习1:求数列前n项
- 问题的简单描述:编写一程序,求出1,1+2,1+2+3···数列中前n项的值。
- 程序流程图:
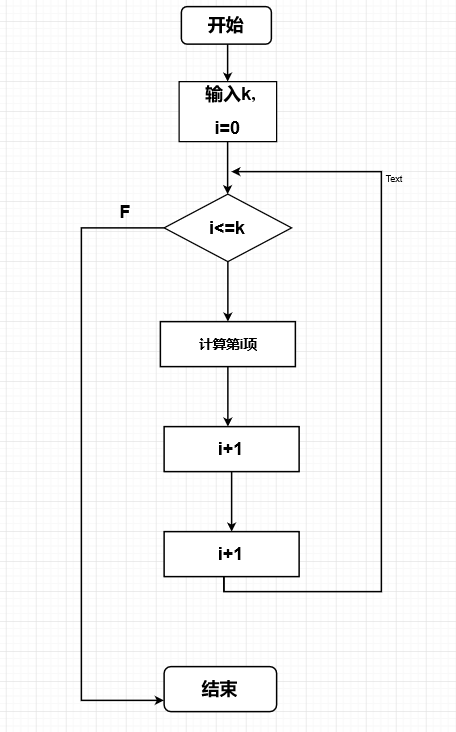
- 实验代码:
#include<stdio.h>
#include<conio.h>
main()
{
int i,j=0,k,s=0;
printf("Enter a number:");
scanf("%d",&k);
for(i=1;i<=k;i++)
{
s=s+i;
printf("%d\t",s);
j++;
}
}
- 问题分析:(重点分析在实验过程中出现的问题,及解决方法。)
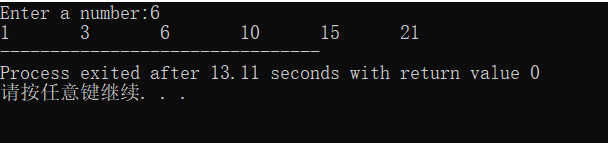
这道题是要求数列1,1+2,1+2+3···前n项的和,程序代码中s代表前n项的和,i代表第i项的数,i从1开始每次加1开始累加,s则是根据s+i累加。 - 程序运行如下:
实验练习2:求数列前n项的和 - 问题的简单描述:编写一程序,求数列1,-3!,5!,-7!···[(-1)^(n-1)]*(2n-1)!前n项的和。n的值由键盘输入。
- 程序流程图:
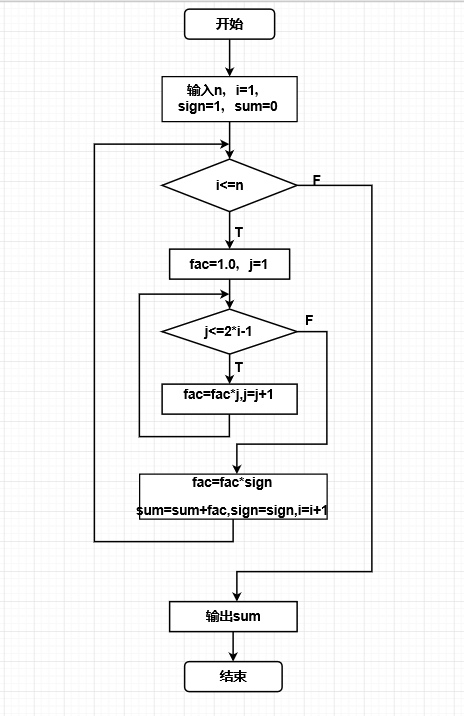
- 实验代码:
#include<stdio.h>
main()
{
int n,i,j,sign=1;
float fac,sum;
printf("please input value of n:");
scanf("%d",&n);
sum=0.0;
for(i=1;i<=n;i=i+1)
{
fac=1.0;
for(j=1;j<=2*i-1;j++)
{
fac=fac*j;
}
fac=fac*sign;
sum=sum+fac;
sign=-sign;
}
printf("sum=%.0f\n",sum);
}
- 问题分析:
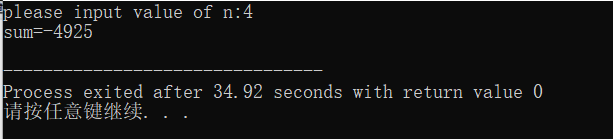
这道题是要求数列1,-3!,5!,-7!···[(-1)^(n-1)]*(2n-1)!前n项的和,需要用到两个for循环,第一个for循环使控制项数,第二个for循环即求数列的前n项和。书本中给出的第一个for循环的条件表达式是错误的,如果按照书本中的来那便永远也得不出正确的答案,不过要我自己发现的话可能有点难,还是老师在我们做之前就提醒我们了,我才知道,而且我干开始做的时候也没有用两个for循环,导致一直出不来正确的答案,最后还是旁边同学提醒了我。 - 程序运行如下:
5.3.2:用while循环语句实现循环
实验练习1:统计学生的最高最低成绩
- 问题的简单描述:从键盘上输入若干学生的成绩,统计并输入最高成绩和最低成绩,当输入负数时结束输入。
- 程序流程图:
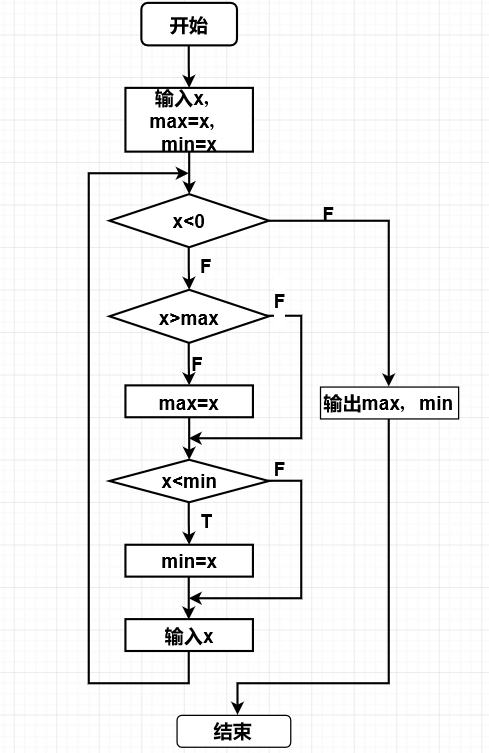
- 实验代码:
#include<stdio.h>
#include<conio.h>
main()
{
float x,max,min;
printf("please input scores:");
scanf("%f",&x);
max=min=x;
while(x>=0)
{
if(x>max) max=x;
if(x<min) min=x;
scanf("%f",&x);
}
printf("\nmax=%f\nmin=%f\n",max,min);
}
- 问题分析:
这道题是从键盘上输入分数,与当前最大值、最小值进行比较,然后根据输入的数字不断更新最大值与最小值,并用while循环判断输入的数字是否正确,若分数为负数则退出while循环。一开始我没有仔细分析课本中给出的流程图,填的是while(x<0),结果如下所示: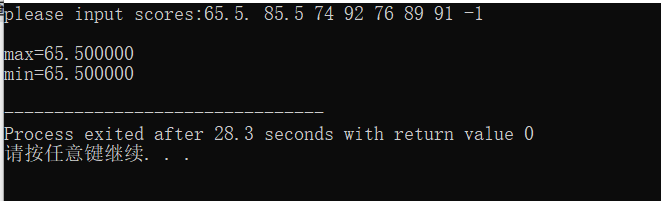
后面分析了一下这个程序的流程,发现应该填while(x>=0),才会执行相互比较大小的指令。 - 程序运行结果如下:
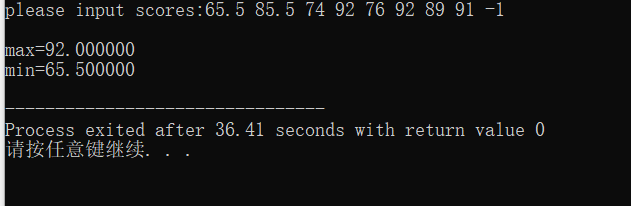
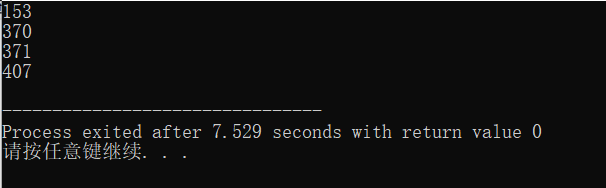
实验练习2: - 问题的简单描述:求所有的水仙花数(水仙花数是一个三位数的自然数,该数各位数的立方等于该数本身,如153为水仙花数13+53+3^3=153)。
- 程序流程图:
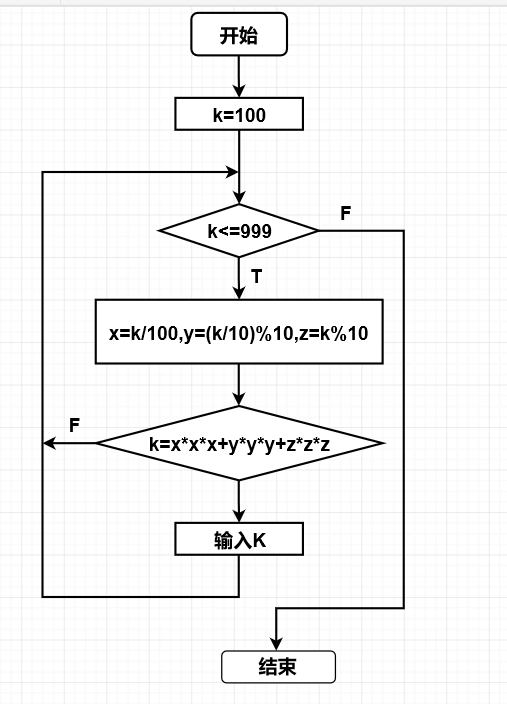
- 实验代码:
#include<stdio.h>
main()
{
int x,y,z;
int k=100;
while(k>=100&&k<=999)
{
x=k/100;
y=(k/10)%10;
z=k%10;
if(k==x*x*x+y*y*y+z*z*z)
printf("%d\n",k);
k++;
}
}
- 问题分析:(重点分析在实验过程中出现的问题,及解决方法。)
由问题描述中的水仙花数是一个三位数的自然数,该数各位数的立方和等于该数本身,可以得出两个重要的条件水仙花数的范围介于100和999之间,当该数各位数的立方和等于该数本身时才是水仙花数。刚开始做这个程序的时候我没想到是100到999之间的数,只输了个小于999,结果和书上的大不相同,后来又仔细研究了一下这道题才得以运行成功。 - 程序运行结果如下:
5.3.3:用do-while语句实现循环
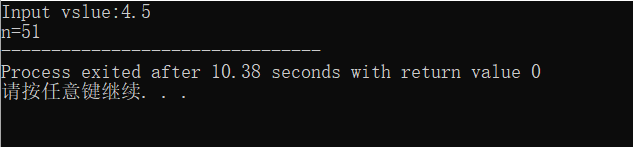
实验练习:求不等式
- 问题的简单描述:求满足1+1/2+1/3+...+1/n>value这个不等式的n最小值,其中,value是大于1的任何数。
- 程序流程图:

- 实验代码:
#include<stdio.h>
main()
{
float sum,value;
int n;
printf("Input vslue:");
scanf("%f",&value);
sum=0.0;
n=0;
do{
++n;
sum+=1.0/(float)n;
}
while(sum<value);
printf("n=%d",n);
}
3问题分析:(重点分析在实验过程中出现的问题,及解决方法。)
这道题是要求满足1+1/2+1/3+...+1/n>value这个不等式的n最小值,由于不等式的数值是大于1的任何数,所以用float型定义,利用do/while循环计算出不等式左边的每一项,并求出各项之和,切求出的和的值要大于value的值。
- 程序运行如下:
5.3.4:用while语句和for语句配合实现循环
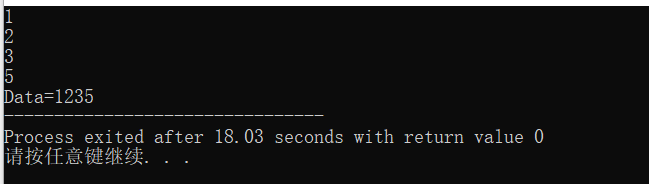
实验练习:十进制转换
- 问题的简单描述:输入4个数字字符,并将其转化为4位十进制整数后显示出来。
- 程序流程图:

- 实验代码:
#include<stdio.h>
main()
{
char c;
int k,data;
data=0;
for(k=0;k<4;k++)
{
while(1)
{
c=getchar();
if(c>='0'&&c<='9')
break;
}
/*将数字字符转化为对应的十进制整数,并形成4位数*/
if(k==0) data+=(c-'0')*1000;
if(k==1) data+=(c-'0')*100;
if(k==2) data+=(c-'0')*10;
if(k==3) data+=(c-'0');
}
printf("Data=%d",data);
}
- 问题分析:(重点分析在实验过程中出现的问题,及解决方法。)
这道题需要利用for循环接收用户输入的4个数字字符。利用if语句进行判断,如果输入的字符是非数字字符,则继续接收键盘输入;否则,程序跳出本次循环,进行后续转换操作。最后,如果输入的字符为数字字符,则将其转换为对应的十进制整数,并形成4位数,输出最后的结果。 - 运行程序如下:
5.3.5:用for语句嵌套实现循环
实验练习1:白马百担问题
- 问题的简单描述:有100匹马,要驼100担货物,其中1匹大马可以驼3担,1匹中马可以驼两担,两匹小马可以驼1担,请问,大马、中马和小马可以有多少种组合。
- 程序流程图:
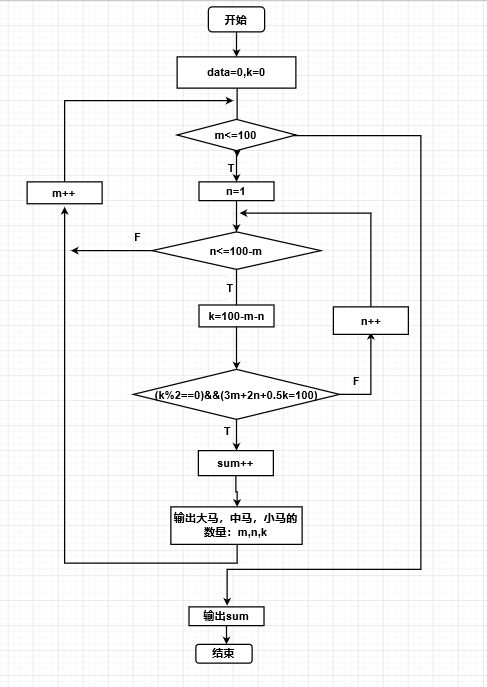
- 实验代码:
#include<stdio.h>
main()
{
int m,n,k;
int sum=0;
printf("各种驮法如下:\n");
for(m=1;m<=100;m++)
for(n=1;n<=100-m;n++)
{
k=100-m-n;/*大马、中马、小马满足的总匹数*/
if((k%2==0)&&(3*m+2*n+0.5*k==100))/*大马、中马、小马
驮货物满足的关系*/
{
printf("大马%3d匹;中马%3d匹;小马%3d匹.\n",m,n,k);
sum++;
}
}
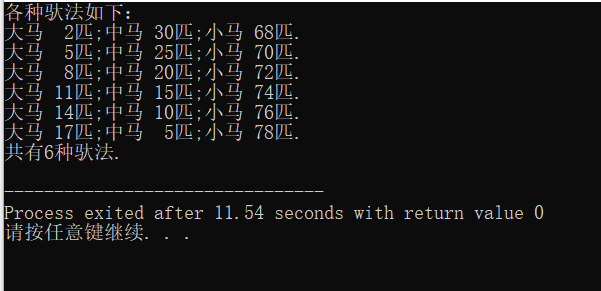
printf("共有%d种驮法.\n",sum);
}
- 问题分析:(重点分析在实验过程中出现的问题,及解决方法。)
要求出共有多少种驼法,找到大马、中马、小马满足的关系式,求出所有的解,解的个数就是所求的答案。首先先设3个整型变量用于记录大马、中马、小马的匹数,然后用嵌套for循环实现求大马、中马、小马的匹数,并找出三者之间所满足的关系式,最后用sum记录以上解的个数,输出结果。找到了三者之间所满足的关系式后要用if语句判断是否是一种解法,最后找到满足条件的全部解法。 - 运行结果如下:
实验练习2:求等差数列 - 问题的简单描述:编写程序,求一正整数等差数列的前6项的和,该数列前4项之和是26,前4项之积是880。
- 程序流程图:
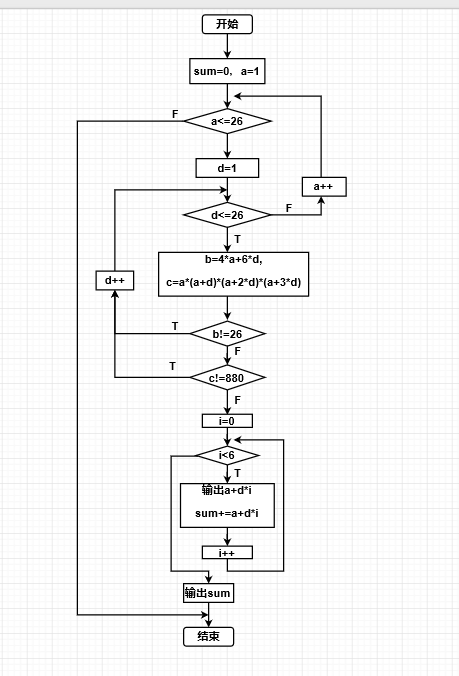
- 实验代码:
#include<stdio.h>
main()
{
int a,b,c,d,i,sum=0;
for(a=1;a<=26;a++)
for(d=1;d<=26;d++)
{
b=4*a+6*d;/*等差数列前4项之和*/
if(b!=26)
continue;
else
{
c=a*(a+d)*(a+2*d)*(a+3*d);/*等差数列前4项之积*/
if(c!=880)
continue;
else
for(i=0;i<6;i++)
{
printf("%d,",a+i*d);
sum=sum+(a+i*d);
}
}
}
printf("\n数列的前6项和:%d\n",sum);
}
- 问题分析:(重点分析在实验过程中出现的问题,及解决方法。)
这道题是求等差数列,等差数列是由首项和差值两项组成,用整型变量a,d分别记录该两项,接着利用for循环进行求解,并且需要满足数列前4项值之和为26,还必须满足数列前4项之积为880,得出a和d后,求出数列的前6项之和,最后输出结果。 - 运行结果如下:

实验练习3:食品分配问题 - 问题的简单描述:有30个学生一起买小吃,共花钱50元,其中,每个大学生花3元,每个中学生花2元,每个小学生花1元,问大、中、小学生的人数分配共有多少种不同的解(去掉某类学生数为0的解)?
- 程序流程图:
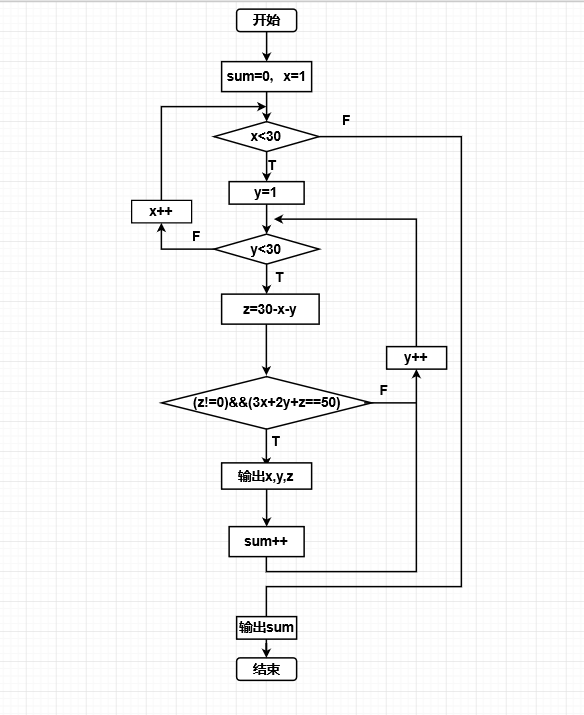
- 实验代码:
#include<stdio.h>
main()
{
int x,y,z,sum;
sum=0;
for(x=1;x<30;x++)
{
for(y=1;y<30;y++)
{
z=30-x-y;
if((z!=0)&&(3*x+2*y+z==50))
{
printf("大学生%3d\t中学生%3d\t小学生%3d\n",x,y,z);
sum=sum+1;
}
else
continue;
}
}
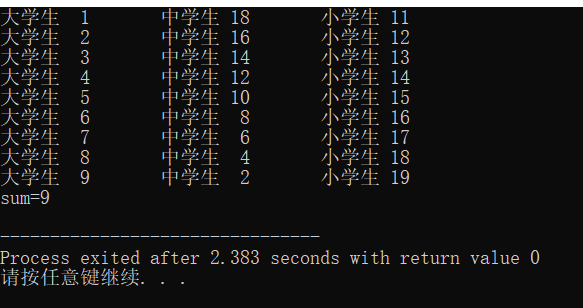
printf("sum=%d\n",sum);
}
- 问题分析:(重点分析在实验过程中出现的问题,及解决方法。)
这道题类似于百马百担的问题,要求有多少种食品分配的方法,找到大学生、中学生、小学生所满足的关系式,找出所有的解,解的个数就是所求的答案。首先先设4个整型变量分别代表大学生、中学生、小学生和解的个数,接着用嵌套for循环实现求大学生、中学生、小学生食品分配的各种方式,并找出三者之间所满足的关系式,用sum记录以上解的个数,输出sum的值。 - 运行结果如下:
三、实验小结(在本次实验中收获与不足)
这节实验课运行的程序只要跟着书上的流程图走,一步一步地将程序的代码写出,所有的问题都能迎刃而解,但是我们不能每次都靠书上给出的流程图,看到题目的时候应该先自己在脑子里思考一下这道题该怎么做,它的流程是怎么样的,思考完再看书上给出的流程图,和自己原先思考的有什么不一样的地方,如果不一样,自己思考的对不对,动手试试看能不能运行出来。另外,这节课的实验练习有点多,如果没有提前预习一下,可能会很难全部完成,所以,我们要养成课前预习的好习惯。



