小白1-I

 

 

 

 原文链接：https://blog.csdn.net/nobleman__/java/article/details/79597935

 还是不会 

 

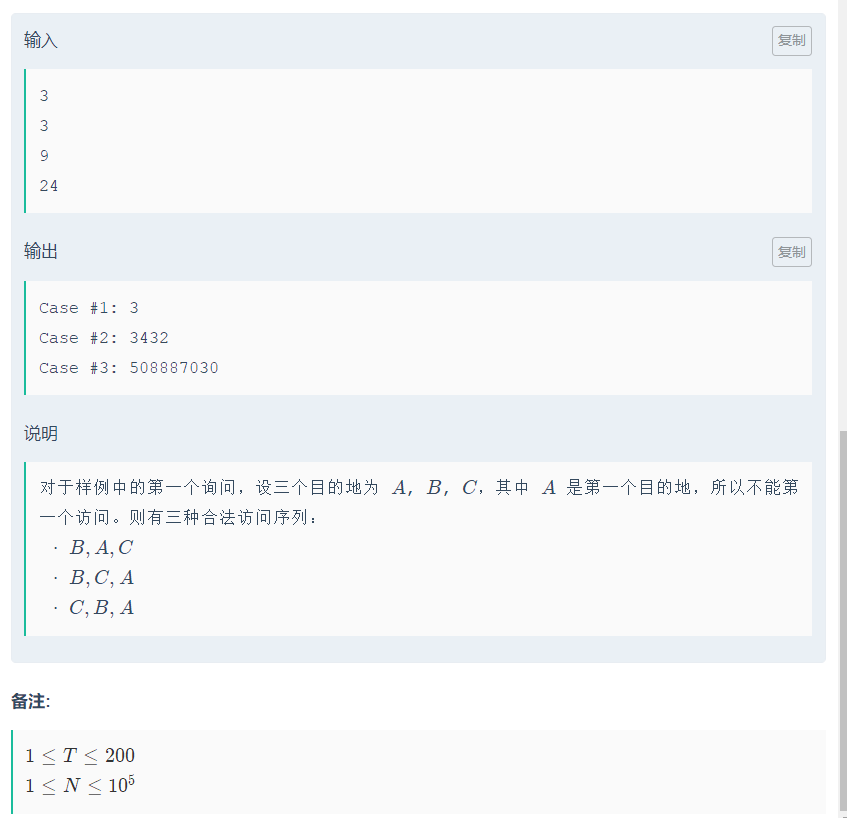
分析： 首先看到给的提示说了，第一个入栈的数不能先出，卡特兰数可以解决元素入栈出栈问题，我们可以根据递推公式，把1e5的卡特兰数打表，然后会发现题目上所求的为：k[n] - k[n - 1],因为通项公式为：
k[0] = k[1] = 1;
k[n] = k[n - 1] * (4 * n - 2) / (n + 1)

注意这里用到了取模，当然别忘了用逆元啦~

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10,MOD = 998244353;

 

///h(n)=h(n-1)*(4*n-2)/(n+1)

ll res[maxn];
#define mod(x) (x) % MOD

ll qpow(ll a, ll b) {
ll res = 1;
while (b) {
if (b & 1) res = (res * a) % MOD;
a = (a * a) % MOD;
b >>= 1;
}
return res;
}

void init() {
res[0] = 0;
res[1] = 1;
res[2] = 2;
for (int i = 2; i < maxn; i++) {
res[i] = (mod(mod(res[i - 1] * (4 * i - 2)) *1ll * qpow(i + 1, MOD - 2)) + MOD ) % MOD;
}
}

int main() {
int T;cin>>T;
init();
for (int i = 1; i <= T; i++) {
int n;cin>>n;
if (n == 1) cout<<0<<endl;
else cout<<"Case #"<<i<<": "<<(res[n] - res[n - 1] + MOD + MOD) % MOD<<endl;
}
return 0;
}