算法总结--动态规划
声明(
叠甲)：鄙人水平有限，本文为作者的学习总结，仅供参考。
1.动态规划介绍
动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。其中每一个状态一定是由上一个状态推导出来，这是DP的一个重要标志。
2.DP大法的使用
一般的来说，使用DP大法一般有以下几个重要的步骤
【1】 确定 DP 数组下标的含义
【2】 根据题意推导出递归公式（状态转移方程）
【3】 初始化 DP 数组，一般要进行边界处理，有时也会通过扩大数组的大小来避免边界的处理
【4】 遍历 DP 数组，并进行对应的更新
3.举些栗子
3.1 线性 DP —— 斐波那契数
题目如下:
题目描述
斐波那契数?（通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。
根据题目描述显然这个问题可以使用 DP 大法进行求解，且已给出了其状态转移方程 F(n) = F(n - 1) + F(n - 2)，以及对应的边界F(0) = 0，F(1)?= 1,于是我们就能够顺利写出对应的代码
int fib(int n)
{
if(n == 0) return 0;
if(n == 1) return 1;
int dp_n = 0;
int dp_n_1 = 1;
int dp_n_2 = 0;
for(int i = 0;i < n-1;i++)
{
dp_n = dp_n_1 + dp_n_2;
dp_n_2 = dp_n_1;
dp_n_1 = dp_n;
}
return dp_n;
}
3.2 二维 DP —— 过河卒
题目描述
棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示，A 点 (0, 0)、B 点 (n, m)，同样马的位置坐标是需要给出的。
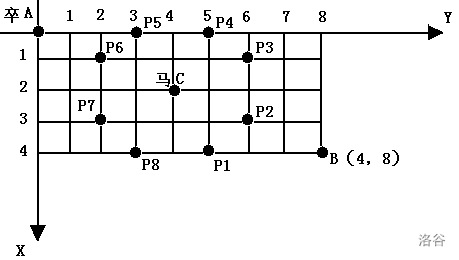
现在要求你计算出卒从 \(A\) 点能够到达 \(B\) 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。
该题可以说是不同路径问题的变种，根据题目描述，我们可以设卒到（x,y）处的方案有dp[x][y]种,又卒只能向下、或者向右，故可以推出其状态转移方程为dp[x][y]=dp[x-1][y]+dp[x][y-1]，接着是边界与特殊点(马的控制点)的处理,具体可以看代码的实现：
#include <bits/stdc++.h>
using namespace std;
int main()
{
int m,n,x_m,y_m;
cin >> n >> m >> x_m >> y_m;
long long int dp[n+1][m+1];
for(int i = 0;i <= n;i++)
{
for(int j = 0;j <= m;j++)
{
int d_m = (i-x_m)*(i-x_m) + (j-y_m)*(j-y_m); // 卒到马距离的平方
if(d_m == 5 || d_m == 0) dp[i][j] = 0;
else if(i == 0 && j == 0) dp[i][j] = 1; // 起点
else if(i == 0 && j != 0) dp[i][j] = dp[i][j-1]; // 上边界
else if(j == 0 && i != 0) dp[i][j] = dp[i-1][j]; // 左边界
else dp[i][j] = dp[i-1][j] + dp[i][j-1]; // 正常情况
}
}
cout << dp[n][m] << endl;
return 0;
}
3.2 四维 DP —— 方格取数
题目描述
设有 N 的方格图(N<9)，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 0。如下图所示（见样例）:
A
0 0 0 0 0 0 0 0
0 0 13 0 0 6 0 0
0 0 0 0 7 0 0 0
0 0 0 14 0 0 0 0
0 21 0 0 0 4 0 0
0 0 15 0 0 0 0 0
0 14 0 0 0 0 0 0
0 0 0 0 0 0 0 0
B
某人从图的左上角的 A 点出发，可以向下行走，也可以向右走，直到到达右下角的 B 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 0）。
此人从 A 点到 B 点共走两次，试找出 2 条这样的路径，使得取得的数之和为最大。
该题的难点在于有两条路线同时进行，但是思考清楚后还是很简单的，按照 DP 大法的步骤来
【1】 设两条路径分别到两点 (i,j)与(k,l)时的最大的数为 DP[i][j][k][l]
【2】 根据观察可以推得状态转移方程为 DP[i][j][k][l] = max(a,b), 其中 a，b 如下：
a = max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1])
b = max(dp[i][j-1][k-1][l],dp[i][j-1][k][l-1])
【3】 边界的处理，在此我们可以多申明出一个都为 0 的第 0 行与第 0 列
代码实现如下：
#include <bits/stdc++.h>
using namespace std;
int main()
{
int nums[10][10] = {0,};
int dp[10][10][10][10] = {0,};
int n = 0;
cin >> n;
while(1)
{
int x,y,a;
cin >> x >> y >>a;
if(x == 0 && y == 0 && a == 0) break;
nums[x][y] = a;
}
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= n;j++)
{
for(int k = 1;k <= n;k++)
{
for(int l = 1;l <= n;l++)
{
int a = max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1]);
int b = max(dp[i][j-1][k-1][l],dp[i][j-1][k][l-1]);
dp[i][j][k][l] = max(a,b) + nums[i][j] + nums[k][l];
if(i == k && j == l) dp[i][j][k][l] -= nums[i][j];
}
}
}
}
cout << dp[n][n][n][n];
return 0;
}
4.参考
本文到此结束，希望对您有所帮助。
