一、作业题目:
仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 (有理数是其分子、分母均为整数且分母不为零的分数)。
有理数基本运算:
- 构造有理数T,元素e1,e2分别被赋以分子、分母值
- 销毁有理数T
- 用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
- 将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
- 有理数T1,T2相加,结果存入有理数T3
- 有理数T1,T2相减,结果存入有理数T3
- 有理数T1,T2相乘,结果存入有理数T3
- 有理数T1,T2相除,结果存入有理数T3
二、实验要求:
- 抽象数据类型名为Rational。
- 有理数分母不能为负数或者0,类似输入请提示重输入。
- 数据对象和数据运算的表示与数据操作的实现分离。表示用头文件完成,实现用CPP文件完成。Main.cpp文件实现数据输入输出。
- 数据输入输出格式参考如下:
输入:
1 3 //T1的分子、分母
1 2 //T2的分子、分母
** 输出:**
5 6 //两个有理数相加
-1 6 //两个有理数相减
1 6 //两个有理数相乘
2 3 //两个有理数相除 - 程序应对异常输入或者出错必要处理和提示,比如提示:“分数是否需要约分等”。
三、博客作业:
1:作业内容
用ADT的抽象数据模型描述你的有理数数据类型。
ADT Rational{
数据对象:D={e1,e2|e1,e2都属于整型}
数据关系:R={<e1,e2>}
基本操作:
int get (int i) //输出
bool put (int i,int e) //赋值
int gcd (int x, int y) //最大公约数
int lcm (int x, int y) // 最小公倍数
Frac reduce (int e1, int e2) //自动化简分式
Frac operator+( Frac const &anthoer) // 加法
Frac operator-( Frac const &anthoer) // 减法
Frac operator*( Frac const &anthoer) // 乘法
Frac operator/( Frac const &anthoer) // 除法
}ADT Rational
数据结构,函数说明
1.头文件

2.函数及其功能
输出

赋值

最大公约数

最小公倍数

自动化简分式

加法

减法

乘法

除法

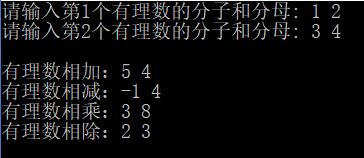
四、运行结果
正常情况
分母为零

负数

一正一负
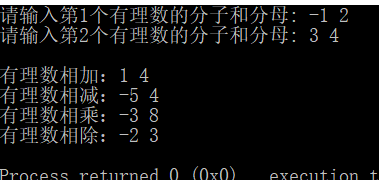
五、感想
1.通过这次作业,我学习到了不少东西,初步了解了数据结构是基于一组性质相同的值的集合以及定义在此集合上的一些操作的总称,而抽象数据类型相比较数据结构要具体一些,数据结构反映数据内部的构成方式,抽象数据类型需要通过固有数据类型来实现。
2.数据结构既有现实意义上的逻辑结构,也有计算机世界里的储存结构,抽象数据类型则由一种数据结构和在该数据结构上的一组操作组成。内容晦涩难懂,需要很大耐心。。。




