动态规划算法

动态规划常被认为是递归的反向技术，所谓的递归算法是从顶部开始，把问题向下全部分解为小的问题进行解决，直到解决整个问题为止。而动态规划则是从底部开始，解决小的问题同时把它们合并形成大问题的一个完整解决方案。

解决问题的递归算法经常是很优雅的，但是却是很低效的。尽管可能是优雅的计算机程序，但是C#语言编译器以及其他语言都不会把递归代码有效翻译成机器代码，并最终导致效率低下。

许多用递归解决的编程问题可以使用动态规划进行重新编写。动态规划通常会使用缓存对象，将不同的子解决方案存储起来，将中间运算结果记录下来，从而大大提高了效率。实际上就是使用了空间换时间的办法。

下面来看看一个递归算法的例子求斐波列数：

static void Main(string[] args)
        {
            Program p = new Program();
            int n = 6;
            int res = p.Fib(n);
           
            Console.WriteLine("Fib_{0}={1},调用次数为 {2}", n, res, p.numCalls);
            Console.ReadKey();
        }

private int numCalls = 0;
        private int Fib(int n)
        {
            numCalls++;
            Console.WriteLine("Fib调用 {0}", n);
            if(n<=1)
            {
                return 1;
            }
            else
            {
                return Fib(n - 1) + Fib(n - 2);
            }
        }

 

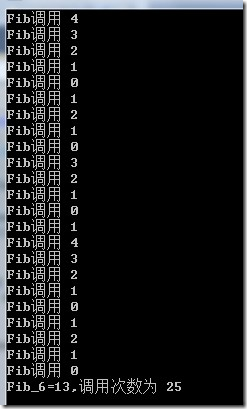
这个是我们通常的做法，直接使用递归，简单而优雅。

计算结果显示，计算6的斐波列数，调用次数为25次。

下面看看是动态规划的调用次数：

 

static void Main(string[] args)
        {
            Program p = new Program();
            int n = 6;
            int res = p.FibL(n);
           
            Console.WriteLine("Fib_{0}={1},调用次数为 {2}", n, res, p.numCalls);
            Console.ReadKey();
        }

  private int FastFib(int n, Dictionary<int, int> memo)
        {
            numCalls++;
            Console.WriteLine("Fib调用 {0}", n);
            if(!memo.ContainsKey(n))
            {
                memo.Add(n, FastFib(n - 1, memo) + FastFib(n - 2, memo));
            }
            return memo[n];
           
        }

        private int FibL(int n)
        {
            Dictionary<int, int> memo = new Dictionary<int, int>();
            memo.Add(0, 1);
            memo.Add(1, 1);
            return FastFib(n, memo);
        }

 

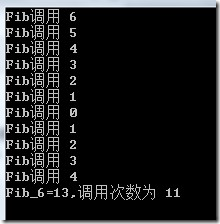
使用动态规划调用次数为11次。

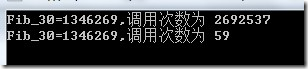
为了测试效率，我们把数值改了30，同时注释掉调用过程的打印代码

结果显示，动态规划比递归有很大的效率提高。

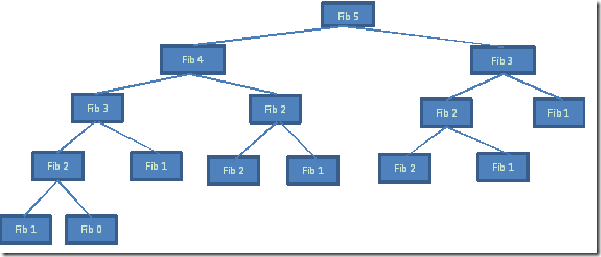
递归的效率极低的，看看如下图中树就可以明确地知道递归算法的效率是多么的低

 

 

递归算法的问题在于递归过程中会重复计算太多的数值。如果编译器可以跟踪已经计算过的数值，那么这个函数就几乎不会如此低效了。利用动态规划技术来设计算法会比递归算法高效许多。

使用动态规划技术设计算法从解决最简单的可解子问题开始入手，利用解决方案解决更加复杂的子问题直到接近整个问题为止。每个子问题的解决方案存储在缓存中，从而减少很多重复运算，大大提高效率。递归数越大，动态规划的效率相对递归来说，优势越明显。