[机器学习] sklearn聚类

聚类（Clustering）简单来说就是一种分组方法，将一类事物中具有相似性的个体分为一类，将另一部分比较相近的个体分为另一类。例如人和猿都是灵长目动物，但是根据染色体数目不同可以将人和猿分类不同的两类。虽然人根据肤色又可以分为黄种人，白种人，有色种人，但是根据行为举止和形态，往往把黄种人，白种人等归于人这一大类。

K-Means 算法

K-Means算法是聚类中一种非常常用的算法。具体步骤如下：

1. 从n个对象中任意选择k个对象作为初始聚类中心
2. 计算每个对象计算与这k个初始聚类中心的距离。
3. 经过步骤2的计算，各个对象都与这k个聚类中心都有一个距离。对于某个对象将其和距离其最近的初始聚类中心归为一个类簇。
4. 重新计算每个类簇的聚类中心的位置。
5. 重复3，4两个步骤，直到每次计算发生类簇变化的对象数量较少时结束分类。

K-Means算法中，需要实现确定有： 初始聚类中心的数量，距离计算公式（曼哈顿距离，欧氏距离），类簇的数量。

sklearn基础代码

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
 
#15个点
x1 = np.array([1, 2, 3, 2, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
x2 = np.array([1, 3, 2, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('Sample')
#查看15个点的分布
plt.scatter(x1, x2)
plt.show()

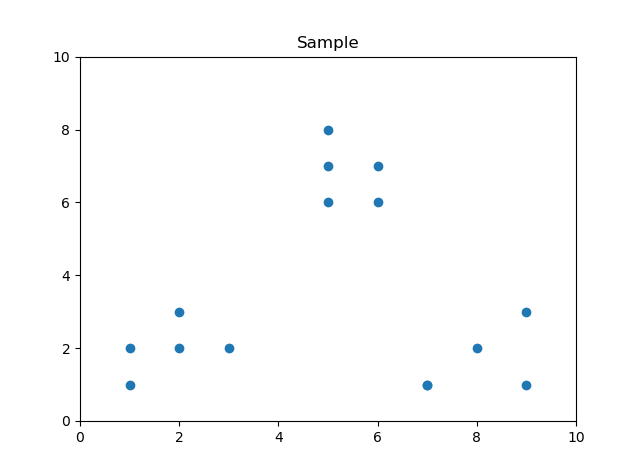
上面代码首先获得15个点，15个点分布如下图所示：

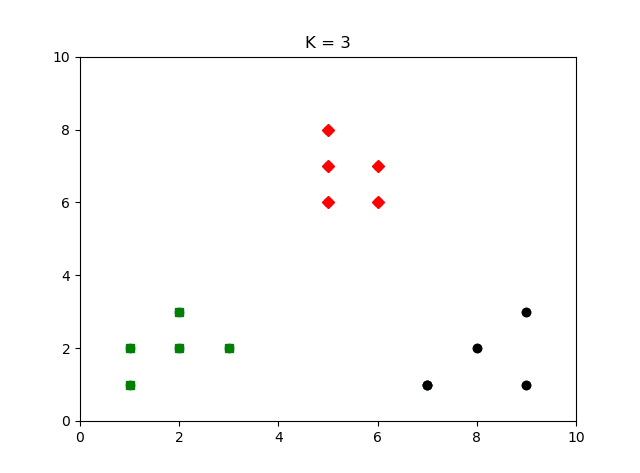
然后将15个点分为3个类簇，并用黑色，绿色，红色标记各个类簇中的点。对于sklearn中用KMeans函数进行聚类，其他用默认参数便可获得较好分类效果。KMeans其他参数改动可参考官网文档：sklearn.cluster.KMeans

#类簇的数量
clusters=3
 
#聚类
kmeans_model = KMeans(n_clusters=clusters).fit(X)
#打印聚类结果
print('聚类结果：', kmeans_model.labels_) #聚类结果： [1 1 1 1 1 0 0 0 0 0 2 2 2 2 2]
#画图
colors = ['black', 'green', 'red']  
markers = ['o', 's', 'D']  
 
for i, l in enumerate(kmeans_model.labels_):  
    plt.plot(x1[i], x2[i], color=colors[l],marker=markers[l],ls='None')  
    plt.xlim([0, 10])  
    plt.ylim([0, 10])  
    plt.title('K = %s' %(clusters)) 
plt.show()

分类结果：

层次聚类

层次聚类（Hierarchical Clustering）是指通过聚类算法将样本分为若干的大类簇，然后将大类簇分为若干个小类簇。最后形成类似一棵树的结构。例如大学里面可以分为若干学院，学院又可分为若干的系。sklearn中对应的算法函数为cluster.AgglomerativeClustering函数。该函数有三种策略：

• Ward策略：以所有类簇中的方差最小化为目标
• Maximum策略： 以各类簇之间的距离最大值最小化为目标
• Average linkage策略： 以各类簇之间的距离的平均值最小化为目标

函数使用为：

model = AgglomerativeClustering(linkage='ward',n_clusters=clusters).fit(X)

其中linkage为策略选择参数，函数其他参数改动可参考官网文档：sklearn.cluster.AgglomerativeClustering。具体例子见sklearn Hierarchical Clustering。

密度聚类

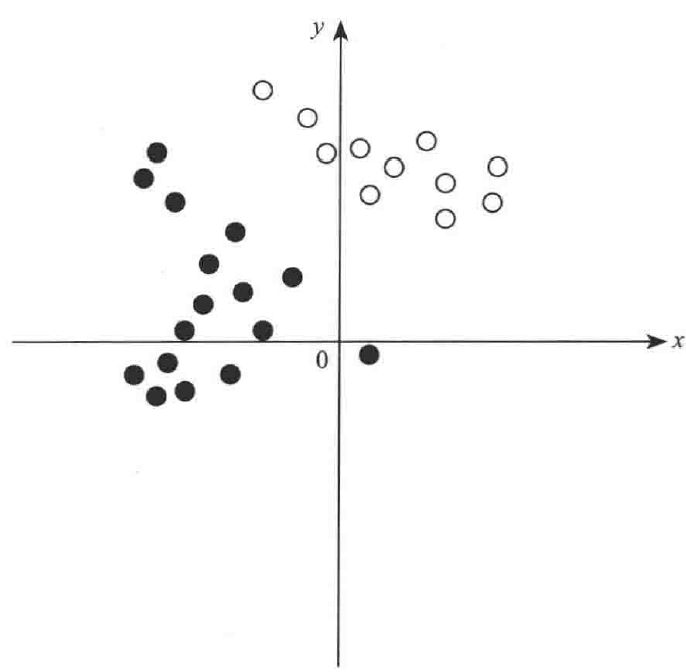
密度聚类适用于聚类形状不规则的情况，如下图所示：

通常在这种情况，K-Means算法往往聚类效果较差。因此通过密度聚类能够很好的解决这种情况。具体算法见用scikit-learn学习DBSCAN聚类

sklearn中进行密度聚类的函数为cluster.DBSCAN。函数使用为：

DBSCAN(eps=2000, min_samples=1).fit(X)

其中eps是指设定的阈值，在算法进行时，如果在这个范围内找不到对象，则认为所操作的类簇确认完毕。

min_sample是指类簇最小应该有多少个点。如果小于该数字，则会将对象总数小于该数字的类簇视为噪声点，在结果中直接丢弃。函数其他参数改动可参考官网文档：sklearn.cluster.DBSCAN。

聚类评估

聚类的质量评估主要有最佳类簇数的确定和聚类效果评价。

最佳簇数确定

最佳簇数的确定主要有两种方法：经验法和肘方法。

1. 经验法，主要指对于含有n个对象的空间，最佳簇数为

\[\sqrt{\frac{n}{2}} \]

但是该方法没有太多理论依据，实际应用只能作为参考。

2. 肘方法是目前用的较多的确定最佳簇数的方法。具体方法如下：

• 将包含n个对象的对象空间分为m个簇类（m位于[0, n]），计算这m个类簇各自的空间中心点（空间重心）在哪。
• 计算m个类簇中每个类簇中每个对象与该类簇重心的距离的和，最后把m个类簇各自的距离和相加得到和函数。
• 确定m遍历[0，n]之间的值，当增加一个簇类时距离的变化没有前一个分类距

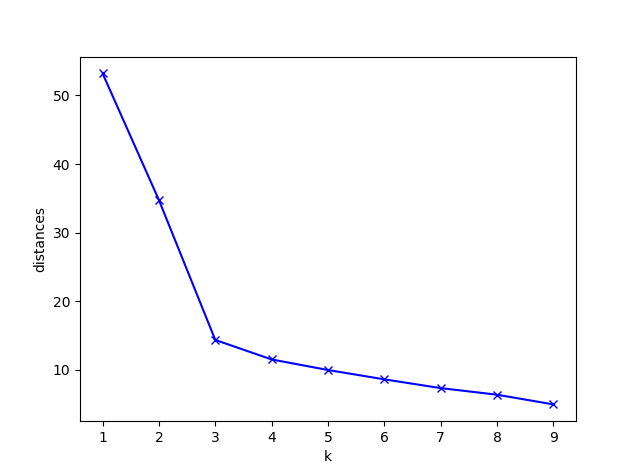
如下图所示，m从1次、2次逐渐增加，整个曲线的斜率迅速下降，下降过程会出现拐点，使得曲线变得平滑。图中当m取为3或4的时候，都可以被认为是最佳类簇数。由于聚类是一种无监督学习的方法，该方法很多时候拐点较难确定，适当选择就好。

上图的python代码如下所示：

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
 
#15个点
x1 = np.array([1, 2, 3, 2, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
x2 = np.array([1, 3, 2, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
 
#类簇的数量1到9
clusters = range(1, 10) 
#距离函数
distances_sum = []
 
for k in clusters:
    kmeans_model = KMeans(n_clusters = k).fit(X)
    print('类簇中心的坐标点: ', kmeans_model.cluster_centers_ ) #类簇中心大小为(k, 2)
    #计算各对象离各类簇中心的欧氏距离，生成距离表，大小为(15， k)
    distances_point = cdist(X, kmeans_model.cluster_centers_, 'euclidean')
    #提取每个对象到其类簇中心的距离（该距离最短，所以用min函数），并相加。
    distances_cluster = sum(np.min(distances_point,axis=1))
    #依次存入range(1, 12)的距离结果
    distances_sum.append(distances_cluster)
 
 
plt.plot(clusters, distances_sum, 'bx-')
plt.xlabel('k')
plt.ylabel('distances')
plt.show()

其中cdist函数为距离计算函数，上述代码用的是欧氏距离。具体函数使用见：scipy.spatial.distance.cdist

聚类质量测定

目前测定聚类质量的方法很多，常用的是使用轮廓系数进行。轮廓函数定义如下：

\[s(v)=\frac{b(v)-a(v)}{max[a(v),b(v)]} \]

上述公式对于某对象v来说，a(v)为v到本类簇中其他各点距离的平均值，b(v)为v到其他类簇的最小平均值（从其他各类簇中取一个离v最近的对象，计算距离）。一般s(v)在-1到1之间。当s(v)接近1，表明v的类簇非常紧凑，s(v)接近-1，表明聚类效果不好。s(v)越接近1越好，但是要考虑计算成本。

sklearn具体实例如下

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn import metrics
 
#15个点
x1 = np.array([1, 2, 3, 2, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
x2 = np.array([1, 3, 2, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
 
plt.figure()
plt.subplot(2,2,1) #将图像分为2行2列，现在是第一个子图进行绘图
 
plt.title('Sample')
plt.scatter(x1, x2)
 
colors =['black', 'green', 'red', 'yellow', 'blue', 'gray', 'purple']
markers =['o', 's','D', 'v', 'p', '+', '*' ]
clusters=[3, 4, 7] #类簇数
suplot_counter =1 #画板位置
for k in clusters:
    suplot_counter += 1
    plt.subplot(2, 2, suplot_counter)
    kmeans_model = KMeans(n_clusters=k).fit(X)
    for i, l in enumerate(kmeans_model.labels_):
        plt.plot(x1[i], x2[i], color=colors[l],marker=markers[l],ls='None')  
        score = metrics.silhouette_score(X, kmeans_model.labels_, metric='euclidean')
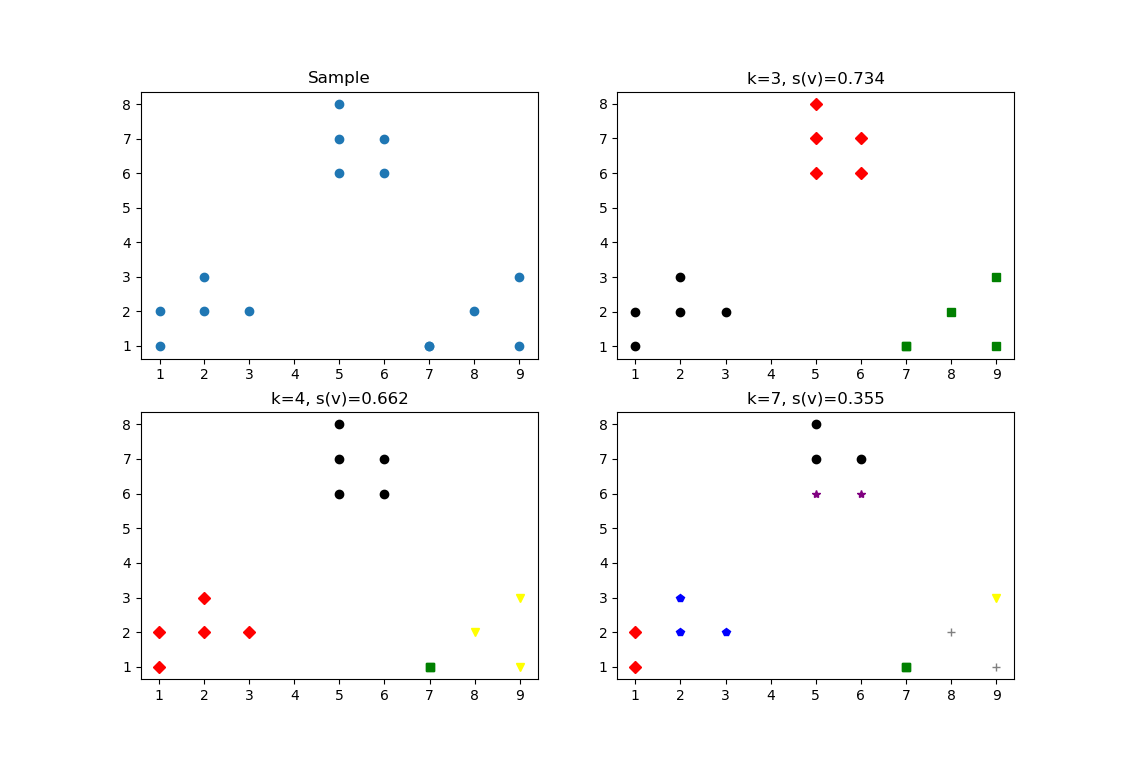
        plt.title('k=%s, s(v)=%.03f' %(k, score))

由上图可以知道当k=3轮廓稀疏最大，k=4其次。代码中metrics.silhouette_score为轮廓评价函数，具体见官方文档：

sklearn.metrics.silhouette_score