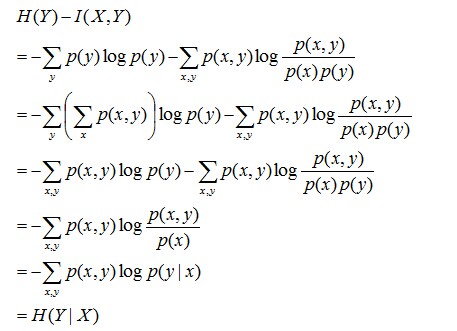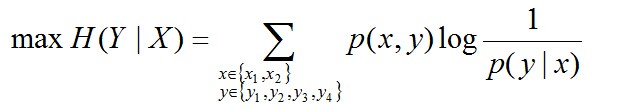[数学理论] 最大熵模型

转载于http://blog.csdn.net/lg1259156776/

最大熵模型总结

摘要

本文对最大熵模型进行了系统性的学习和总结，从不同的角度来解读熵的概念以及最大熵的内涵。对最大熵的具体应用进行了梳理，并介绍了与最大熵相关的一些概念，最后通过一个简单的demo来对最大熵模型进行直观的认识和感悟。

引言

熵，忘了第一次接触是在物理课上还是在化学课上，总之是描述系统的无序性或者混乱状态，跟热力学第二定律的宏观方向性有关：在不加外力的情况下，总是往混乱状态改变；跟化学反应的方向性有关，总是往能量降低的方向改变。印象中，熵总是与能量与混乱状态联系在一起。最近读吴军的《数学之美》最大熵一章节，对于这个最大熵模型有了重新的认识，同时由于在近期的学术论文研究中需要借助最大熵进行决策，因此才促成此次对最大熵模型的总结。

统计建模方法是用来modeling随机过程行为的。在构造模型时，通常供我们使用的是随机过程的采样，也就是训练数据。这些样本所具有的知识（较少），事实上，不能完整地反映整个随机过程的状态。建模的目的，就是将这些不完整的知识转化成简洁但准确的模型。我们可以用这个模型去预测随机过程未来的行为。

在统计建模这个领域，指数模型被证明是非常好用的。因此，自世纪之交以来，它成为每个统计物理学家们手中不可或缺的工具。最大熵模型是百花齐放的指数模型的一种，它表示的这类分布有着有趣的数学和哲学性质。尽管最大熵的概念可以追溯到远古时代，但直到近年来计算机速度提升之后，才允许我们将最大熵模型应用到统计评估和模式识别的诸多现实问题中（最大熵才在现实问题上大展身手）。

熵的概念

物理学的熵

描述事物无序性的参数，熵越大则无序性越强。从宏观方面讲（根据热力学定律），一个体系的熵等于其可逆过程吸收或耗散的热量除以它的绝对温度。从微观讲，熵是大量微观粒子的位置和速度的分布概率的函数。

自然界的一个基本规律就是熵递增原理，即，一个孤立系统的熵，自发性地趋于极大，随着熵的增加，有序状态逐步变为混沌状态，不可能自发地产生新的有序结构，这意味着自然界越变越无序。实际上就是热力学第二定律。

信息论的熵

熵

在物理学中，熵是描述客观事物无序性的参数。信息论的开创者香农认为，信息（知识）是人们对事物了解的不确定性的消除或减少。他把不确定的程度称为信息熵。设随机变量ξ，他有A1、A2….An共n个不同的结果，每个结果出现的概率为p1，p2….pn，那么ξ的不确定度，即信息熵为：

<span style="display:inline-block; position:relative; width:15.652em; height:0px; font-size:125%"><span style="position:absolute; top:-2.698em; left:0.003em"><span class="mrow" id="MathJax-Span-2"><span class="mi" id="MathJax-Span-3" style="font-family:MathJax_Math-italic">H<span style="display:inline-block; overflow:hidden; height:1px; width:0.053em"> (ξ) = \sum i = 1 n p i log 1 p i = - \sum i = 1 n p i log p i

熵越大，越不确定。熵为0，事件是确定的。例如抛硬币，每次事件发生的概率都是1/2的话，那么熵=1： H(X)=−(0.5log0.5+0.5log0.5)=1。

联合熵

两个随机变量X，Y的联合分布，可以形成联合熵Joint Entropy，用H(X,Y)表示。

条件熵

有时候我们知道x,y变量不是相互独立的，y的作用会影响x的发生，举个例子就是监督学习了，有了标记y之后肯定会对x的分布有影响，生成x的概率就会发生变化，x的信息量也会变化。那么此时X的不确定度表示为：

<span style="display:inline-block; position:relative; width:15.953em; height:0px; font-size:125%"><span style="position:absolute; top:-2.698em; left:0.003em"><span class="mrow" id="MathJax-Span-81"><span class="mi" id="MathJax-Span-82" style="font-family:MathJax_Math-italic">H<span style="display:inline-block; overflow:hidden; height:1px; width:0.053em"> (X | Y) = \sum (x, y) \in X \times Y p (x, y) log 1 p ( x | y )

这个其实就是条件熵Conditional Entropy。很显然，Y加入进来进行了标记之后，就引入了知识了，所以会减小X的不确定性，也就是减小了熵。所以知识能够减小熵。
比如在自然语言的统计模型中，一元模型就是通过某个词本身的概率分布来消除不确定因素；而二元及更高阶的语言模型则还使用了上下文的信息，那就能准确预测出一个句子中当前词汇。在数学上可以严格地证明为什么这些相关的信息也能够用来消除不确定性，下面的公式就表明了这个性能：

<span style="display:inline-block; position:relative; width:7.403em; height:0px; font-size:125%"><span style="position:absolute; top:-2.698em; left:0.003em"><span class="mrow" id="MathJax-Span-127"><span class="mi" id="MathJax-Span-128" style="font-family:MathJax_Math-italic">H<span style="display:inline-block; overflow:hidden; height:1px; width:0.053em"> (X) \geq H (X | Y)

当多了Y的信息之后，关于X的不确定性下降了，在自然语言统计模型中，如果把Y看成是前一个字，那么在数学上就证明了二元模型应该比一元模型要好。同理，可以定义两个条件的条件熵，如下公式：

<span style="display:inline-block; position:relative; width:20.503em; height:0px; font-size:125%"><span style="position:absolute; top:-2.698em; left:0.003em"><span class="mrow" id="MathJax-Span-142"><span class="mi" id="MathJax-Span-143" style="font-family:MathJax_Math-italic">H<span style="display:inline-block; overflow:hidden; height:1px; width:0.053em"> (X | Y, Z) = \sum (x, y, z) \in X \times Y \times Z p (x, y, z) log 1 p ( x | y , z )

还可以证明 H(X|Y)≥H(X|Y,Z)，也就是说三元模型要比二元模型好些。

一个有趣的问题是：上述式子等号什么时候成立？等号成立说明了增加了信息，但是不确定性却没改变，这说明获取的信息对于要研究的事物丝毫没有关系。也就是说在概率是统计独立的。

相对熵

又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度等。设p(x)、q(x)是X中取值的两个概率分布（x为在X这个随机变量中取值），则p对q的相对熵是
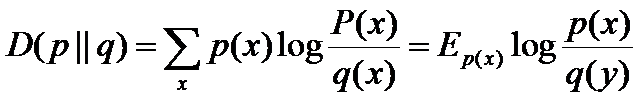
这里写图片描述
在一定程度上，相对熵可以度量两个随机变量的“距离”，且有D(p||q) ≠D(q||p)。
相对熵有如下的三条结论：

对于两个完全相同的概率分布函数，它们的相对熵为0；

相对熵越大，两个概率分布函数的差异性越大；反之，相对熵越小，两个概率分布函数的差异性越小。

对于概率分布或者概率密度函数，如果取值均大于0，相对熵可以用来度量两个随机分布的差异性。

上面提到了相对熵是不对称的，有D(p||q) ≠D(q||p)，这样使用起来不方便，詹森和香农提出了一种新的相对熵计算方法，将上面的不等式两边取平均，如下：

<span style="display:inline-block; position:relative; width:16.652em; height:0px; font-size:125%"><span style="position:absolute; top:-2.698em; left:0.003em"><span class="mrow" id="MathJax-Span-219"><span class="mi" id="MathJax-Span-220" style="font-family:MathJax_Math-italic">J<span style="display:inline-block; overflow:hidden; height:1px; width:0.102em"> S (q (x) | | p (x)) = 1 2 (D (p | | q) + D (q | | p))

相对熵最早是用在信号处理上，如果两个随机信号相对熵越小，说明这两个信号越接近，否则信号的差异性越大。后来研究信息处理的学者们用来衡量两段信息的相似程度，比如说如果一篇文章是照抄或者改写另一篇，那么这两篇文章中词频分布的相对熵就非常小，接近于0。
相对熵在自然语言处理中还有很多应用，比如用来衡量两个常用词（在语法和语义上）不同文本中的概率分布，看它们是否同义。另外，利用相对熵，还可以得到信息检索中最重要的一个概念：词频率-逆向文档频率（TF-IDF）。

互信息

两个随机变量X，Y的互信息，定义为X，Y的联合分布和独立分布乘积的相对熵，用表示I(X,Y)
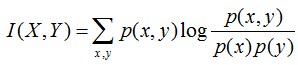
这里写图片描述
且有I(X,Y)=D(P(X,Y) || P(X)P(Y))。计算下H(Y)-I(X,Y)的结果，如下：

通过上面的计算过程，发现有H(Y)-I(X,Y) =H(Y|X)。故通过条件熵的定义，有：H(Y|X) = H(X,Y) - H(X)，而根据互信息定义展开得到H(Y|X) = H(Y) - I(X,Y)，把前者跟后者结合起来，便有I(X,Y)= H(X) + H(Y) - H(X,Y)，此结论被多数文献作为互信息的定义。

关于互信息，参考《数学之美》，想再多说几句：
当获取的信息和要研究的事物“有关系”时，这些信息才能用来帮助消除不确定性。比如常识告诉我们，随机事件“今天北京下雨”与另一个随机变量“过去二十四个小时北京空气湿度”的相关性就很大，但是到底有多大呢？再比如，“过去二十四个小时北京空气湿度”与“旧金山的天气”似乎就相关性不大，如何度量这种相关性呢？香农提出了互信息（Mutual Information）作为两个随机事件相关性的度量。

<span style="display:inline-block; position:relative; width:20.453em; height:0px; font-size:125%"><span style="position:absolute; top:-2.698em; left:0.003em"><span class="mrow" id="MathJax-Span-270"><span class="mi" id="MathJax-Span-271" style="font-family:MathJax_Math-italic">I<span style="display:inline-block; overflow:hidden; height:1px; width:0.053em"> (X; Y) = H (X) - H (X | Y) = H (Y) - H (Y | X)

现在清楚了，所谓两个事件相关性的量化度量，就是在了解其中一个Y的前提下，对消除另一个X不确定性所提供的信息量。当X和Y完全不相关时，取值为0，也就是前面所讲的等号成立的条件；而当X和Y完全相关时，取值为1。

熵编码

熵编码即编码过程中按熵原理不丢失任何信息的编码。信息熵为信源的平均信息量（不确定性的度量）。常见的熵编码有：香农(Shannon)编码、哈夫曼(Huffman)编码和算术编码(arithmetic coding)。
其中哈夫曼编码可以参看我的另一篇博文《数据结构（三）:非线性逻辑结构-特殊的二叉树结构：堆、哈夫曼树、二叉搜索树、平衡二叉搜索树、红黑树、线索二叉树》中有着详细而且精彩地论述。

熵和主观概率

因为熵用概率表示，所以这涉及到主观概率。概率用于处理知识的缺乏（概率值为1表明对知识的完全掌握，这就不需要概率了），而一个人可能比另一个人有着更多的知识，所以两个观察者可能会使用不同的概率分布，也就是说，概率（以及所有基于概率的物理量）都是主观的。在现代的主流概率论教材中，都采用这种主观概率的处理方法。

熵的性质

当所有概率相等时，熵取得最大值

上面关于熵的公式有一个性质：假设可能状态的数量有限，当所有概率相等时，熵取得最大值。
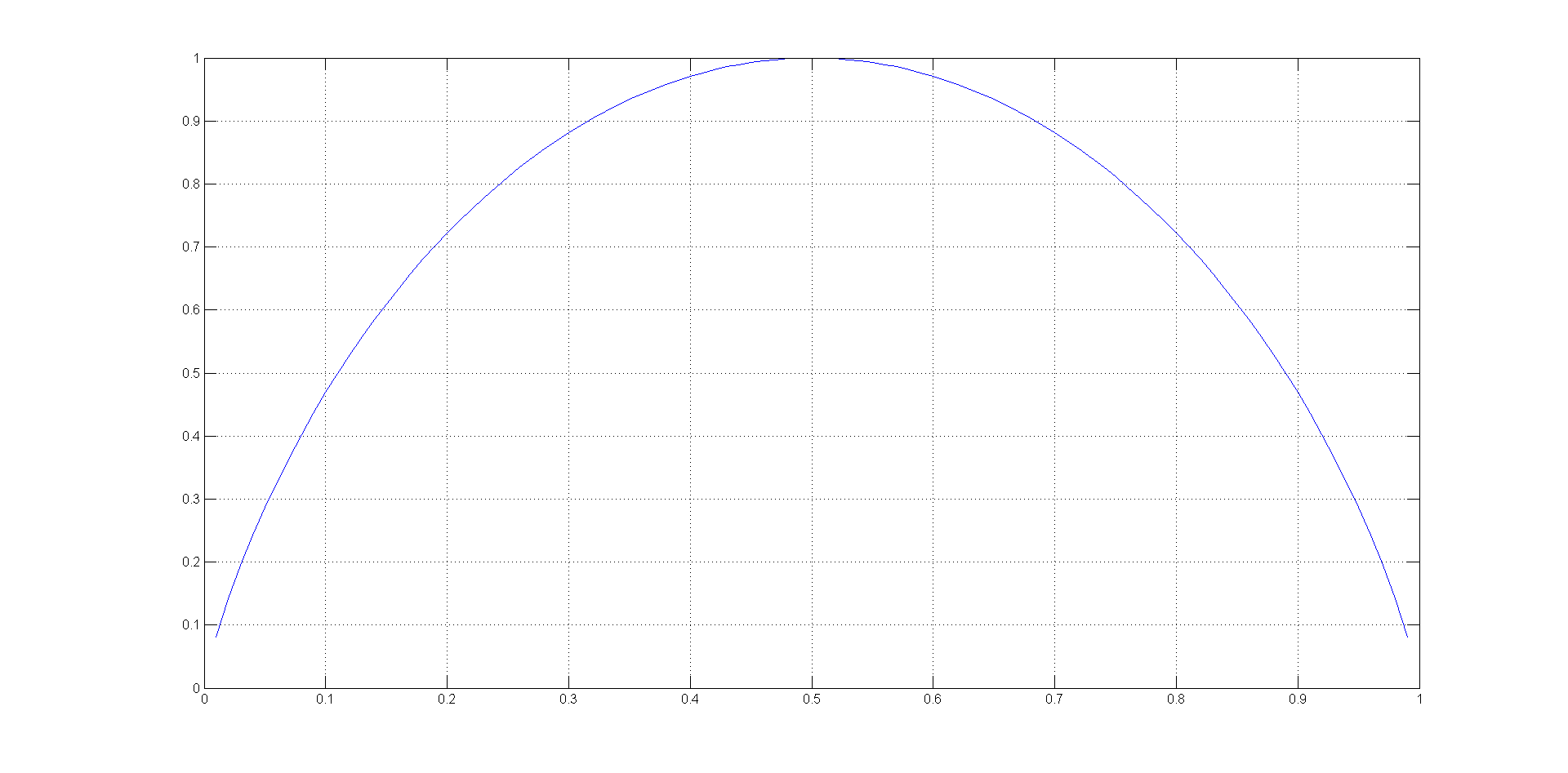
在只有两个状态的例子中，要使熵最大，每个状态发生的概率都是1/2，如下图所示：

p=[0:0.01:1];
h=-1*(p.*log2(p)+(1-p).*log2(1-p));
plot(p,h); grid on;

这里写图片描述

小概率事件发生时携带的信息量比大概率事件发生时携带的信息量多

实际上信息量与人们的惊奇度是相关的，比如你认为湖人队夺冠的概率非常高，结果湖人队以大比分0：4被横扫出局了，这个消息让你感到很吃惊。实际上就是湖人队被0：4横扫这件事情的信息量非常大，你认为是属于小概率事件，认为它几乎不可能发生，但是它一旦发生了你就感到很吃惊。相反，当湖人队顺利夺冠，你就不会有什么惊奇的表情了。

最大熵原理

吴军《数学之美》中关于最大熵的论述

最大熵原理指出，当我们需要对一个随机事件的概率分布进行预测时，我们的预测应当满足全部已知的条件，而对未知的情况不要做任何主观假设。在这种情况下，概率分布最均匀，预测的风险最小。因为这时概率分布的信息熵最大，所以人们称这种模型叫“最大熵模型”。我们常说，不要把所有的鸡蛋放在一个篮子里，其实就是最大熵原理的一个朴素的说法，因为当我们遇到不确定性时，就要保留各种可能性。说白了，就是要保留全部的不确定性，将风险降到最小。

下面是吴军在AT&T实验室做最大熵模型报告时所进行的解释：

带去了一个色子，问听众”每个面朝上的概率分别是多少”，所有人都说是等概率，即各点的概率均为1/6。这种猜测当然是对的。我问听众们为什么，得到的回答是一致的：对这个”一无所知”的色子，假定它每一个朝上概率均等是最安全的做法。（你不应该主观假设它象韦小宝的色子一样灌了铅。）从投资的角度看，就是风险最小的做法。从信息论的角度讲，就是保留了最大的不确定性，也就是说让熵达到最大。接着，我又告诉听众，我的这个色子被我特殊处理过，已知四点朝上的概率是三分之一，在这种情况下，每个面朝上的概率是多少？这次，大部分人认为除去四点的概率是1/3，其余的均是 2/15，也就是说已知的条件（四点概率为1/3）必须满足，而对其余各点的概率因为仍然无从知道，因此只好认为它们均等。注意，在猜测这两种不同情况下的概率分布时，大家都没有添加任何主观的假设，诸如四点的反面一定是三点等等。（事实上，有的色子四点反面不是三点而是一点。）这种基于直觉的猜测之所以准确，是因为它恰好符合了最大熵原理。

实际上这个论述跟上面熵的性质相对应，在没有先验知识的情况下，对不同情况选择等概率是最安全的，也就是对应最大熵原理，数学描述为：

<span style="display:inline-block; position:relative; width:8.053em; height:0px; font-size:125%"><span style="position:absolute; top:-2.698em; left:0.003em"><span class="mrow" id="MathJax-Span-306"><span class="texatom" id="MathJax-Span-307"><span class="mrow" id="MathJax-Span-308"><span class="msubsup" id="MathJax-Span-309"><span style="display:inline-block; position:relative; width:0.953em; height:0px"><span style="position:absolute; top:-2.548em; left:0.003em"><span class="mi" id="MathJax-Span-310" style="font-family:MathJax_Math-italic">p * = arg max p H (p)

利用最大熵原理求解问题

一个快餐店提供3种食品：汉堡(B)、鸡肉(C)、鱼(F)。价格分别是1元、2元、3元。已知人们在这家店的平均消费是1.75元，求顾客购买这3种食品的概率。

如果你假设一半人买鱼另一半人买鸡肉，那么根据熵公式，这不确定性就是1位（熵等于1）。但是这个假设很不合适，因为它超过了你所知道的事情。我们已知的信息是：

<span style="display:inline-block; position:relative; width:16.852em; height:0px; font-size:125%"><span style="position:absolute; top:-3.948em; left:0.003em"><span class="mrow" id="MathJax-Span-326"><span class="mrow" id="MathJax-Span-327"><span class="mo" id="MathJax-Span-328" style="vertical-align:0.003em"><span style="font-family:MathJax_Size3">{<!-- -->p(B)+p(C)+p(F)=11∗p(B)+2∗p(C)+3∗p(F)=1.75

对前两个约束，两个未知概率可以由第三个量来表示，可以得到：

<span style="display:inline-block; position:relative; width:10.853em; height:0px; font-size:125%"><span style="position:absolute; top:-3.948em; left:0.003em"><span class="mrow" id="MathJax-Span-373"><span class="mrow" id="MathJax-Span-374"><span class="mo" id="MathJax-Span-375" style="vertical-align:0.003em"><span style="font-family:MathJax_Size3">{<!-- -->p(C)=0.75−2∗p(F)p(B)=0.25+p(F)

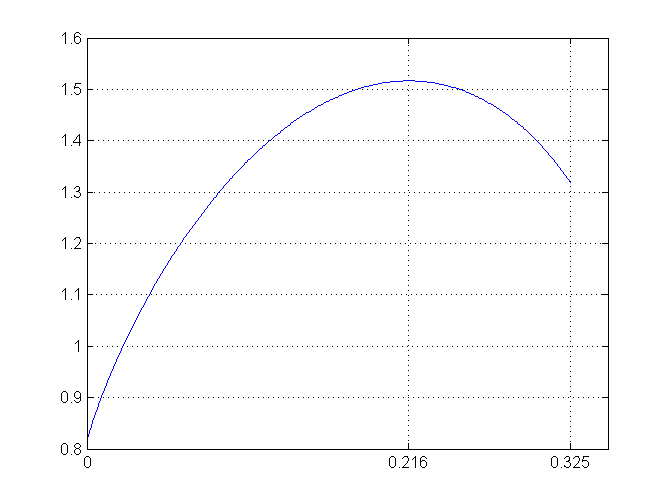
把上式代入熵的表达式中，熵就可以用单个概率 p(F) 来表示。对这个单变量优化问题，很容易求出 p(F)=0.216 时熵最大，有 p(B)=0.466, p(C)=0.318 和 S=1.517。

下面给出最为暴力的求解方式，在可行域内，遍历所有的频率，然后求出最大熵所对应的pF，之后就可以分别计算出pB，pC和S了。

%% 要保证pB，pC和pF都在0，1之间，pF的取值是约束的
%概率约束关系
pF = 0.001 : 0.001 : 0.325;
pB = 0.25 + pF;
pC = 0.75 - 2*pF;
%信息熵
Hp = -(pB.*log2(pB) + pC.*log2(pC) + pF.*log2(pF));
%求取最大熵
[max_Hp,max_pF] = max(Hp);
%绘图直观视图
plot(pF, Hp);
grid on;
set(gca,'XTickMode','manual','XTick',[0,pF(max_pF),0.325]);
set(gca,'YTickMode','manual','YTick',[0,max_Hp],Hp(end));

这里写图片描述

以上，我们根据未知的概率分布表示了约束条件，又用这些约束条件消去了两个变量，用剩下的变量表示熵，最后求出了熵最大时剩余变量的值，结果就求出了一个符合约束条件的概率分布，它有最大不确定性，我们在概率估计中没有引入任何偏差。

最大熵模型的一个经典的例子

坚持无偏原则

一篇文章中出现了“学习”这个词，那这个词是主语、谓语、还是宾语呢？换言之，已知“学习”可能是动词，也可能是名词，故“学习”可以被标为主语、谓语、宾语、定语等等。

令x1表示“学习”被标为名词， x2表示“学习”被标为动词。
令y1表示“学习”被标为主语， y2表示被标为谓语， y3表示宾语， y4表示定语。
$p (x 1) + p (x 2) = 1 \sum i = 1 4 p (y i) = 1$ 根据无偏原则，得到如下的推测：
$p (x 1 = p (x 2) = 0.5 p (y 1) = p (y 2) = p (y 3) = p (y 4) = 0.25$
进一步，若已经知道“学习”被标为定语的可能性很小，只有0.05，即 p(y4)=0.05 ，此时依然根据无偏原则得到：
$p (x 1 = p (x 2) = 0.5 p (y 1) = p (y 2) = p (y 3) = 0.95 3$
当“学习”被标作动词的时候，它被标作谓语的概率为0.95，即 p(y2|x1)=0.95 ，此时仍然按照需要坚持无偏见原则，使得概率分布尽量平均。但怎么样才能得到尽量无偏见的分布？事实上，概率平均分布等价于熵最大。于是，问题便转化为了：计算X和Y的分布，使得H(Y|X)达到最大值，并且满足下述条件：
$p (x 1) + p (x 2) = 1 \sum i = 1 4 p (y i) = 1 p (y 4) = 0.05 p (y 2 | x 1) = 0.95$
故要最大化下述式子：

且满足以下4个约束条件：
$p (x 1) + p (x 2) = 1 \sum i = 1 4 p (y i) = 1 p (y 4) = 0.05 p (y 2 | x 1) = 0.95$

最大熵模型的公式表示

至此，我们可以写出最大熵模型的一般表达式了，如下：
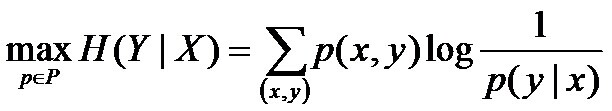
这里写图片描述
其中，P={p | p是X上满足条件的概率分布}
后面还有一系列的推导，最后由lagrange函数将原约束最优化问题转换为无约束的最优化的对偶问题。也就是《数学之美》中给出的最大熵模型。这里因为在我的学习中没有涉及到具体深入应用，不希望在这上面花费太多功夫，具体的推导过程可以参看博文《最大熵模型中的数学推导》。

参考文献
http://www.zhizhihu.com/html/y2011/3500.html
http://www.52nlp.cn/mit-nlp-fifth-lesson-maximum-entropy-and-log-linear-models-fifth-part
http://blog.csdn.net/lg1259156776/article/details/47271673
http://www.kuqin.com/shuoit/20141027/342889.html

posted @ 2017-10-28 15:10 落痕的寒假阅读(52) 评论(0) 编辑收藏举报

刷新页面返回顶部

落痕的寒假

今天也要加油鸭