[OpenCV实战]21 使用OpenCV的Eigenface
目录
在这篇文章中,我们将学习Eigenface(特征脸),主成分分析(PCA)在人脸中的应用。
1 PCA
美国人口约为3.25亿。你可能认为数百万人会有一百万种不同的想法,观点和想法,毕竟每个人都是独一无二的。对吗?错误!人类就像绵羊。我们跟着一群人。这很可悲但却是真实的。假设您在美国选择了20个最重要的政治问题,并要求数百万人使用“是”或“否”来回答这些问题。这里有一些例子:
- 你支持枪支控制吗?
- 你支持女人堕胎的权利吗
你有20个问题,每个问题必须使用是或否来回答,从技术上讲你可以获得2的20次方个不同的答案。实践中,您会注意到答案集要小得多。事实上,你用一个问题替换前20个问题“你是民主人士还是共和党人?”并准确地准确预测其余问题的答案。因此,这个20维数据被压缩到一个维度,没有太多信息丢失!
这正是PCA允许我们做的事情。在多维数据中,它将帮助我们找到最有用且包含最多信息的维度。它将帮助我们通过减少维度从数据中提取重要信息。我们需要一些数学工具来理解PCA,让我们从统计学中一个重要概方差开始。本文所有代码见:
https://github.com/luohenyueji/OpenCV-Practical-Exercise
1.1 方差是什么
方差衡量数据的分散程度。在下图图左中,这些点具有较高的方差,因为它们是十分分散的,但在下图图右中,这些点的方差很小,因为它们靠得很近。另请注意,在下图图左中,方差在所有方向上都不相同。最大方差的方向尤为重要。让我们看看为什么。

方差对数据中包含的信息进行编码。例如,如果您有由(X,Y)坐标点表示的2D数据。对于n个这样的点,您需要2n个数字来表示此数据。考虑一种特殊情况,其中对于每个数据点,沿y轴的值为0(或常数)。如下图所示。可以说y轴方向没有(或很少)信息。您可以使用n个数字来紧凑地表示此数据,以表示沿x轴的值,并且仅使用1个通用数字来表示沿y轴的常量。因为沿x轴有更大的方差,所以有更多的信息,因此我们必须使用更多的数字来表示这些数据。另一方面,由于沿y轴方差很小,因此可以使用单个数字来表示沿该轴的n个点中包含的所有信息。

1.2 什么是PCA
现在考虑使用红点在下图中显示的稍微复杂的数据集。数据以大致看起来像椭圆的形状分散。椭圆的主轴是最大方差的方向,正如我们现在所知,它是最大信息的方向。该方向下图中的蓝线表示,称为数据的第一个主要组成部分。
第二主成分是垂直于第一主成分方向的最大方差的方向。在2D中,只有一个方向垂直于第一个主成分,因此它是第二个主成分。使用绿线在下图中显示了这一点。

现在考虑下图所示分布像椭球一样的3D数据。第一个主成分用蓝线表示。有一个垂直于第一主成分的整个平面。第二主成分被选择为该平面中的最大方差的方向。您可能已经猜到,第三个主要成分只是垂直于第一个和第二个主成分的方向。
在这篇文章的开头,我们曾提到PCA的最大动机是减少维数。换句话说,我们希望使用更少的维度捕获数据中包含的信息。让我们考虑下图中所示的3D数据。每个数据点都有3个坐标 x,y和z,它们表示沿X,Y和Z轴的值。请注意,三个主要成分只是一组新的轴,因为它们彼此垂直。我们可以将这些主要分量称为X',Y'和Z'轴。

实际上,您可以将X,Y,Z轴与3D中的所有数据点一起旋转,使得X轴与第一主成分对齐,Y轴与第二主成分对齐,Z轴对齐第三个主要组成部分。通过应用该旋转,我们可以将XYZ坐标系中的任何点(x,y,z)变换为新X'Y'Z'坐标系中的点(x',y',z')。它是在不同坐标系中呈现的相同信息,但是这个新坐标系X'Y'Z'的美妙之处在于X'中包含的信息是最大的,接着是Y'然后是Z'。如果你为每个点(x',y',z')删除坐标z',我们仍然保留大部分信息,但现在我们只需要两个维度来表示这些数据。这可能看起来像一个小的改动,但如果您有1000维数据,您可以将维度显着减少到可能只有20个维度。除了减小尺寸外,PCA还将消除数据中的噪声。
1.3 什么是矩阵的特征向量和特征值?
在下一节中,我们将逐步解释如何计算PCA,但在我们这样做之前,我们需要了解特征向量和特征值是什么。考虑以下3×3矩阵:

考虑一个特殊的向量v,其中
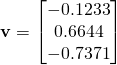
让我们将矩阵A与向量v相乘,看看为什么这个向量是特殊的。

所以其![]() 是标量(只是一个数字),称为对应于特征向量
是标量(只是一个数字),称为对应于特征向量![]() 的特征值。
的特征值。
1.4 如何计算PCA
通常,您可以使用您选择的线性代数包轻松找到给定数据的主要成分。在下一篇文章中,我们将学习如何在OpenCV中使用PCA类。在这里,我们简要介绍计算PCA的步骤,以便了解它在各种数学包中的实现方式。
以下是计算PCA的步骤。为简单起见,我们已经解释了使用3D数据的步骤,但同样的想法适用于任意数量的维度。
1)获得数据矩阵:第一步是将所有数据点组合成一个矩阵,其中每列是一个数据点。三维数据矩阵是这样的:

2)计算平均值:下一步是计算所有数据点的平均值(平均值)。注意,如果数据是3D,则平均值也是具有x,y和z坐标的3D点。类似地,如果数据是m维,则平均值也是m维。平均值![]() 的计算公式如下:
的计算公式如下:

3)从数据矩阵中减去均值:我们接下来通过从D中每个数据点减去平均值来创建另一个矩阵M:
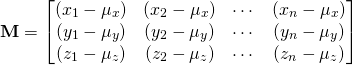
4)计算协方差矩阵:记住我们想要找到最大方差的方向。协方差矩阵捕获有关数据传播的信息。协方差矩阵的对角元素是沿X,Y和Z轴的方差。非对角线元素表示两个维度(X和Y,Y和Z,Z和X)之间的协方差。协方差矩阵C使用以下乘积计算。
![]()
其中,Ť代表转置操作。C的维度是3。图5示出了根据数据的不同方向协方差矩阵的变化如何。下图中:左图:当数据在所有方向上均匀分布时,协方差矩阵具有相等的对角线元素和零非对角线元素。中图:当数据传播沿其中一个轴伸长时,对角线元素不相等,但非对角线元素为零。右图:通常协方差矩阵具有对角线和非对角线元素。

5)计算协方差矩阵的特征向量和特征值:主成分是协方差矩阵的特征向量。第一主分量是对应于最大特征值的特征向量,第二主分量是对应于第二大特征值的特征向量,依此类推。
2 什么是EigenFaces?
特征脸是可以添加到平均人脸图像(训练集多张正面脸的均值图像)以创建新脸部图像的图像。我们可以用以下数学公式计算:
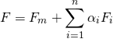
其中
F是一张新生成的脸部图像。
Fm是平均人脸图像,
Fi是一个EigenFace(特征脸),
![]() 是我们可以选择创建新图的标量系数,可正可负。
是我们可以选择创建新图的标量系数,可正可负。
通过估计面部图像的数据集的主要分量来计算特征脸。它们用于人脸识别和面部特征点检测等应用。
2.1 将图像作为向量
在上一篇文章中,显示的所有示例都是2D或3D数据点。我们了解到,如果我们收集了这些点,我们就可以找到主要成分。但是,我们如何将图像表示为更高维空间中的一个点?我们来看一个例子。
100 x 100彩色图像只是100 x 100 x 3(每个R,G,B颜色通道一个)的数组。通常,我们喜欢将100 x 100 x 3阵列视为3D阵列,但您可以将其视为由30,000个元素组成的长1D阵列。
您可以将这个30k个元素数组视为30k维空间中的一个点,就像您可以想象一个由3个数字(x,y,z)组成的数组作为3D空间中的一个点!
你如何想象30k维空间?你不能。大多数情况下,您可以将您的参数构建为好像只有三个维度,并且通常(但并非总是),它们也适用于更高维度的空间。
2.2 如何计算如何计算EigenFaces
要计算EigenFaces,我们需要使用以下步骤:
1)获取面部图像数据集:我们需要一组包含不同类型面部的面部图像。在这篇文章中,我们使用了来自CelebA的约200张图片。CelebA数据集见:
http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html
2)对齐和调整图像大小:接下来我们需要对齐和调整图像大小,以便在所有图像中眼睛的中心都是对齐的。这可以通过首先找到面部特征点来完成。在这篇文章中,我们使用了CelebA中提供的对齐图像。此时,数据集中的所有图像应该具有相同的大小。
3)创建数据矩阵:创建一个包含所有图像作为行向量的数据矩阵。如果数据集中的所有图像大小为100 x 100且有1000个图像,我们将拥有大小为30k x 1000的数据矩阵。
4)计算平均向量[可选]:在对数据执行PCA之前,我们需要减去平均向量。在我们的例子中,平均向量将是通过平均数据矩阵的所有行计算的30k×1行向量。使用OpenCV的PCA类不需要计算这个平均向量的原因是因为如果没有提供向量,OpenCV可以方便地计算我们的平均值。在其他线性代数包中可能不是这种情况。
5)计算主成分:通过找到协方差矩阵的特征向量来计算该数据矩阵的主成分。幸运的是,OpenCV中的PCA类为我们处理了这个计算。我们只需要提供数据矩阵,然后输出一个包含Eigenvectors的矩阵。
6)重塑特征向量以获得EigenFaces:如果我们的数据集包含大小为100 x 100 x 3的图像,那么如此获得的特征向量将具有30k的长度。我们可以将这些特征向量重塑为100 x 100 x 3图像以获得EigenFaces。
3 使用OpenCV进行主成分分析(PCA)
OpenCV中的PCA类允许我们计算数据矩阵的主要成分。这里我们讨论使用PCA类的最常用方法。不同用法见文档:
https://docs.opencv.org/4.1.0/d3/d8d/classcv_1_1PCA.html
C++接口代码如下:
PCA (Mat &data, Mat &mean, int flags, int maxComponents=0)
// Example usage
PCA pca(data, Mat(), PCA::DATA_ORDER_ROW, 10);
Mat mean = pca.mean;
Mat eigenVectors = pca.eigenvectorspython接口代码如下:
mean, eigenvectors = cv2.PCACompute ( data, mean=mean, maxComponents=maxComponents )
// Example usage
mean, eigenVectors = cv2.PCACompute(data, mean=None, maxComponents=10)各个参数介绍如下:
1)data:包含每个数据点的数据矩阵,作为行向量或列向量。如果我们的数据由1000个图像组成,并且每个图像是30k长的行向量,则数据矩阵将为30k×1000。
2)mean:数据的平均值。如果数据矩阵中的每个数据点都是30k长的行向量,则均值也将是相同大小的向量。此参数是可选的,如果未提供,则在内部计算。
3)flags:它可以取值DATA_AS_ROW或DATA_AS_COL,指示数据矩阵中的点是沿着行还是沿着列排列。在我们共享的代码中,我们将其安排为行向量。
4)maxComponents:确定主成分的个数。主成分的最大数量通常是两个值中较小的一个:原始数据的维度(在我们的例子中是30k)或数据点的数量(例如上例中的1000)。但是,我们可以通过设置此参数来明确确定我们想要计算的最大主成分数。例如,我们可能只对前50个主成分感兴趣。
所有代码如下:
C++:
#include "pch.h"
#include <iostream>
#include <fstream>
#include <sstream>
#include <opencv2/core/core.hpp>
#include "opencv2/imgcodecs.hpp"
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/opencv.hpp>
#include "dirent.h"
#include <stdlib.h>
#include <time.h>
using namespace cv;
using namespace std;
#define MAX_SLIDER_VALUE 255
//主成分个数
#define NUM_EIGEN_FACES 10
// Weights for the different eigenvectors
int sliderValues[NUM_EIGEN_FACES];
// Matrices for average (mean) and eigenvectors
Mat averageFace;
vector<Mat> eigenFaces;
// Read jpg files from the directory
void readImages(string dirName, vector<Mat> &images)
{
cout << "Reading images from " << dirName;
// Add slash to directory name if missing
if (!dirName.empty() && dirName.back() != '/')
{
dirName += '/';
}
DIR *dir;
struct dirent *ent;
int count = 0;
//image extensions 图像后缀
string imgExt = "jpg";
vector<string> files;
if ((dir = opendir(dirName.c_str())) != NULL)
{
/* print all the files and directories within directory */
while ((ent = readdir(dir)) != NULL)
{
if (strcmp(ent->d_name, ".") == 0 || strcmp(ent->d_name, "..") == 0)
{
continue;
}
string fname = ent->d_name;
if (fname.find(imgExt, (fname.length() - imgExt.length())) != std::string::npos)
{
string path = dirName + fname;
Mat img = imread(path);
if (!img.data)
{
cout << "image " << path << " not read properly" << endl;
}
else
{
// Convert images to floating point type 保存图像
img.convertTo(img, CV_32FC3, 1 / 255.0);
images.push_back(img);
// A vertically flipped image is also a valid face image.
// So lets use them as well. 翻转图像
Mat imgFlip;
flip(img, imgFlip, 1);
images.push_back(imgFlip);
}
}
}
closedir(dir);
}
// Exit program if no images are found
if (images.empty())
{
exit(EXIT_FAILURE);
}
cout << "... " << images.size() / 2 << " files read" << endl;
}
// Create data matrix from a vector of images 创建图像矩阵
static Mat createDataMatrix(const vector<Mat> &images)
{
cout << "Creating data matrix from images ...";
// Allocate space for all images in one data matrix.
// The size of the data matrix is
//
// ( w * h * 3, numImages )
//
// where,
//
// w = width of an image in the dataset.
// h = height of an image in the dataset.
// 3 is for the 3 color channels.
Mat data(static_cast<int>(images.size()), images[0].rows * images[0].cols * 3, CV_32F);
// Turn an image into one row vector in the data matrix
for (unsigned int i = 0; i < images.size(); i++)
{
// Extract image as one long vector of size w x h x 3 重新设置通道行数大小
//reshape函数第一个参数通道数,第二个参数行数,和python中reshape函数不一样。
Mat image = images[i].reshape(1, 1);
// Copy the long vector into one row of the destm
image.copyTo(data.row(i));
}
cout << " DONE" << endl;
return data;
}
// Calculate final image by adding weighted
// EigenFaces to the average face.
void createNewFace(int, void *)
{
// Start with the mean image
Mat output = averageFace.clone();
// Add the eigen faces with the weights
for (int i = 0; i < NUM_EIGEN_FACES; i++)
{
// OpenCV does not allow slider values to be negative.
// So we use weight = sliderValue - MAX_SLIDER_VALUE / 2
double weight = sliderValues[i] - MAX_SLIDER_VALUE / 2;
//获得输出图像
output = output + eigenFaces[i] * weight;
}
resize(output, output, Size(), 2, 2);
imshow("Result", output);
}
// Reset slider values
void resetSliderValues(int event, int x, int y, int flags, void* userdata)
{
if (event == EVENT_LBUTTONDOWN)
{
for (int i = 0; i < NUM_EIGEN_FACES; i++)
{
sliderValues[i] = 128;
setTrackbarPos("Weight" + to_string(i), "Trackbars", MAX_SLIDER_VALUE / 2);
}
createNewFace(0, 0);
}
}
int main()
{
// Directory containing images 用于获取平均图像目录
string dirName = "image/";
// Read images in the directory 从目录中读取图像
vector<Mat> images;
readImages(dirName, images);
// Size of images. All images should be the same size. 图像尺寸
Size sz = images[0].size();
// Create data matrix for PCA. 为PCA创建数据矩阵
Mat data = createDataMatrix(images);
// Calculate PCA of the data matrix 计算PCA
cout << "Calculating PCA ...";
//提取十个主成分
PCA pca(data, Mat(), PCA::DATA_AS_ROW, NUM_EIGEN_FACES);
cout << " DONE" << endl;
// Extract mean vector and reshape it to obtain average face 获得均值图
//reshape函数第一个参数通道数,第二个参数行数,和python中reshape函数不一样。
averageFace = pca.mean.reshape(3, sz.height);
// Find eigen vectors. 寻找eign向量
Mat eigenVectors = pca.eigenvectors;
// Reshape Eigenvectors to obtain EigenFaces 获得Eign图
for (int i = 0; i < NUM_EIGEN_FACES; i++)
{
Mat eigenFace = eigenVectors.row(i).reshape(3, sz.height);
eigenFaces.push_back(eigenFace);
}
// Show mean face image at 2x the original size
Mat output;
//图像长宽都变成原来的两倍
resize(averageFace, output, Size(), 2, 2);
namedWindow("Result", CV_WINDOW_AUTOSIZE);
imshow("Result", output);
// Create trackbars
namedWindow("Trackbars", CV_WINDOW_AUTOSIZE);
for (int i = 0; i < NUM_EIGEN_FACES; i++)
{
//滑动窗格
sliderValues[i] = MAX_SLIDER_VALUE / 2;
createTrackbar("Weight" + to_string(i), "Trackbars", &sliderValues[i], MAX_SLIDER_VALUE, createNewFace);
}
// You can reset the sliders by clicking on the mean image.
setMouseCallback("Result", resetSliderValues);
cout << "Usage:" << endl
<< "\tChange the weights using the sliders" << endl
<< "\tClick on the result window to reset sliders" << endl
<< "\tHit ESC to terminate program." << endl;
waitKey(0);
destroyAllWindows();
return 0;
}python:
# Import necessary packages
from __future__ import print_function
import os
import sys
import cv2
import numpy as np
# Create data matrix from a list of images
def createDataMatrix(images):
print("Creating data matrix",end=" ... ")
'''
Allocate space for all images in one data matrix.
The size of the data matrix is
( w * h * 3, numImages )
where,
w = width of an image in the dataset.
h = height of an image in the dataset.
3 is for the 3 color channels.
'''
numImages = len(images)
sz = images[0].shape
data = np.zeros((numImages, sz[0] * sz[1] * sz[2]), dtype=np.float32)
for i in range(0, numImages):
image = images[i].flatten()
data[i,:] = image
print("DONE")
return data
# Read images from the directory
def readImages(path):
print("Reading images from " + path, end="...")
# Create array of array of images.
images = []
# List all files in the directory and read points from text files one by one
for filePath in sorted(os.listdir(path)):
fileExt = os.path.splitext(filePath)[1]
if fileExt in [".jpg", ".jpeg"]:
# Add to array of images
imagePath = os.path.join(path, filePath)
im = cv2.imread(imagePath)
if im is None :
print("image:{} not read properly".format(imagePath))
else :
# Convert image to floating point
im = np.float32(im)/255.0
# Add image to list
images.append(im)
# Flip image
imFlip = cv2.flip(im, 1);
# Append flipped image
images.append(imFlip)
numImages = int(len(images) / 2)
# Exit if no image found
if numImages == 0 :
print("No images found")
sys.exit(0)
print(str(numImages) + " files read.")
return images
# Add the weighted eigen faces to the mean face
def createNewFace(*args):
# Start with the mean image
output = averageFace
# Add the eigen faces with the weights
for i in range(0, NUM_EIGEN_FACES):
'''
OpenCV does not allow slider values to be negative.
So we use weight = sliderValue - MAX_SLIDER_VALUE / 2
'''
sliderValues[i] = cv2.getTrackbarPos("Weight" + str(i), "Trackbars");
weight = sliderValues[i] - MAX_SLIDER_VALUE/2
output = np.add(output, eigenFaces[i] * weight)
# Display Result at 2x size
output = cv2.resize(output, (0,0), fx=2, fy=2)
cv2.imshow("Result", output)
def resetSliderValues(*args):
for i in range(0, NUM_EIGEN_FACES):
cv2.setTrackbarPos("Weight" + str(i), "Trackbars", int(MAX_SLIDER_VALUE/2));
createNewFace()
if __name__ == '__main__':
# Number of EigenFaces
NUM_EIGEN_FACES = 10
# Maximum weight
MAX_SLIDER_VALUE = 255
# Directory containing images
dirName = "image"
# Read images
images = readImages(dirName)
# Size of images
sz = images[0].shape
# Create data matrix for PCA.
data = createDataMatrix(images)
# Compute the eigenvectors from the stack of images created
print("Calculating PCA ", end="...")
mean, eigenVectors = cv2.PCACompute(data, mean=None, maxComponents=NUM_EIGEN_FACES)
print ("DONE")
averageFace = mean.reshape(sz)
eigenFaces = [];
for eigenVector in eigenVectors:
eigenFace = eigenVector.reshape(sz)
eigenFaces.append(eigenFace)
# Create window for displaying Mean Face
cv2.namedWindow("Result", cv2.WINDOW_AUTOSIZE)
# Display result at 2x size
output = cv2.resize(averageFace, (0,0), fx=2, fy=2)
cv2.imshow("Result", output)
# Create Window for trackbars
cv2.namedWindow("Trackbars", cv2.WINDOW_AUTOSIZE)
sliderValues = []
# Create Trackbars
for i in range(0, NUM_EIGEN_FACES):
sliderValues.append(int(MAX_SLIDER_VALUE/2))
cv2.createTrackbar( "Weight" + str(i), "Trackbars", int(MAX_SLIDER_VALUE/2), MAX_SLIDER_VALUE, createNewFace)
# You can reset the sliders by clicking on the mean image.
cv2.setMouseCallback("Result", resetSliderValues);
print('''Usage:
Change the weights using the sliders
Click on the result window to reset sliders
Hit ESC to terminate program.''')
cv2.waitKey(0)
cv2.destroyAllWindows()
上面的代码执行以下操作。
1)将特征脸的数量(NUM_EIGEN_FACES)设置为10,将滑块的最大值(MAX_SLIDER_VALUE)设置为255.这些数字不是一成不变的。更改这些数字以查看应用程序的更改方式。
读取图像:接下来,我们使用函数readImages读取指定目录中的所有图像。该目录包含已2)对齐的图像。所有图像中左眼和右眼的中心是相同的。我们将这些图像添加到列表(或矢量)中。我们还垂直翻转图像并将它们添加到列表中。因为并获取面部图像的镜像,我们3)创建图像数据矩阵。我们使用createDataMatrix函数将图像组合成数据矩阵。数据矩阵的每一行是一个图像。
4)计算PCA:接下来我们使用C ++中的PCA类和Python中的PCACompute函数计算PCA。作为PCA的输出,我们获得平均向量和10个特征向量。
5)重新设定图像维度以获得平均图像和特征图像:平均矢量和每个特征向量是长度为w * h * 3的向量,其中w是宽度,h是高度,3是数据集中任何图像的颜色通道数。换句话说,它们是30k元素的向量。我们将它们重新塑造为图像的原始大小,以获得平均面部图像和EigenFaces。
6)调整权重获得不同的图像。在OpenCV中,滑块值不能为负数。所以我们通过从当前滑块值中减去MAX_SLIDER_VALUE / 2来计算权重,这样我们就可以得到正值和负值。
结果如下图所示,左边是平均图像。在右边是一个新面孔,通过添加10个不同权重的特征面产生。在本文C++代码要添加一个dirent.h文件,自带代码就不列出来了,由于图像太少所以结果很模糊,加图像就行。不过opencv里面的pca计算很慢。

4 参考
https://www.learnopencv.com/eigenface-using-opencv-c-python/
本文来自博客园,作者:落痕的寒假,转载请注明原文链接:https://www.cnblogs.com/luohenyueji/p/16970318.html





