[OpenCV实战]49 对极几何与立体视觉初探

本文主要介绍对极几何(Epipolar Geometry)与立体视觉(Stereo Vision)的相关知识。对极几何简单点来说，其目的就是描述是两幅视图之间的内部对应关系，用来对立体视觉进行建模，实际上就是一种约束条件，这样可以确定立体匹配时的最优解。对极几何是计算机视觉领域中一个基础概念，具体可以学习文章-对极几何(Epipolar)。对极几何/极几何在各个坐标系（世界坐标系，观察坐标系，像素坐标系）相互转换中是十分重要的一个概念。立体视觉是一种很常用的计算机视觉技术，其目的是从两幅或两幅以上的图像中推理出图像中每个像素点的深度信息,这样可以重构出物体的三维信息，应用价值极高。具体介绍可以见立体视觉小结(重点基于双目视觉)和立体视觉（一概述）。

本文主要参考Introduction to Epipolar Geometry and Stereo Vision。
本文所有代码见：

github: OpenCV-Practical-Exercise
gitee(备份，主要是下载速度快): OpenCV-Practical-Exercise-gitee

值得注意的是，本文只是基础理论介绍，可以不看，实际这套理论工程并不多,代码也是半成品，了解下就行了。

1 基本理论

1.1 背景介绍

您是否曾经想过为什么戴着3D眼镜观看电影时能体验到如此奇妙的3D效果？或为什么一只眼睛闭上很难接乒乓球？所有这些都与立体视觉有关，立体视觉是我们用两只眼睛感知深度的能力。如下图所示，你可以看到人和椅子的相对移动距离。这篇文章就是使用OpenCV和立体视觉为计算机提供了这种感知深度的能力。该代码在Python和C++中提供。

在这里插入图片描述

当然要注意的是本文介绍的相关知识都是最基础的，实际上真实应用都是用深度学习来做以上工作，如下图我们常见的自动驾驶就搭载了基于深度学习的深度预测算法，图(b)中越黑的区域代表距离越远。具体可以见gluoncv-Depth Prediction。但是了解基础的立体视觉知识还是很有用的。

回到第一张所示人体和椅子的图，这张图除了能够检测出不同的对象外，计算机还能够分辨它们的距离。这意味着它可以感知深度！对于这张图，使用了OAK-D(OpenCV AI Kit-Depth)的立体摄像机来帮助计算机感知深度。那么什么是立体摄像机，我们如何使用它为计算机提供深度感？它与立体视觉有关吗？通过理解过与对极几何和立体视觉有关的基本概念可以回答这些问题。
想要学习立体视觉的基础知识，可以参考Multiple View Geometry in Computer Vision这本书。书出版时间挺久了，但是想要深入从事立体视觉相关的工作，这本书是必读的，里面有很多系统性的数学推导和理论解释，基本概念都有涉及。但是如果真的看不懂，用深度学习做做相关应用也是可以的。

1.2 为什么需要一张以上的图像来计算深度？

当我们捕获图像中的3D对象时，一般来说我们会将其从三维立体空间投影到二维平面投影空间。也就是我们所说的平面投影。问题是由于这种平面投影，我们会丢失物体深度信息。所以我们需要从二维平面图像恢复物体的深度三维信息。那么我们可以只从一张二维平面图像完成这项工作吗，具体看下面解答。

在下图中，C1和X是三维空间中的点，单位向量L1给出了光线从C1到X的方向。现在，如果我们知道点C1和方向向量L1的值，我们能找到X吗？

从几何数学上讲，它只意味着求解方程中的X:

$X = C 1 + K (L 1)$

但是现在，由于我们无法确定K的值，所以我们找不到X的唯一值。

那么在下图中，我们添加一个附加点C2和一个从C2到X的方向向量L2。如果我们也知道C2和L2，那么我们可以找到X的唯一值吗？答案是肯定的，因为从C1和C2发出的光线在一个唯一的点，即X点本身，清楚地相交。这种方法叫做三角测量/三角测量（Triangulation）。

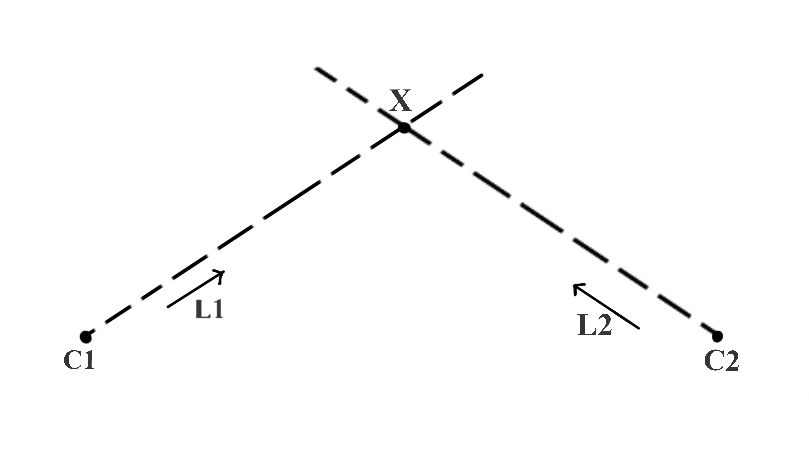
总之，如下图5所示，当在两个不同的视图（图像）中捕获（投影）时，如何使用三角测量来计算点（X）的深度。在该图中，C1和C2分别是左照相机和右照相机的已知3D位置。我们还需要知道L1和L2的相关系，因此通过照相机分别捕获X点的信息，得到图像x1和x2。x1是由左照相机捕获的3D点X的图像，x2是由右照相机捕获的X的图像。x1和x2被称为对应点，因为它们是同一个3D点的投影。我们用x1和C1来寻找L1，用x2和C2来寻找L2。这样我们获得求出X点的信息。

从上面的示例中，我们了解到要使用从不同视角捕获的两个图像对3D点进行三角测量，关键要求是：

摄像头的位置–C1和C2。
对应点的位置–x1和x2。

但这只是我们试图计算的一个点，根据不共线的三点可以确定一个平面。我们对两个视图中捕获的所有点重复上述过程，就可以捕捉真实世界场景来计算其中物体的三维结构。

1.3 对二视图几何的实践与理论理解

下图显示了两个从不同视角捕获现实场景的图像。为了计算3D结构，我们尝试找到前面提到的两个关键要求：摄像机在现实世界坐标系（C1和C2）中的位置。我们通过假设其中一个摄像机位置（C1或C2）作为原点来计算3D点来简化这个问题。我们通过使用已知的校准模式校准双视图系统来找到它。这个过程称为立体校准/立体定标。具体可以参考基于OpenCV的立体相机标定StereoCalibration与目标三维坐标定位。其次要计算的场景中每个3D点（X）的点对应关系（x1和x2）。我们将讨论计算点对应的各种改进，并最终了解对极几何如何帮助我们简化问题。

请注意，立体相机校准仅当图像由一对相互固定的相机捕获时才有用。如果一台相机从两个不同的角度拍摄图像，那么我们只能找到一个比例的深度。绝对深度是未知的，除非我们有一些关于捕获场景的特殊几何信息，可以用来找到实际的比例。

下图显示了手动标记的这些对应点。对我们来说，识别相应的点很容易，但是如何使计算机做到这一点呢。

人们在计算机视觉社区中经常使用的一种方法称为特征匹配。下图显示了使用ORB特征描述符在左右图像之间匹配的特征。这是一种找到点对应关系（匹配）的方法。

特征匹配应用很广泛，具体应用可以见[OpenCV实战]6 基于特征点匹配的视频稳像和[OpenCV实战]10 使用Hu矩进行形状匹配。

但是，我们观察到具有已知点对应关系的像素数与像素总数的比率是最小的。这意味着我们将拥有一个非常稀疏的3D场景。对于更密集的重建，我们需要获得尽可能多的像素点对应。找到点对应的一种简化方法是找到具有相似相邻像素信息的像素。在下图中，我们观察到使用这种匹配具有相似相邻信息的像素的方法会导致来自一个图像的单个像素在另一个图像中具有多个匹配。我们发现编写一个算法来确定真正的匹配很有挑战性，这就是为什么传统算法做立体视觉效果一般的一个主要原因。

有没有办法减少我们的搜索空间？我们可以使用一些定理来消除所有导致不正确对应的额外假匹配吗？我们在这里利用对极几何，下面我们将了解对极几何在减少点对应关系的搜索空间中的重要性。

1.4 对极几何及其在点对应中的应用

在下图中，分别通过C1和C2处的相机在x1和x2处捕获3D点X。因为x1是X的投影，所以如果我们尝试从C1穿过x1的光线R1延伸，它也应该穿过X。在图像i2中，此光线R1被捕获为线L2’，而X被捕获为x2。当X位于R1上时，x2应该位于L2’上。这样，x2的可能位置被限制在一条直线L22上。我们可以使用对极几何找到L2。

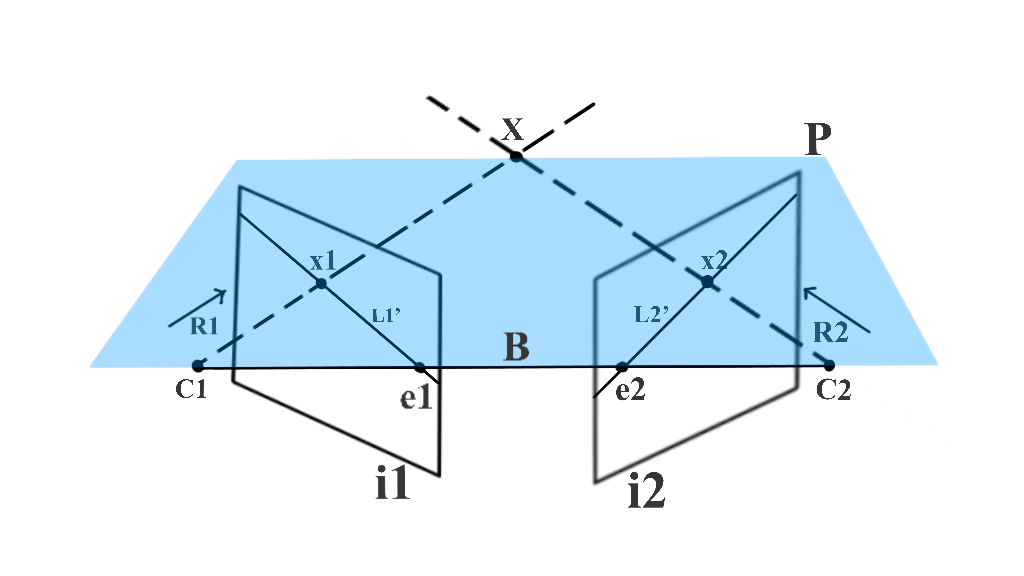
上图中e2是相机成像中心C1在图像i2中的投影，而e1是相机成像中心C2在图像i1中的投影。e1和e2 的术语是极点（epipole）。因此，在双视图几何设置中，极点是一个视图在另一个视图中的相机中心的图像。连接两个相机中心的线称为基线。因此，极点也可以定义为基线与图像平面的交点。上图中使用R1和基线，我们可以定义一个平面P。这个平面还包含X、C1、x1、x2和C2。我们称这个平面为极平面(Epipolar Plane)。此外，从极平面和图像平面的交点获得的线被称为极线（Epipolar geometry）。因此在我们的例子中，L2是一条极线（极平面P和图像i2的交点）。对于不同的X值，我们将有不同的极平面，因此不同的极线。然而，所有的极平面相交于基线，所有的极线相交于极点。所有这些一起形成了对极几何。

上面已经囊括了我们到目前为止所学到的所有技术术语。我们使用基线B和射线R1创建了极平面P。e1和e2是极点，L2是对极线。基于给定图的对极几何，将图像i2中与像素x1对应的像素的搜索空间限制为一条2D线，即极线l2。这称为极线约束。有没有办法用单个矩阵表示整个对极几何？此外，我们可以仅使用两个捕获的图像来计算该矩阵吗？好消息是有这样一个矩阵，它被称为基本矩阵（the Fundamental matrix。关于以上更详细的理论解释和公式推导见对极几何与基本矩阵和计算机视觉–对极几何与基础矩阵。这些东西不是几句话能讲清楚，如果专门研究这些东西，还是看Multiple View Geometry in Computer Vision这本书。

如果工程应用只要知道我们能够使用基本矩阵找到极线，通过OpenCV的findFundamentalMat方法提供了各种算法（例如7点算法，8点算法，RANSAC算法和LMedS算法）的实现，以使用匹配的特征点计算基本矩阵。

2 特例

现在我们来说说两视图视觉的特例-平行成像平面(parallel imaging planes)。我们一直在努力解决通信问题。我们开始使用特征匹配，但我们观察到它会导致一个稀疏的三维结构。我们学习了如何使用极线几何将点对应的搜索空间缩小到一条线——极线。那么我们可以进一步简化寻找密集点对应关系的过程吗？下图展示了显示特征匹配结果的图像和极线上的对应点结果的图像。不管是图(a)和图(b)显示了两对不同图像的特征匹配结果和极线约束。在特征匹配和极线方面，两个图形之间最显着的区别是什么？对于每张图的下图。我们会发现所有的极线平行，右图与左图中的各个点具有相同的纵坐标。我们在左图像的每个像素中搜索右图像的同一行中的相应像素。这是成像平面平行的两视图几何的特殊情况。这大大简化了密集点对应的问题。它帮助我们应用立体视差(stereo disparity)。它类似于立体视觉，帮助人类感知深度的方法。让我们详细了解一下。

下图是使用Middlebury Stereo Datasets 2005中的图像生成的。它演示了相机的纯平移运动，使成像平面平行。我们可以清楚地说，底部的玩具牛比最上面一排的玩具更接近镜头。我们是怎么做到的？我们基本上可以在两张图片中看到物体的移动。物体移动越少，物体离我们越近。这种转变就是我们所说的视差。

我们为每个像素计算视差（两个图像中像素的偏移），并应用比例映射来查找给定视差值的深度。Depth Map from Stereo Images中的图进一步证明了这一点。

上图解释了视差（x–x’）与深度Z之间的关系。视差= x – x’= Bf / Z。其中B是基线（相机之间的距离），f是焦距。上面公式具体推导见双目视觉的基础知识。

接下来使用OpenCV的StereoSGBM方法编写代码，以计算给定图像对的视差图。函数参数很多，具体介绍见StereoSGBM接口介绍，尽可能使用默认参数，如果自行设定参数注意查看详细函数说明，避免出错。

代码如下：

C++

#include <opencv2/opencv.hpp>
#include <stdio.h>
#include <string.h>

int main()
{
	cv::Mat imgL, imgR;

	// 读图
	imgL = cv::imread("images/im0.png", 0);
	cv::resize(imgL, imgL, cv::Size(600, 600));
	imgR = cv::imread("images/im1.png", 0);
	cv::resize(imgR, imgR, cv::Size(600, 600));

	int minDisparity = 0;
	int numDisparities = 64;
	int blockSize = 8;
	int disp12MaxDiff = 1;
	int uniquenessRatio = 10;
	int speckleWindowSize = 10;
	int speckleRange = 8;

	// 创建StereoSGBM对象
	cv::Ptr<cv::StereoSGBM> stereo = cv::StereoSGBM::create(minDisparity, numDisparities, blockSize, disp12MaxDiff, uniquenessRatio, speckleWindowSize, speckleRange);

	cv::Mat disp;
	// 计算视差
	stereo->compute(imgL, imgR, disp);

	// 结果归一化
	cv::normalize(disp, disp, 0, 255, cv::NORM_MINMAX, CV_8UC1);

	cv::imshow("Left image", imgL);
	cv::imshow("Right image", imgR);
	cv::imshow("disparity", disp);
	cv::waitKey(0);

	return 0;
}

Python

from __future__ import print_function

import numpy as np
import cv2


# ----- 读图
imgL = cv2.imread("images/im0.png",1)
imgL = cv2.resize(imgL,(600,600))

imgR = cv2.imread("images/im1.png",1)
imgR = cv2.resize(imgR,(600,600))

# Setting parameters for StereoSGBM algorithm
# 设置 StereoSGBM相关参数
minDisparity = 0
numDisparities = 64
blockSize = 8
disp12MaxDiff = 1
uniquenessRatio = 10
speckleWindowSize = 10
speckleRange = 8

# Creating an object of StereoSGBM algorithm
# 创建StereoSGBM对象
stereo = cv2.StereoSGBM_create(minDisparity = minDisparity,
    numDisparities = numDisparities,
    blockSize = blockSize,
    disp12MaxDiff = disp12MaxDiff,
    uniquenessRatio = uniquenessRatio,
    speckleWindowSize = speckleWindowSize,
    speckleRange = speckleRange
)

# Calculating disparith using the StereoSGBM algorithm
# 计算视差
disp = stereo.compute(imgL, imgR).astype(np.float32)

# 结果归一化
disp = cv2.normalize(disp,0,255,cv2.NORM_MINMAX)

# Displaying the disparity map
# 显示结果
cv2.imshow("disparity",disp)
cv2.imshow("left image",imgL)
cv2.imshow("right image",imgR)
cv2.waitKey(0)

cv2.destroyAllWindows()

上面程序结果如下图所示。

3 参考

3.1 理论

3.2 工程

posted @ 2021-02-12 16:27 落痕的寒假阅读(205) 评论(0) 编辑收藏举报

刷新页面返回顶部

落痕的寒假

今天也要加油鸭