[OpenCV实战]51 基于OpenCV实现图像极坐标变换与逆变换
在图像处理领域中,经常通过极坐标与笛卡尔直角坐标的互转来实现图像中圆形转为方形,或者通过极坐标反变换实现方形转圆形。例如钟表的表盘,人眼虹膜,医学血管断层都需要用到极坐标变换来实现圆转方。
文章目录
本文所有代码见:
- github: OpenCV-Practical-Exercise
- gitee(备份,主要是下载速度快): OpenCV-Practical-Exercise-gitee
1 基础数学知识
这一部分是高中数学知识,可以不看。
1.1 极坐标
关于极坐标的详细介绍见极坐标基本概念。在平面上,取一点O称为极点,从O出发的水平射线OX称为极轴,然后我们就可以确定了一个极坐标系。简单来说极坐标就是通过长度和角度来表示点的位置的坐标系。这个长度一般用 ρ \rho ρ表示,角度一般用 θ \theta θ表示(都是希腊字母,有些地方长度会用r来表示)。在程序语言中长度用变量rho来表示,角度用变量theta来表示(也就是它们的读音)。在极坐标系中任何一点的坐标都可以用 ( ρ , θ ) (\rho,\theta) (ρ,θ)来表示。如下图所示我们将极坐标和直角坐标叠在一起,根据三角相关公式,就能够得到相应的极坐标转换为直角坐标的公式。

详细的转换公式如下所示,其中 θ ∈ [ 0 , 2 π ] \theta \in [0,2\pi ] θ∈[0,2π]。
{ x = ρ cos ( θ ) y = ρ sin ( θ ) \left\{ \begin{array}{l} x = \rho \cos (\theta )\\ y = \rho \sin (\theta ) \end{array} \right. {x=ρcos(θ)y=ρsin(θ)
极坐标转为直角坐标的公式逆变换,就能够得到直角坐标转为极坐标的变换公式,如下所示。
{ ρ = x 2 + y 2 θ = arctan y x \left\{ \begin{array}{l} \rho = \sqrt {{x^2} + {y^2}} \\ \theta = \arctan \frac{y}{x} \end{array} \right. {ρ=x2+y2θ=arctanxy
1.2 二维直角坐标系转换
如下图所示。在坐标系XY上有任一一点P,该点的坐标为(x,y)。如果我们将坐标系XY逆时针旋转A度(逆时针为正)得到坐标系X’Y’,P点在坐标系X’Y’中的坐标为(x’,y’),在坐标系X’Y’中P点与X’轴角度为B度。那么(x,y)与(x’,y’)的转换关系是什么?

转换关系求解也很简单,见直角坐标系转换公式。简单来说,由上节知识我们知道在X’Y’坐标系中P点的坐标如下。
{ x ′ = ρ cos ( B ) y ′ = ρ sin ( B ) \left\{ \begin{array}{l} x' = \rho \cos (B)\\ y' = \rho \sin (B) \end{array} \right. {x′=ρcos(B)y′=ρsin(B)
P点在XY坐标系的坐标如下:
{
x
=
ρ
cos
(
A
+
B
)
=
ρ
cos
A
cos
B
−
ρ
sin
A
sin
B
y
=
ρ
sin
(
A
+
B
)
=
ρ
sin
A
cos
B
+
ρ
cos
A
sin
B
\left\{ \begin{array}{l} x = \rho \cos (A + B) = \rho \cos A\cos B - \rho \sin A\sin B\\ y = \rho \sin (A + B) = \rho \sin A\cos B + \rho \cos A\sin B \end{array} \right.
{x=ρcos(A+B)=ρcosAcosB−ρsinAsinBy=ρsin(A+B)=ρsinAcosB+ρcosAsinB
合并以上两个公式,就可以得到(x,y)与(x’,y’)的转换公式了。如下所示:
{ x = ρ cos ( A + B ) = x ′ cos A − y ′ sin A y = ρ sin ( A + B ) = x ′ sin A + y ′ cos A \left\{ \begin{array}{l} x = \rho \cos (A + B) = x'\cos A - y'\sin A\\ y = \rho \sin (A + B) = x'\sin A + y'\cos A \end{array} \right. {x=ρcos(A+B)=x′cosA−y′sinAy=ρsin(A+B)=x′sinA+y′cosA
2 圆形区域转换为矩形区域
2.1 预设值
我们想要将图像中圆环区域展开成矩形长条可以通过第一章的极坐标变换知识来实现。如下图所示是常见的钟表图像。

我们对这种圆盘或者圆环类的区域很难处理,所以需要转为矩形长条,实现这一步骤需要预先设定一系列的值:
- 将圆盘区域从图像中提取出来,并统一设置图像尺寸为预先给定的固定大小(通常是正方形)。
- 根据预先给定的固定大小设置圆盘区域的半径和圆心坐标。半径一般是圆盘图像高的一半,圆心通常是圆盘图像的中心点。
- 设置转换后矩形长条图像摆放方向,矩形长条摆放圆形区域可以是从上到下或者从左至右,本文选择从左至右。
- 设置矩形长条图像的尺寸,矩形图像的宽通常是圆形区域的周长。高通常自己按实际任务给定,要么是图像中圆环区域的宽度,或者是圆形区域的半径的一半。
经过以上设定,我们要输入进行转换的圆形区域图像如下图所示。这张图像来自github开源代码cv-warpPolar-example。关于极坐标变换的相关学习也可以见该开源代码仓库。其他一些可以学习的文章见:将图像中圆环区域展开成矩形长条的方法和二维向量旋转公式。

我们预设值的全局变量代码如下。
C++
// ----- 全局参数
// PAI值
double PI = M_PI;
// 设置输入图像固定尺寸(必要)
double HEIGHT = 300;
double WIDTH = 300;
// 输入图像圆的半径,一般是宽高一半
int CIRCLE_RADIUS = int(HEIGHT / 2);
// 圆心坐标
cv::Point CIRCLE_CENTER = cv::Point(int(WIDTH / 2), int(HEIGHT / 2));
// 极坐标转换后图像的高,可自己设置
int LINE_HEIGHT = int(CIRCLE_RADIUS / 1.5);
// 极坐标转换后图像的宽,一般是原来圆形的周长
int LINE_WIDTH = int(2 * CIRCLE_RADIUS * PI);
// C++ OpenCV Mat读像素值用
typedef Point3_<uint8_t> Pixel;
Python
# ----- 全局参数
# PAI值
PI = math.pi
# 设置输入图像固定尺寸(必要)
HEIGHT, WIDTH = 300, 300
# 输入图像圆的半径,一般是宽高一半
CIRCLE_RADIUS = int(HEIGHT / 2)
# 圆心坐标
CIRCLE_CENTER = [HEIGHT / 2, WIDTH / 2]
# 极坐标转换后图像的高,可自己设置
LINE_HEIGHT = int(CIRCLE_RADIUS / 1.5)
# 极坐标转换后图像的宽,一般是原来圆形的周长
LINE_WIDTH = int(2 * CIRCLE_RADIUS * PI)
2.2 标准圆形转换
所以标准圆形转换,就是上图表针我们从3点钟开始,逆时针将圆形图像展开。具体步骤如下图所示。

详细来说分为三步:
2.2.1 Step1 获得各点的极坐标
首先我们获得圆形区域各个点的极坐标。对于圆形各点的角度,我们从3点钟开始,逆时针旋转计算角度值,对于圆形的半径,先计算外圈半径,然后计算逐渐往内计算内圈半径。其中极坐标系中的极轴为3点钟方向对应的轴。这一部分计算代码如下:
C++
// 最后的-0.2是用于优化结果,可以自行调整
theta = PI * 2 / LINE_WIDTH * (col + 1) - 0.2;
rho = CIRCLE_RADIUS - row - 1;
Python
# 角度,最后的-0.2是用于优化结果,可以自行调整
theta = PI * 2 / LINE_WIDTH * (col + 1) - 0.2
# 半径,减1防止超界
rho = CIRCLE_RADIUS - row - 1
注意,这个转换的效果不同项目不一样,所以在角度半径后加一个优化值,实际自行调整该值(图像处理过度依赖设计者的经验)。
2.2.2 Step2 获得直角坐标
这里的直角坐标系是指以(0,0)点为原点。从原点出发的水平轴为x轴,x轴往右为正向;从原点出发的垂直轴为y轴,y轴往上为正向。这样应用第一节的极坐标转换公式就能获得圆形各个点的直角坐标。
2.2.3 Step3 获得OpenCV图像坐标
OpenCV的图像坐标系和普通的直接坐标系区别就是,OpenCV的图像坐标系中以y轴往下为正向。所以上一步获得的直角坐标中y值要乘上-1。然后我们要将圆形展开为矩形,需要将坐标原点移到圆形中点,这样就是x,y坐标各加上圆形中点的值。代码如下:
C++
int x = int(CIRCLE_CENTER.x + rho * std::cos(theta) + 0);
int y = int(CIRCLE_CENTER.y - rho * std::sin(theta) + 0);
Python
x = int(CIRCLE_CENTER[0] + rho * math.cos(theta) + 0.0)
y = int(CIRCLE_CENTER[1] - rho * math.sin(theta) + 0.0)
2.2.4 示例代码
上一步中,我们对圆形区域图像的每个点进行转换操作,再赋值给展开后的矩形图像就行了。代码如下:
C++
#include <opencv2/opencv.hpp>
#define _USE_MATH_DEFINES
#include <math.h>
#include <iostream>
using namespace std;
using namespace cv;
// ----- 全局参数
// PAI值
double PI = M_PI;
// 设置输入图像固定尺寸(必要)
double HEIGHT = 300;
double WIDTH = 300;
// 输入图像圆的半径,一般是宽高一半
int CIRCLE_RADIUS = int(HEIGHT / 2);
// 圆心坐标
cv::Point CIRCLE_CENTER = cv::Point(int(WIDTH / 2), int(HEIGHT / 2));
// 极坐标转换后图像的高,可自己设置
int LINE_HEIGHT = int(CIRCLE_RADIUS / 1.5);
// 极坐标转换后图像的宽,一般是原来圆形的周长
int LINE_WIDTH = int(2 * CIRCLE_RADIUS * PI);
// Define a pixel
typedef Point3_<uint8_t> Pixel;
cv::Mat create_line_image(cv::Mat img)
{
cv::Mat line_image = cv::Mat::zeros(Size(LINE_WIDTH, LINE_HEIGHT), CV_8UC3);
// 角度
double theta;
// 半径
double rho;
// 按照圆的极坐标赋值
for (int row = 0; row < line_image.rows; row++)
{
for (int col = 0; col < line_image.cols; col++)
{
// 最后的-0.1是用于优化结果,可以自行调整
theta = PI * 2 / LINE_WIDTH * (col + 1) - 0.2;
rho = CIRCLE_RADIUS - row - 1;
int x = int(CIRCLE_CENTER.x + rho * std::cos(theta) + 0);
int y = int(CIRCLE_CENTER.y - rho * std::sin(theta) + 0);
// Obtain pixel at(y,x)直接访问像素数据(效率不高,可以修改)
Pixel pixel = img.at<Pixel>(y, x);
// 赋值
line_image.at<Pixel>(row, col) = pixel;
}
}
// 如果想改变输出图像方向,旋转就行了
// cv::rotate(line_image, line_image, cv::ROTATE_90_CLOCKWISE);
return line_image;
}
// ----- 主程序
int main()
{
// 输入图像路径
String imgpath = "./image/clock.jpg";
// 读取图像
cv::Mat img = cv::imread(imgpath);
if (img.empty())
{
printf("please check image path");
return -1;
}
// 图像重置为固定大小
cv::resize(img, img, Size(WIDTH, HEIGHT));
printf("shape is: %d,%d", img.rows, img.cols);
// 展示原图
cv::imshow("src", img);
cv::Mat output = create_line_image(img);
// 展示结果
cv::imshow("dst", output);
cv::waitKey();
cv::destroyAllWindows();
system("pause");
return 0;
}
Python
import numpy as np
import math
import cv2
# ----- 全局参数
# PAI值
PI = math.pi
# 设置输入图像固定尺寸(必要)
HEIGHT, WIDTH = 300, 300
# 输入图像圆的半径,一般是宽高一半
CIRCLE_RADIUS = int(HEIGHT / 2)
# 圆心坐标
CIRCLE_CENTER = [HEIGHT / 2, WIDTH / 2]
# 极坐标转换后图像的高,可自己设置
LINE_HEIGHT = int(CIRCLE_RADIUS / 1.5)
# 极坐标转换后图像的宽,一般是原来圆形的周长
LINE_WIDTH = int(2 * CIRCLE_RADIUS * PI)
# ----- 将圆环变为矩形
def create_line_image(img):
# 建立展开后的图像
line_image = np.zeros((LINE_HEIGHT, LINE_WIDTH, 3), dtype=np.uint8)
# 按照圆的极坐标赋值
for row in range(line_image.shape[0]):
for col in range(line_image.shape[1]):
# 角度,最后的-0.1是用于优化结果,可以自行调整
theta = PI * 2 / LINE_WIDTH * (col + 1) - 0.2
# 半径,减1防止超界
rho = CIRCLE_RADIUS - row - 1
x = int(CIRCLE_CENTER[0] + rho * math.cos(theta) + 0.0)
y = int(CIRCLE_CENTER[1] - rho * math.sin(theta) + 0.0)
# 赋值
line_image[row, col, :] = img[y, x, :]
# 如果想改变输出图像方向,旋转就行了
# line_image = cv2.rotate(line_image, cv2.ROTATE_90_CLOCKWISE)
return line_image
# ----- 主程序
def main(imgpath):
# 读取图像
img = cv2.imread(imgpath)
if img is None:
print("please check image path")
return
# 图像重置为固定大小
img = cv2.resize(img, (HEIGHT, WIDTH))
print(img.shape)
# 展示原图
cv2.imshow("src", img)
output = create_line_image(img)
# 展示结果
cv2.imshow("dst", output)
cv2.waitKey()
cv2.destroyAllWindows()
if __name__ == '__main__':
# 输入图像路径
imgpath = "./image/clock.jpg"
main(imgpath)
结果如下图所示。展开后的矩形图像从左往右对应圆环区域图像从3点钟开始逆时针旋转,矩形图像从上往下对应圆环区域图像从外往里。

2.3 任意角度圆形转换
如果我们想以任意角度进行圆形转换,比如从7点钟方向开始逆时针将圆形展为方形。如下图所示:
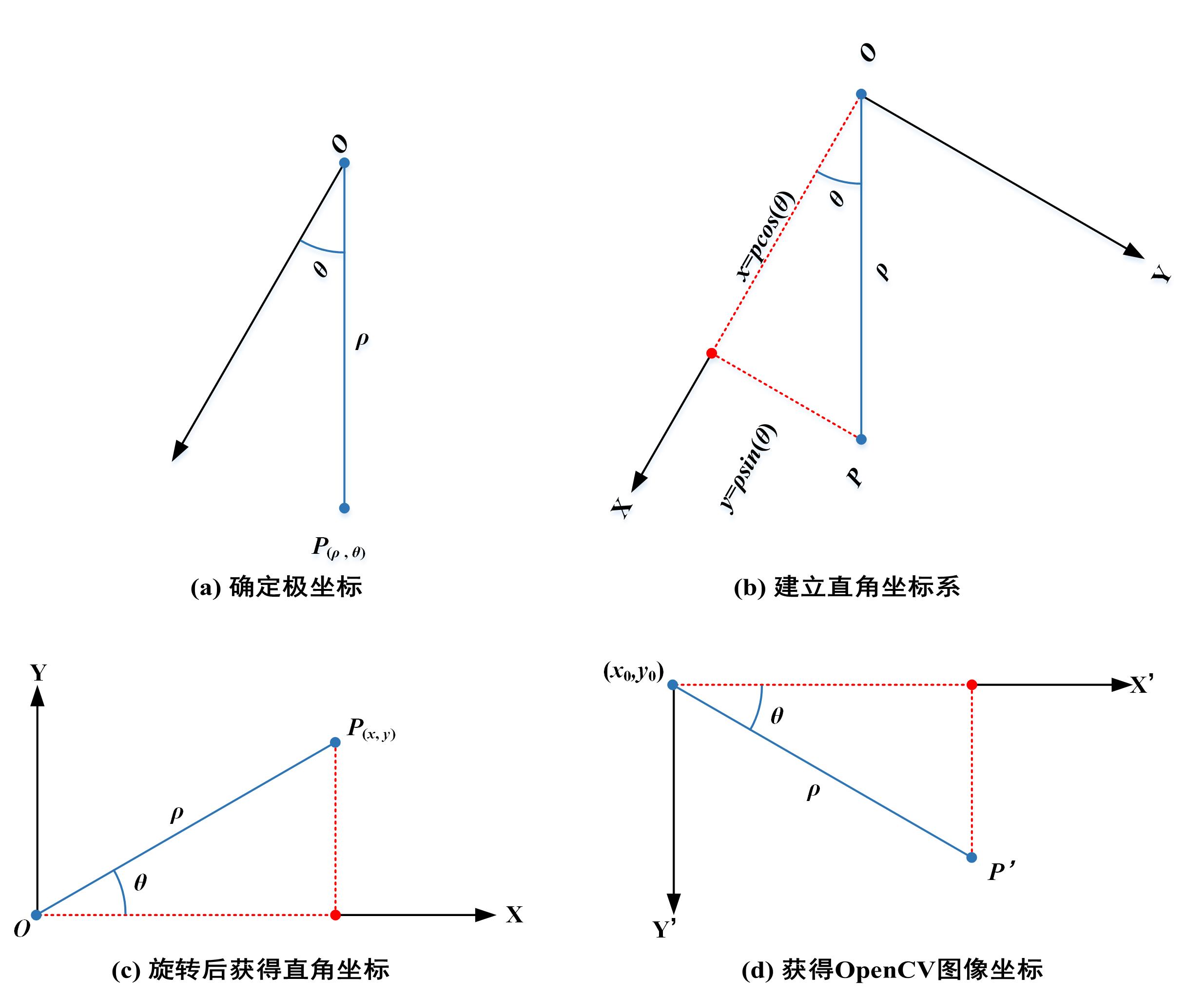
我们需要在以开始转换方向即7点钟轴为极轴建立极坐标系,确定极坐标后,需要建立直角坐标系,然后旋转直角坐标系获得正常直角坐标系的坐标。直接看代码修改create_line_image函数中的转换代码就行。注意7点钟位置相对3点钟位置,角度是240度或者-120度。
C++
cv::Mat create_line_image(cv::Mat img)
{
cv::Mat line_image = cv::Mat::zeros(Size(LINE_WIDTH, LINE_HEIGHT), CV_8UC3);
// 角度
double theta;
// 半径
double rho;
// 按照圆的极坐标赋值
for (int row = 0; row < line_image.rows; row++)
{
for (int col = 0; col < line_image.cols; col++)
{
// 最后的-0.2是用于优化结果,可以自行调整
theta = PI * 2 / LINE_WIDTH * (col + 1) - 0.2;
rho = CIRCLE_RADIUS - row - 1;
// 1 确定极坐标
double x0 = rho * std::cos(theta) + 0;
double y0 = rho * std::sin(theta) + 0;
// 2 确定旋转角度
double angle = PI * 2 * (-120.0) / 360;
// 3 确定直角坐标
double x1 = x0 * std::cos(angle) - y0 * std::sin(angle);
double y1 = x0 * std::sin(angle) + y0 * std::cos(angle);
// 4 切换为OpenCV图像坐标
int x = int(CIRCLE_CENTER.x + x1);
int y = int(CIRCLE_CENTER.y - y1);
// Obtain pixel at(y,x)直接访问像素数据(效率不高,可以修改)
Pixel pixel = img.at<Pixel>(y, x);
// 赋值
line_image.at<Pixel>(row, col) = pixel;
}
}
// 如果想改变输出图像方向,旋转就行了
// cv::rotate(line_image, line_image, cv::ROTATE_90_CLOCKWISE);
return line_image;
}
Python
# ----- 将圆环变为矩形
def create_line_image(img):
# 建立展开后的图像
line_image = np.zeros((LINE_HEIGHT, LINE_WIDTH, 3), dtype=np.uint8)
# 按照圆的极坐标赋值
for row in range(line_image.shape[0]):
for col in range(line_image.shape[1]):
# 角度,最后的-0.2是用于优化结果,可以自行调整
theta = PI * 2 / LINE_WIDTH * (col + 1)-0.2
# 半径,减1防止超界
rho = CIRCLE_RADIUS - row - 1
# 基础变换
# x = int(CIRCLE_CENTER[0] + rho * math.cos(theta) + 0.0)
# y = int(CIRCLE_CENTER[1] - rho * math.sin(theta) + 0.0)
# 1 确定极坐标
x0 = rho * math.cos(theta) + 0.0
y0 = rho * math.sin(theta) + 0.0
# 2 确定旋转角度
angle = math.pi* (-120) / 360 * 2
# 3 确定直角坐标
x1 = x0*math.cos(angle)-y0*math.sin(angle)
y1 = x0*math.sin(angle)+y0*math.cos(angle)
# 4 切换为OpenCV图像坐标
x = int(CIRCLE_CENTER[0] + x1)
y = int(CIRCLE_CENTER[1] - y1)
# 赋值
line_image[row, col, :] = img[y, x, :]
# 如果想改变输出图像方向,旋转就行了
# line_image = cv2.rotate(line_image, cv2.ROTATE_90_CLOCKWISE)
return line_image
结果如下图所示。展开后的矩形图像从左往右对应圆环区域图像从7点钟开始逆时针旋转,矩形图像从上往下对应圆环区域图像从外往里。

2.4 任意角度圆形顺时针转换
如果我们想以任意角度进行圆形顺时针转换,比如从5点钟方向开始顺时针将圆形展为方形。如下图所示:
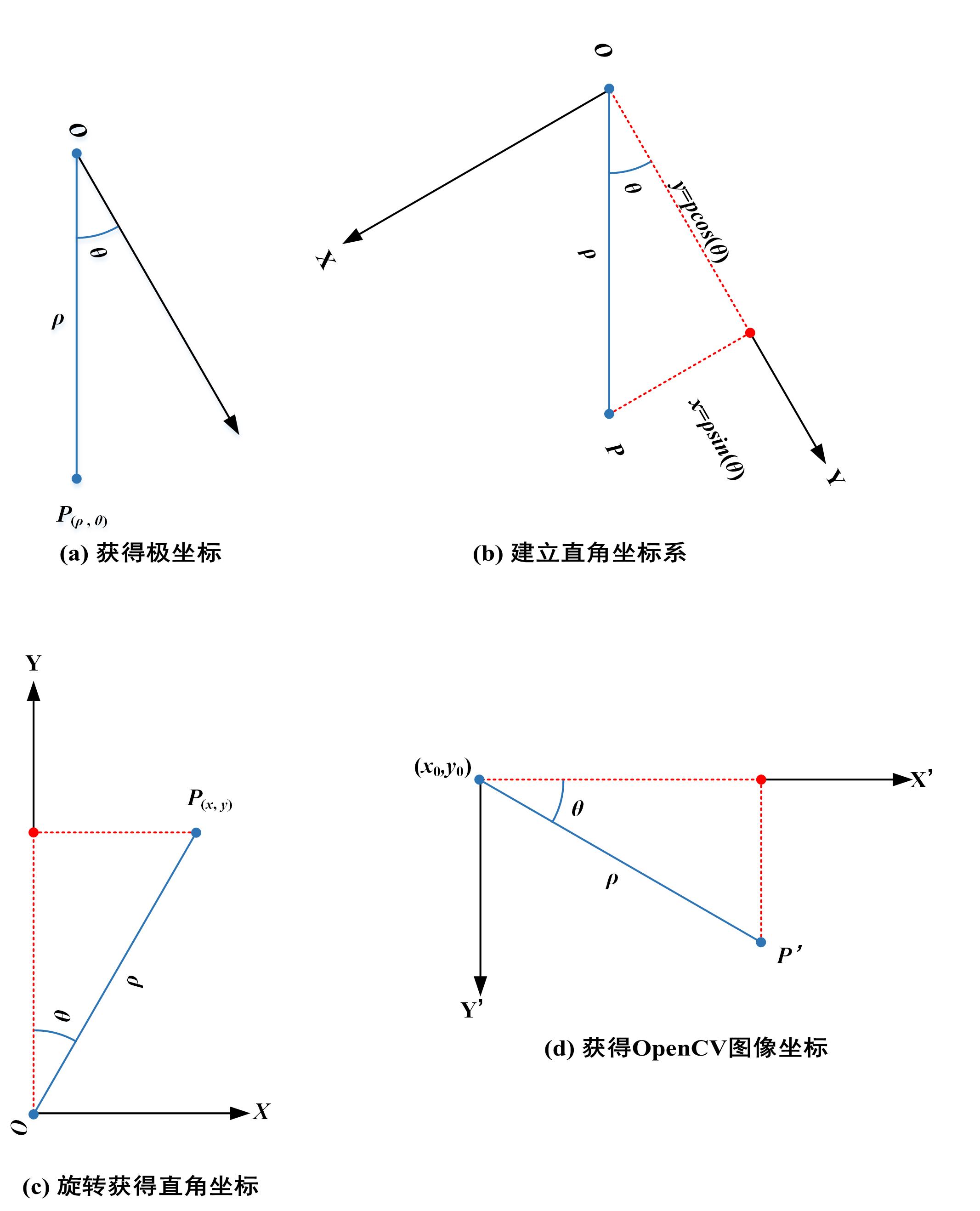
顺时针旋转和逆时针旋转不同,我们需要重新确定极坐标后,然后建立直角坐标系,在这个直角坐标系中,极轴对应y轴,与顺时针变换正好相反。接下来步骤与逆时针旋转是一样的,再旋转直角坐标系获得正常直角坐标系的坐标。直接看代码修改create_line_image函数中的转换代码就行。注意7点钟位置相对5点钟位置,角度是210度或者-150度。
C++
cv::Mat create_line_image(cv::Mat img)
{
cv::Mat line_image = cv::Mat::zeros(Size(LINE_WIDTH, LINE_HEIGHT), CV_8UC3);
// 角度
double theta;
// 半径
double rho;
// 按照圆的极坐标赋值
for (int row = 0; row < line_image.rows; row++)
{
for (int col = 0; col < line_image.cols; col++)
{
// 最后的-0.2是用于优化结果,可以自行调整
theta = PI * 2 / LINE_WIDTH * (col + 1) - 0.2;
rho = CIRCLE_RADIUS - row - 1;
// ----- 任意起始位置顺时针变换
// 1 确定极坐标
double x0 = rho * std::sin(theta) + 0;
double y0 = rho * std::cos(theta) + 0;
// 2 确定旋转角度
double angle = PI * 2 * (-150.0) / 360;
// 3 确定直角坐标
double x1 = x0 * std::cos(angle) - y0 * std::sin(angle) + 0;
double y1 = x0 * std::sin(angle) + y0 * std::cos(angle) + 0;
// 4 切换为opencv图像坐标
int x = int(CIRCLE_CENTER.x + x1);
int y = int(CIRCLE_CENTER.y - y1);
// Obtain pixel at(y,x)直接访问像素数据(效率不高,可以修改)
Pixel pixel = img.at<Pixel>(y, x);
// 赋值
line_image.at<Pixel>(row, col) = pixel;
}
}
// 如果想改变输出图像方向,旋转就行了
// cv::rotate(line_image, line_image, cv::ROTATE_90_CLOCKWISE);
return line_image;
}
Python
# ----- 将圆环变为矩形
def create_line_image(img):
# 建立展开后的图像
line_image = np.zeros((LINE_HEIGHT, LINE_WIDTH, 3), dtype=np.uint8)
# 按照圆的极坐标赋值
for row in range(line_image.shape[0]):
for col in range(line_image.shape[1]):
# 角度,最后的-0.2是用于优化结果,可以自行调整
theta = PI * 2 / LINE_WIDTH * (col + 1)-0.2
# 半径,减1防止超界
rho = CIRCLE_RADIUS - row - 1
# ----- 任意起始位置顺时针变换
# 1 确定极坐标
x0 = rho * math.sin(theta) + 0.0
y0 = rho * math.cos(theta) + 0.0
# 2 确定旋转角度
angle = math.pi* (-150) / 360 * 2
# 3 确定直角坐标
x1 = x0*math.cos(angle)-y0*math.sin(angle) + 0
y1 = x0*math.sin(angle)+y0*math.cos(angle) + 0
# 4 切换为OpenCV图像坐标
x = int(CIRCLE_CENTER[0] + x1)
y = int(CIRCLE_CENTER[1] - y1)
# 赋值
line_image[row, col, :] = img[y, x, :]
# 如果想改变输出图像方向,旋转就行了
# line_image = cv2.rotate(line_image, cv2.ROTATE_90_CLOCKWISE)
return line_image
结果如下图所示。展开后的矩形图像从左往右对应圆环区域图像从5点钟开始顺时针旋转,矩形图像从上往下对应圆环区域图像从外往里。

3 OpenCV内置函数实现图像极坐标变换与逆变换
第二部分我们描述了如何实现图像极坐标转换为直角坐标。但是相应直角坐标转换为极坐标在本文并不会进行具体描述,因为OpenCV有内置函数来实现逆变换(逆变换真要自己写公式倒过来就行了)。OpenCV中包含内置函数可以实现极坐标变换,极坐标逆变换,半对数极坐标变换以及半对数极坐标逆变换。OpenCV提供的函数仅实现3点钟方向开始,逆时针转换为直角坐标,但是提供的函数稳定性比自己写的要好。
其中对数极坐标其实就是将直角坐标转换成极坐标,然后对极长 ρ \rho ρ求取对数,获得的坐标。对数极坐标可以压缩信息,聚焦于关键信息,常用于图像匹配,具体介绍见LogPolar对数极坐标。注意我们常说的对数极坐标一般是半对数极坐标,即只对极长求对数,不对极角求对数。此外还有半对数直角坐标,半对数直角坐标指的是一个轴是分度均匀的普通坐标轴,另一个轴是分度不均匀的对数坐标轴。
在老版本OpenCV中我们通过logPolar和linearPolar来分别实现对数极坐标转换和极坐标转换。但是新版本中用warpPolar函数来代替这两个函数的功能。warpPolar函数的接口如下:
C++:
void cv::warpPolar(
InputArray src,
OutputArray dst,
Size dsize,
Point2f center,
double maxRadius,
int flags)
Python:
dst = cv.warpPolar(src, dsize, center, maxRadius, flags[, dst])
其中src是输入图像,dst是输出图像,dsize为输出图像尺寸,center要变换的边界圆的圆点坐标, maxRadius要变换的边界圆的半径,flags为标志。
对于dsize在C++中可以输入Size(),在Python中可以输入None,表示由OpenCV自行决定输出尺寸。flags为插值方法标志InterpolationFlags和转换方法标志WarpPolarMode的组合。InterpolationFlags具体介绍见官方文档InterpolationFlags。WarpPolarMode表示转换的方法,具体有三种:
- WARP_POLAR_LINEAR以选择线性极坐标映射(默认)。
- WARP_POLAR_LOG以选择半对数极坐标映射。
- WARP_INVERSE_MAP进行反向映射。
这一部分示例代码参考OpenCV自带示例代码polar_transforms。示例代码如下:
C++
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
int main()
{
// log_polar_img 半对数极坐标变换结果
// lin_polar_img 极坐标变换结果
// recovered_log_polar 半对数极坐标逆变换结果
// recovered_lin_polar_img 极坐标逆变换结果
Mat log_polar_img, lin_polar_img, recovered_log_polar, recovered_lin_polar_img;
// INTER_LINEAR 双线性插值,WARP_FILL_OUTLIERS填充所有目标图像像素
int flags = INTER_LINEAR + WARP_FILL_OUTLIERS;
// 读图
String imagepath = "image/clock.jpg";
Mat src = imread(imagepath);
if (src.empty())
{
fprintf(stderr, "Could not initialize capturing...\n");
return -1;
}
// 圆心坐标
Point2f center((float)src.cols / 2, (float)src.rows / 2);
// 圆的半径
double maxRadius = min(center.y, center.x);
// direct transform
// linear Polar 极坐标变换, Size()表示OpenCV根据输入自行决定输出图像尺寸
warpPolar(src, lin_polar_img, Size(), center, maxRadius, flags);
// semilog Polar 半对数极坐标变换, Size()表示OpenCV根据输入自行决定输出图像尺寸
warpPolar(src, log_polar_img, Size(), center, maxRadius, flags + WARP_POLAR_LOG);
// inverse transform 逆变换
warpPolar(lin_polar_img, recovered_lin_polar_img, src.size(), center, maxRadius, flags + WARP_INVERSE_MAP);
warpPolar(log_polar_img, recovered_log_polar, src.size(), center, maxRadius, flags + WARP_POLAR_LOG + WARP_INVERSE_MAP);
// 改变结果方向
// rotate(lin_polar_img, lin_polar_img, ROTATE_90_CLOCKWISE);
// 展示图片
imshow("Src frame", src);
imshow("Log-Polar", log_polar_img);
imshow("Linear-Polar", lin_polar_img);
imshow("Recovered Linear-Polar", recovered_lin_polar_img);
imshow("Recovered Log-Polar", recovered_log_polar);
waitKey(0);
system("pause");
return 0;
Python
import cv2
# ----- 主函数
def main():
# INTER_LINEAR 双线性插值,WARP_FILL_OUTLIERS填充所有目标图像像素
flags = cv2.INTER_LINEAR | cv2.WARP_FILL_OUTLIERS
# 读图
imagepath = "image/clock.jpg"
src = cv2.imread(imagepath)
if src is None:
print("Could not initialize capturing...\n")
return -1
# 圆心坐标
center = (float(src.shape[0] / 2), float(src.shape[1] / 2))
# 圆的半径
maxRadius = min(center[0], center[1])
# direct transform
# linear Polar 极坐标变换, None表示OpenCV根据输入自行决定输出图像尺寸
lin_polar_img = cv2.warpPolar(src, None, center, maxRadius, flags)
# semilog Polar 半对数极坐标变换, None表示OpenCV根据输入自行决定输出图像尺寸
log_polar_img = cv2.warpPolar(src, None, center, maxRadius, flags | cv2.WARP_POLAR_LOG)
# inverse transform 逆变换
recovered_lin_polar_img = cv2.warpPolar(lin_polar_img, (src.shape[0], src.shape[1]), center, maxRadius,
flags | cv2.WARP_INVERSE_MAP)
recovered_log_polar = cv2.warpPolar(log_polar_img, (src.shape[0], src.shape[1]), center, maxRadius,
flags | cv2.WARP_POLAR_LOG | cv2.WARP_INVERSE_MAP)
# 改变结果方向
# lin_polar_img = cv2.rotate(lin_polar_img, cv2.ROTATE_90_CLOCKWISE)
# 展示图片
cv2.imshow("Src frame", src)
cv2.imshow("Log-Polar", log_polar_img)
cv2.imshow("Linear-Polar", lin_polar_img)
cv2.imshow("Recovered Linear-Polar", recovered_lin_polar_img)
cv2.imshow("Recovered Log-Polar", recovered_log_polar)
cv2.waitKey(0)
return 0
if __name__ == '__main__':
main()
结果如下所示。OpenCV自带转换函数是直接以3点钟方向为起点顺时针变换,只考虑标准直角坐标系。对数坐标会大大压缩信息,所以对数坐标逆变换后的结果图像会模糊,但是圆转方会把原图中面积较大的区域更多的显示出来。此外OpenCV自带转换函数圆转方输出的是从上到小的结果,图像旋转下就可以得到第二节的结果。
| 方法 | 图像 |
|---|---|
| 对数极坐标变换 |  |
| 极坐标变换 |  |
| 对数极坐标逆变换 |  |
| 极坐标逆变换 |  |
4 参考
4.1 基础数学
4.2 代码
本文来自博客园,作者:落痕的寒假,转载请注明原文链接:https://www.cnblogs.com/luohenyueji/p/16970212.html





