LeetCode算法题-栈类
1.给定一个二叉树，返回它的中序遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,3,2]
进阶: 递归算法很简单，你可以通过迭代算法完成吗？
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-inorder-traversal
关键点和易错点：
（1）这道题如果用递归来做那么很简单，几行代码即可且很容易理解，难的是怎么用非递归的思想来做，这里有两种非递归的算法来做
（2）使用栈来协助，思想是把节点放到栈里去，由栈来控制节点的输出顺序，我的思想一个节点先push进去，如果有左节点则继续push左节点，一直到没有左节点，然后pop出一个节点，并指向它右节点进行新一轮push判断，如果是空则再pop直到队列为空且没有其它节点了，仔细想想这个过程其实就是左中右的顺序
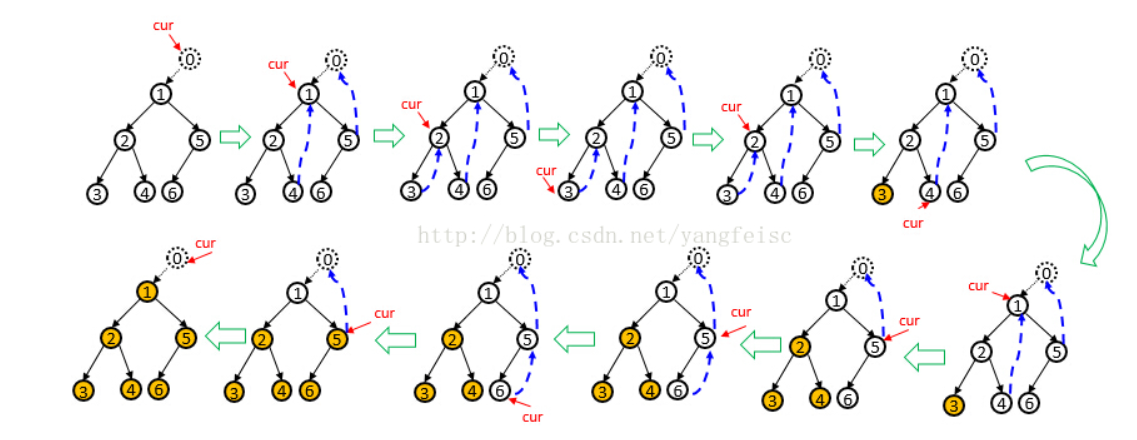
（3）另外一种难想的算法是莫里斯遍历算法，它的思想是把它变成一个线索二叉树，如下：
1
/ \
2 3
/ \ /
4 5 6
变成
4
\
2
\
5
\
1
\
3
/
6
变化算法：
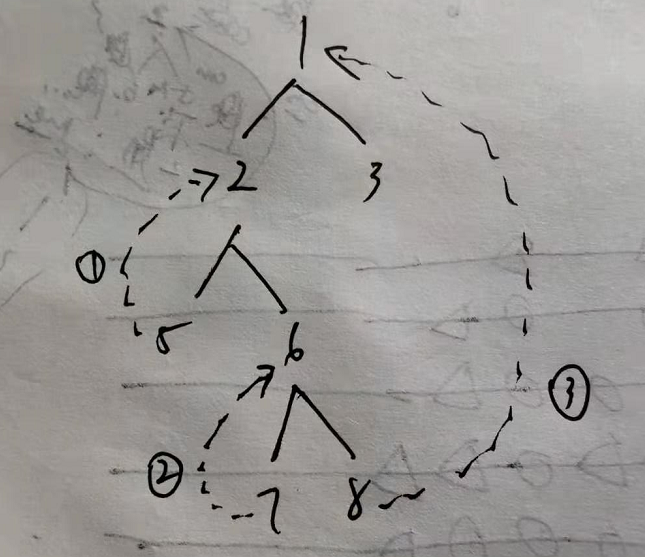
（1）把1置为cur，如果cur有左孩子，则左孩子置为pre，所以2置为pre，然后寻找2的最右节点，比如2个最右节点是5，则pre为5，然后用pre的右孩子指向cur，接着cur被置为2，又开始一轮，就是4指向2，接着cur是4，这时cur没有左孩子了，直接添加到输出列表，且将cur = cur.right，可以看到这时其实是开始回溯了
（2）按（1）这样可以看到其实是有环路的，所以程序里我们会用环路来判断当前是不是出于回溯状态，然后根据这个条件将之前增加的指向（比如之前的5的右孩子指针指向1）置回去，这样便不改变原有树的结构了
以下再给个图，以方便看到这里回溯的思想：
这里是1,2,3,5,6,7,8为例，可以看到当遍历到5时，利用之前构建的环又回到了2，7回到了6，8回到了1
提交代码：
使用栈的算法：
# Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): def inorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ ret_list = [] stack = [] while root or len(stack) > 0: while root: stack.append(root) root = root.left tmp = stack.pop(-1) ret_list.append(tmp.val) root = tmp.right return ret_list
使用莫里斯遍历的算法：
# Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): def inorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ ret_list = [] cur = root while cur: if cur.left is None: ret_list.append(cur.val) cur = cur.right else: pre = cur.left while pre.right is not None and pre.right is not cur: pre = pre.right if pre.right is None: pre.right = cur cur = cur.left else: ret_list.append(cur.val) pre.right = None cur = cur.right return ret_list
同理，如果是前序遍历：
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal
则使用栈的辅助算法：
class Solution(object): def preorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ ret_list = [] stack = [] while root or len(stack) > 0: while root: ret_list.append(root.val) stack.append(root) root = root.left tmp = stack.pop(-1) root = tmp.right return ret_list
使用莫里斯遍历算法（跟之前中序遍历几乎一样，只是改了输出位置）：
class Solution(object): def preorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ ret_list = [] cur = root while cur: if cur.left is None: ret_list.append(cur.val) cur = cur.right else: pre = cur.left while pre.right is not None and pre.right is not cur: pre = pre.right if pre.right is None: ret_list.append(cur.val) pre.right = cur cur = cur.left else: pre.right = None cur = cur.right return ret_list
如果是后序遍历：
使用栈的还是同样的思路，不过需要再加一个栈来判断该节点的右子节点是否是已经遍历过了：
class Solution(object): def postorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ ret_list = [] stack = [] right_stack = [] while root or len(stack) > 0: while root: stack.append(root) root = root.left tmp = stack.pop(-1) if tmp.right: right_stack_len = len(right_stack) if right_stack_len > 0 and right_stack[right_stack_len-1] is tmp: ret_list.append(right_stack.pop(-1).val) else: right_stack.append(tmp) stack.append(tmp) root = tmp.right else: ret_list.append(tmp.val) return ret_list
使用莫里斯思想就比较难想到了，需要加一个虚拟节点指向根节点，不然逻辑复杂，每一次判断到环那里有个遍历右节点并翻转值存入到输出结果中的操作，这样的话运行速度其实还是双栈的会快一一点：
思维图（那个0是虚拟节点）：
class Solution(object): def postorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ ret_list = [] vir_node = TreeNode(0) vir_node.left = root cur = vir_node while cur: if cur.left is None: cur = cur.right else: pre = cur.left while pre.right is not None and pre.right is not cur: pre = pre.right if pre.right is None: pre.right = cur cur = cur.left else: tmp_list = [] pre.right = None t = cur.left while t: tmp_list.append(t.val) t = t.right ret_list.extend(tmp_list[::-1]) cur = cur.right vir_node.left = None return ret_list
2.根据逆波兰表示法，求表达式的值。
有效的运算符包括 +, -, *, / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。
说明：
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1：
输入: ["2", "1", "+", "3", "*"]
输出: 9
解释: ((2 + 1) * 3) = 9
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/evaluate-reverse-polish-notation
关键点和易错点：
（1）用python解这道题一定要注意python在对一个是负数一个是正数情况下，值是向下取整的也就是说-5/3是等于-2的，而不是我们理解的-1，所以最好的方法是在除法时将其转换为浮点数来进行运算，然后用int强制类型转换，int强制类型转换int(-0.6)是取值为0的，对负数来说是向上取整了
提交代码：
class Solution(object): def evalRPN(self, tokens): """ :type tokens: List[str] :rtype: int """ stack = [] for i in tokens: if i in "+-*/": sec_val = stack.pop(-1) fir_val = stack.pop(-1) if i == "+": stack.append(fir_val+sec_val) elif i == "-": stack.append(fir_val-sec_val) elif i == "*": stack.append(fir_val*sec_val) elif i == "/": stack.append(int(float(fir_val)/float(sec_val))) else: stack.append(int(i)) return stack.pop(-1)
3.给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。
例如：
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回锯齿形层次遍历如下：
[
[3],
[20,9],
[15,7]
]
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-zigzag-level-order-traversal
关键点和易错点：
（1）脑海中的第一思维就是用个flag来控制顺序还是反序，但是后面想想没有那么简单，因为访问需要逆序访问时却要它的孩子节点是正序的，就卡在这了，所以我一开始提交的代码还是在列表里做了反序来完成的，这种效率不高
（2）其实这个题目如果用两个栈来做，模拟下你会发现很完美解决这个问题，因为它刚好解决了我一开始的疑惑，访问时逆序，但孩子节点进入另外一个栈后，出来的顺序是正序的
列表反序代码：
class Solution(object): def zigzagLevelOrder(self, root): """ :type root: TreeNode :rtype: List[List[int]] """ ret_list = [] if not root: return ret_list flag = 0 queue_t = [] queue_t.append(root) queue_t.append(None) tmp_list = [] while len(queue_t) > 0: node = queue_t.pop(0) if not node: flag += 1 if flag % 2 != 0: ret_list.append(tmp_list) else: ret_list.append(tmp_list[::-1]) if len(queue_t) == 0: break queue_t.append(None) tmp_list = [] continue tmp_list.append(node.val) if node.left: queue_t.append(node.left) if node.right: queue_t.append(node.right) return ret_list
双栈代码：
class Solution(object): def zigzagLevelOrder(self, root): """ :type root: TreeNode :rtype: List[List[int]] """ ret_list = [] if not root: return ret_list left_stack = [] right_stack = [] left_stack.append(root) tmp_list = [] while len(left_stack) > 0 or len(right_stack) > 0: tmp_list = [] if len(left_stack) > 0: while len(left_stack) > 0: node = left_stack.pop(-1) tmp_list.append(node.val) if node.left: right_stack.append(node.left) if node.right: right_stack.append(node.right) else: while len(right_stack) > 0: node = right_stack.pop(-1) tmp_list.append(node.val) if node.right: left_stack.append(node.right) if node.left: left_stack.append(node.left) ret_list.append(tmp_list) return ret_list
4.设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。
push(x) -- 将元素 x 推入栈中。
pop() -- 删除栈顶的元素。
top() -- 获取栈顶元素。
getMin() -- 检索栈中的最小元素。
示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/min-stack
关键点和易错点：
（1）这道题看似很简单，但是如果想要使用巧妙的解法解决，还是比较难想到的，我一开始使用的是一个变量来保存最小值，当该变量被pop出时需要遍历栈中已有值来确定下一个最小值，这里开销就很大了
（2）一般这种可以采用空间换时间的方法，利用一个辅助栈helper，专门用来存放某时刻最小的值，这样不管怎么pop我这个辅助栈都保证pop完之后该辅助栈的最上层的值是当前最小的那个，这其实也就利用了栈的顺序特性来解决
提交代码：
class MinStack(object): def __init__(self): """ initialize your data structure here. """ self.data = [] self.helper = [] def push(self, x): """ :type x: int :rtype: None """ self.data.append(x) if len(self.helper) == 0 or x <= self.helper[-1]: self.helper.append(x) def pop(self): """ :rtype: None """ tmp = self.data.pop(-1) if len(self.helper) > 0 and tmp == self.helper[-1]: self.helper.pop(-1) def top(self): """ :rtype: int """ if len(self.data) > 0: return self.data[-1] def getMin(self): """ :rtype: int """ if len(self.helper): return self.helper[-1]
5.实现一个基本的计算器来计算一个简单的字符串表达式的值。
字符串表达式可以包含左括号 ( ，右括号 )，加号 + ，减号 -，非负整数和空格 。
示例 1:
输入: "1 + 1"
输出: 2
示例 2:
输入: " 2-1 + 2 "
输出: 3
示例 3:
输入: "(1+(4+5+2)-3)+(6+8)"
输出: 23
说明：
你可以假设所给定的表达式都是有效的。
请不要使用内置的库函数 eval。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/basic-calculator
关键点和易错点：
（1）这道题脑海中首先想到的是先转换为逆波兰表达式再后缀表达式求解，但其实这种方法对于该道题需求来说简直把它弄复杂了，因为这道题只有+-运算符，没有乘除
（2）其实可以通过拆括号的思维来解，因为它只有加减
逆波兰方式：
class Solution(object): def calculate(self, s): """ :type s: str :rtype: int """ ret_list = self.translate_postfix_expre(s) return self.cal_postfix_expre(ret_list) def translate_postfix_expre(self, s): symbol_stack = [] ret_list = [] num = None for c in s: if c == ' ': continue elif c in '+-()': if num is not None: ret_list.append(num) num = None if c in '+-': while len(symbol_stack) > 0 and symbol_stack[-1] != '(': ret_list.append(symbol_stack.pop(-1)) symbol_stack.append(c) elif c == ')': while len(symbol_stack) > 0 and symbol_stack[-1] != '(': ret_list.append(symbol_stack.pop(-1)) symbol_stack.pop(-1) else: symbol_stack.append(c) else: if num is None: num = 0 num = num * 10 + int(c) if num is not None: ret_list.append(num) while len(symbol_stack) > 0: ret_list.append(symbol_stack.pop(-1)) return ret_list def cal_postfix_expre(self, s_list): num_stack = [] for i in s_list: if i == '+' or i == '-': sec_num = num_stack.pop(-1) fir_num = num_stack.pop(-1) if i == '+': num_stack.append(fir_num+sec_num) else: num_stack.append(fir_num-sec_num) else: num_stack.append(i) return num_stack[-1]
拆括号方式：
class Solution(object): def calculate(self, s): """ :type s: str :rtype: int """ convert_stack = [] num = 0 ret_result = 0 pre_op = '+' actual_pre_op = '+' for i in s: if i == ' ': continue elif i in '+-': actual_pre_op = i ret_result = ret_result + num if pre_op == '+' else ret_result - num num = 0 if len(convert_stack) > 0 and convert_stack[-1] == True: pre_op = '+' if i == '-' else '-' else: pre_op = i elif i == '(': if len(convert_stack) > 0: if actual_pre_op == '-': convert_stack.append(not convert_stack[-1]) else: convert_stack.append(convert_stack[-1]) else: if actual_pre_op == '-': convert_stack.append(True) else: convert_stack.append(False) elif i == ')': convert_stack.pop(-1) else: num = num * 10 + int(i) if num > 0: ret_result = ret_result + num if pre_op == '+' else ret_result - num return ret_result
6.使用队列实现栈的下列操作：
push(x) -- 元素 x 入栈
pop() -- 移除栈顶元素
top() -- 获取栈顶元素
empty() -- 返回栈是否为空
注意:
你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。 你可以使用 list 或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。
你可以假设所有操作都是有效的（例如, 对一个空的栈不会调用 pop 或者 top 操作）。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/implement-stack-using-queues
关键点和易错点：
（1）一开始想到的就是复杂度比较高的实现，复杂度为O(n)，觉得不可能这么高的开销，想了较久，后面看了下题解，发现就是这样，要么入栈复杂度O(n)，要么就出栈负责度O(n)
（2）这道题就是警醒下，不要觉得复杂度高就不是正解，自信点可能就是只有这种解法了
（3）还有1题是类似这题的是用栈来模拟队列操作，那个在摊还（一次最坏的情况发生后，在较久的时候内不会再发生）下能做到O(1)
提交代码：
class MyStack(object): def __init__(self): """ Initialize your data structure here. """ self.q1 = [] def push(self, x): """ Push element x onto stack. :type x: int :rtype: None """ q1_size = len(self.q1) self.q1.append(x) while q1_size > 0: self.q1.append(self.q1.pop(0)) q1_size -= 1 def pop(self): """ Removes the element on top of the stack and returns that element. :rtype: int """ return self.q1.pop(0) def top(self): """ Get the top element. :rtype: int """ return self.q1[0] def empty(self): """ Returns whether the stack is empty. :rtype: bool """ if len(self.q1) == 0: return True return False
7.给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。
在 S 上反复执行重复项删除操作，直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例：
输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。
提示：
1 <= S.length <= 20000
S 仅由小写英文字母组成。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/remove-all-adjacent-duplicates-in-string
关键点和易错点：
（1）想到用栈就很简单了，难点在于有没有想到栈去解决这个问题
提交代码：
class Solution(object): def removeDuplicates(self, S): """ :type S: str :rtype: str """ stack = [] for c in S: if len(stack) > 0 and stack[-1] == c: stack.pop() else: stack.append(c) return ''.join(stack)
8.接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/trapping-rain-water
关键点和易错点：
思路分析：
（1）问题在没有进行分析前觉得有点复杂，不知从何下手，但其实只要对着图模拟试下就会发现一些规律，比如当前面有一个更高的点的时候假设是a这个点，那么a点之前的比a点矮的点对a点之后的点都是没有意义的了，可以提前结算这些点了，结算规则（假设把之前的点都存放到栈中，且栈的元素以(x,y)的形式保存，比如[2,4,6]的点保存时就是(0,2)、(1,4)和(2,6)，其实就是记住横坐标，高是竖坐标，这样方便后面计算矩形面积）：
<1>如果栈里元素大于1，且a点比栈顶元素大（如果比栈顶元素小就入栈），则pop出栈顶元素并累加该点占的面积到des_tmp变量（因为栈元素低到高是从大到小的，所以栈里元素肯定还有比该点高的点，所以这个点注定是要被雨水淹没的，所以这里累积就是留给后面用总的减去这些淹没的点的面积），然后再循环判断栈顶元素和a点的值（注意：下面的图的1，2，3，4并不是代表高度，只是代表第1，2，3，4个柱形）
这里的2，3，柱形就是被淹没的，4就是上文说的a点
<2>如果栈里元素为1且a点元素比栈顶元素大，说明栈里元素都需清掉了，可以结算a点前接到的雨水了，pop出栈的最后一个点并直接用该点和a点计算它们形成的矩形面积即可（淹没掉的那些点的面积在第<1>步计算过保存在des_tmp变量了，用以最后减去），然后a点入栈，这样a点就相当于又是新的第一个点了
这种情况就是4这个点是a点，然后前面的点都没有这个点高，进行前面点的结算，4这个点成为新的第一个节点
（2）如果后面一直遇到的点都是比栈顶小的，遍历完这些点后则会形成栈底到顶是从大到小的点，所以会有如下图这种情形，这种情形就更好计算了，直接每次pop出一个然后与栈顶计算它们之间的矩形面积然后累加到result变量中
这个情况就是遍历完了，还剩余在栈里的点，两两结算积的雨量
（3）最后用result减去des_tmp变量则是接到的总的雨水量了
个人易错点：
（1）横坐标和竖坐标搞反了，比如：
result += ((x_num - stack[-1][0] - 1) * stack[-1][1])里的stack[-1][0]写成了stack[-1][1]
（2）最后判断那里取小高度那里没注意result += ((last_one[0] - last_sec_one[0] - 1) * last_sec_one[1])里的last_sec_one[1]写成了last_one[1]
提交代码：
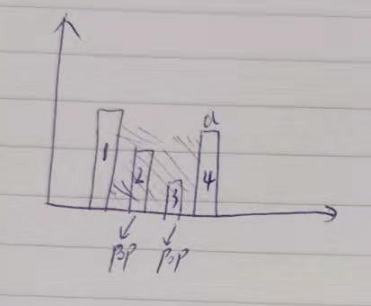
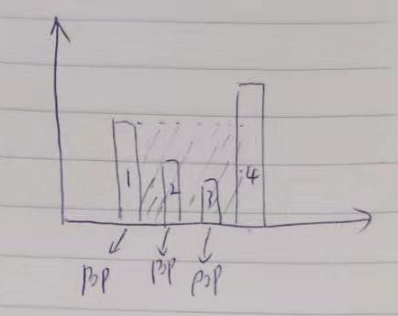
class Solution(object): def trap(self, height): """ :type height: List[int] :rtype: int """ stack = [] result = 0 des_tmp = 0 x_num = 0 for i in height: x_num += 1 if len(stack) > 0 and stack[-1][1] < i: while len(stack) > 1 and stack[-1][1] < i: des_tmp += stack[-1][1] stack.pop() if len(stack) == 1 and stack[-1][1] < i: result += ((x_num - stack[-1][0] - 1) * stack[-1][1]) stack.pop() stack.append((x_num, i)) while len(stack) > 1: last_one = stack.pop() last_sec_one = stack[-1] result += ((last_one[0] - last_sec_one[0] - 1) * last_one[1]) return result-des_tmp
9.简化路径
以 Unix 风格给出一个文件的绝对路径，你需要简化它。或者换句话说，将其转换为规范路径。
在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点 （..） 表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。更多信息请参阅：Linux / Unix中的绝对路径 vs 相对路径
请注意，返回的规范路径必须始终以斜杠 / 开头，并且两个目录名之间必须只有一个斜杠 /。最后一个目录名（如果存在）不能以 / 结尾。此外，规范路径必须是表示绝对路径的最短字符串。
示例 1：
输入："/home/"
输出："/home"
解释：注意，最后一个目录名后面没有斜杠。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/simplify-path
关键点和易错点：
（1）如果按照常规的那样去做会有非常多的条件判断，很容易发生bug从而提交失败
（2）换种简单明了的思路，用分割“/”的方法并采用栈保存文件夹名
提交代码：
class Solution(object): def simplifyPath(self, path): """ :type path: str :rtype: str """ ret = [] path_list = path.split('/') for l in path_list: if l == "" or l == ".": continue elif l == "..": if len(ret) > 0: ret.pop() else: ret.append(l) return "/"+"/".join(ret)
10.柱状图中最大的矩形
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram
关键点和易错点：
（1）这道题做了接近2.5小时才提交成功，一开始自己想的方法思路跟官方的差不多，但由于自己维护了一个宽度，导致超时，但其实宽度不用自己维护，完全可以通过计算得到
这里说下我的第一种解法超时的易错地方：
num += tmp[1]这里很容易想成num += +1了，虽然这num += tmp[1]也不对
num = tmp[1] + 1这里想成num += tmp[1]，这样会重复计算，应该只要刚好比它大的那个就行
（2）思路就是遇到一个比前面的矮的时候，高的那些需要pop出来，因为已经不连续了，只能以小于等于这个矮的高度的可以继续计算
（3）栈里保存的是字符串的下标，不是高度值，这里很容易搞错
维护宽度导致超时的提交代码（还做了个剪枝）：
class Solution(object): def largestRectangleArea(self, heights): """ :type heights: List[int] :rtype: int """ stack = [] max_area = 0 heights_len = len(heights) for i in range(0, heights_len): if len(stack) == 0: if heights[i]*(heights_len-i) > max_area: stack.append([heights[i], 1]) else: num = 1 while len(stack) > 0 and stack[-1][0] > heights[i]: tmp = stack.pop() num = tmp[1] + 1 max_area = max(tmp[0]*tmp[1], max_area) for j in range(0, len(stack)): stack[j][1] += 1 if len(stack) == 0 or stack[-1][0] != heights[i]: if heights[i]*(heights_len-i-1+num) > max_area: stack.append([heights[i], num]) while len(stack) > 0: tmp = stack.pop() max_area = max(tmp[0]*tmp[1], max_area) return max_area
正确的通过计算宽度来做的：
class Solution(object): def largestRectangleArea(self, heights): """ :type heights: List[int] :rtype: int """ stack = [-1] max_area = 0 heights_len = len(heights) for i in range(0, heights_len): while len(stack) > 1 and heights[stack[-1]] >= heights[i]: tmp = stack.pop() max_area = max(heights[tmp] * (i-stack[-1]-1), max_area) stack.append(i) while len(stack) > 1: tmp = stack.pop() max_area = max(heights[tmp] * (heights_len-stack[-1]-1), max_area) return max_area
11.比较含退格的字符串
给定 S 和 T 两个字符串，当它们分别被输入到空白的文本编辑器后，判断二者是否相等，并返回结果。 # 代表退格字符。
示例 1：
输入：S = "ab#c", T = "ad#c"
输出：true
解释：S 和 T 都会变成 “ac”。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/backspace-string-compare
关键点和易错点：
（1）这道题很容易想到用栈来解决，快速且不易错，就是需要空间复杂度O(m+n)
（2）还有一种方法没那么容易想到，从尾部判断起，空间复杂度为O(1)
栈方法：
class Solution(object): def backspaceCompare(self, S, T): """ :type S: str :type T: str :rtype: bool """ s_stack = [] t_stack= [] for tmp_s in S: if tmp_s == '#': if len(s_stack) > 0: s_stack.pop() else: s_stack.append(tmp_s) for tmp_t in T: if tmp_t == '#': if len(t_stack) > 0: t_stack.pop() else: t_stack.append(tmp_t) if len(s_stack) != len(t_stack): return False while len(s_stack) > 0: if s_stack.pop() != t_stack.pop(): return False return True
尾部遍历方法：
class Solution(object): def backspaceCompare(self, S, T): """ :type S: str :type T: str :rtype: bool """ i = len(S) -1 j = len(T) - 1 while i >= 0 or j >= 0: def find_vaild_c(X, point): flag = 0 while point >= 0 and flag <= 0: if X[point] == '#': flag -= 1 else: flag += 1 if flag <= 0: point -= 1 return point i = find_vaild_c(S, i) j = find_vaild_c(T, j) if not ((i < 0 and j < 0) or (i >= 0 and j >= 0 and S[i] == T[j])): return False i -= 1 j -= 1 return True
12.验证二叉树的前序序列化
序列化二叉树的一种方法是使用前序遍历。当我们遇到一个非空节点时，我们可以记录下这个节点的值。如果它是一个空节点，我们可以使用一个标记值记录，例如 #。
_9_
/ \
3 2
/ \ / \
4 1 # 6
/ \ / \ / \
# # # # # #
例如，上面的二叉树可以被序列化为字符串 "9,3,4,#,#,1,#,#,2,#,6,#,#"，其中 # 代表一个空节点。
给定一串以逗号分隔的序列，验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 '#' 。
你可以认为输入格式总是有效的，例如它永远不会包含两个连续的逗号，比如 "1,,3" 。
示例 1:
输入: "9,3,4,#,#,1,#,#,2,#,6,#,#"
输出: true
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/verify-preorder-serialization-of-a-binary-tree
关键点和易错点：
（1）二叉树的特性：null节点的数量肯定是比非null节点多1；空二叉树也是二叉树
（2）我一开始的思路：每个非null节点都会有两个儿子，儿子可以是null，所以非#节点都会有两个儿子，程序围绕计算所有非#节点有两个儿子后都退栈，所以如果是正常二叉树，那么节点肯定是可以全部退出的，最后栈肯定是空的（之后做题一定要第一遍就思考到所有可能的案例，不能依赖判题系统给出的测试用例来找自己的代码漏洞）
（3）我的解法其实过于冗余且思路没那么清晰，虽然有点像模拟前序遍历，但却又不是，下面提供一种真模拟前序遍历的解法
（4）有一种解法是更直观的，一个非#的节点肯定是有两条边的，就跟一个非None的节点一定会有两个儿子（儿子节点可以是#）节点一样
第一次的解法，用了太多冗余特性（剪枝特性还是可以的，根据奇偶数判断来剪枝）：
class Solution(object): def isValidSerialization(self, preorder): """ :type preorder: str :rtype: bool """ null_num = 0 stack = [] target_list = preorder.split(',') target_list_num = len(target_list) if target_list_num % 2 == 0: return False if target_list[0] == "#": if target_list_num == 1: return True else: return False else: stack.append(target_list[0]) pre = target_list[0] for i in range(1, target_list_num): if len(stack) == 0: return False if pre == "#": stack.pop() if target_list[i] == "#": null_num += 1 else: stack.append(target_list[i]) pre = target_list[i] if target_list_num/2 != null_num-1: return False return True
第二次解法优化了下，删掉了一些特性，简化了代码：
class Solution(object): def isValidSerialization(self, preorder): """ :type preorder: str :rtype: bool """ target_list = preorder.split(',') target_list_num = len(target_list) if target_list_num % 2 == 0: return False stack = [] pre = "" for t in target_list: if pre == "#": if len(stack) == 0: return False stack.pop() if t != "#": stack.append(t) pre = t if len(stack) != 0: return False return True
看到别人的更简洁的根据前序遍历出栈的特性做的：
class Solution(object): def isValidSerialization(self, preorder): """ :type preorder: str :rtype: bool """ target_list = preorder.split(',') target_list_num = len(target_list) if target_list_num % 2 == 0: return False stack = [] for t in target_list: while t == "#" and len(stack) > 0 and stack[-1] == "#": stack.pop() if len(stack) == 0: return False stack.pop() stack.append(t) if len(stack) != 1 or stack[-1] != '#': return False return True
根据每个非#节点一定会有两条边原理来做的：
class Solution(object): def isValidSerialization(self, preorder): """ :type preorder: str :rtype: bool """ preorder = preorder.split(",") edges = 1 for item in preorder: edges -= 1 if edges < 0: return False if item != "#": edges += 2 return edges == 0
13.下一个更大元素 II
给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。
示例 1:
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数；
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/next-greater-element-ii
关键点和易错点：
（1）想到两趟入栈即可
（2）在找到分割点后，那个分割点也要包含进第二趟
提交代码：
class Solution(object): def nextGreaterElements(self, nums): """ :type nums: List[int] :rtype: List[int] """ split_point = -1 nums_len = len(nums) stack = [] result = [-1] * nums_len for i in range(0, nums_len): while len(stack) > 0 and nums[i] > nums[stack[-1]]: result[stack[-1]] = nums[i] stack.pop() if len(stack) == 0: split_point = i stack.append(i) j = 0 while len(stack) > 0 and j <= split_point: while len(stack) > 0 and nums[j] > nums[stack[-1]]: result[stack[-1]] = nums[j] stack.pop() j += 1 return result
14.132模式
给定一个整数序列：a1, a2, ..., an，一个132模式的子序列 ai, aj, ak 被定义为：当 i < j < k 时，ai < ak < aj。设计一个算法，当给定有 n 个数字的序列时，验证这个序列中是否含有132模式的子序列。
注意：n 的值小于15000。
示例1:
输入: [-1, 3, 2, 0]
输出: True
解释: 序列中有 3 个132模式的的子序列: [-1, 3, 2], [-1, 3, 0] 和 [-1, 2, 0].
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/132-pattern
关键点和易错点：
（1）一开始想到的方法是利用快速排序的原理来做，但平均复杂度是O(nlgn)
（2）官方的解法很妙，先利用O(n)空间复杂度固定住每个位置的最小值，然后从后来前来遍历，因为此时min_nums保存了每个位置的最小值，然后用一个栈来记录最大值，保持栈的从下到上是从大到小的，因为我们是要栈顶元素值小于当前元素值（因为要k<j），所以只需要比较栈顶即可，栈顶的维护也靠min_nums，min_nums从后到前世逐渐增大的，所以当栈顶的元素小于min_nums[i]就可以pop出淘汰了
（3）感悟：对于栈的问题，一般都是保持栈的低到高是有序的，要么升序，要么降序；如果能用空间负责度降低时间复杂度，那就用吧；对于多个可变因素时应该想办法固定住一个，可以简化问题分析
提交代码：
class Solution(object): def find132pattern(self, nums): """ :type nums: List[int] :rtype: bool """ nums_len = len(nums) if nums_len < 3: return False min_nums = [0] * nums_len min_nums[0] = nums[0] stack = [] for i in range(1, nums_len): min_nums[i] = min(min_nums[i-1], nums[i]) for i in range(nums_len-1, 0, -1): if nums[i] > min_nums[i]: while len(stack) > 0 and stack[-1] <= min_nums[i]: stack.pop() if len(stack) > 0 and nums[i] > stack[-1]: return True stack.append(nums[i]) return False
15.移掉K位数字
给定一个以字符串表示的非负整数 num，移除这个数中的 k 位数字，使得剩下的数字最小。
注意:
num 的长度小于 10002 且 ≥ k。
num 不会包含任何前导零。
示例 1 :
输入: num = "1432219", k = 3
输出: "1219"
解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/remove-k-digits
关键点和易错点：
（1）首先要思考到的是前缀0的问题，如果字符串前k位有0，那么0之前的字符肯定是要去除的，所以这一步是去判断前面有多少位是确定可以去除的，因为有0，相当于去除了k+1位，当然优先级最高
（2）考虑玩前缀0问题，考虑这情况，431，可以看到3比4小，如果移掉4，3可以继承4的位置，所以整个数比移除其它都小，假设是341，那么应该移除4，因为移除3导致4继承的位置还不如3继续继承自己的位置，而位数都是减1，所以这里有个规律，从左到右，可以遍历入栈方法来做，当下一位的值小于栈顶的值，那么栈顶可以移出去了，让这位小的来继承，否则它也要入栈，这样遍历入栈出栈直到达到要去除的k位数
（3）1,2,两步骤的做法是我提交第一版代码的算法，先考虑前缀后入栈法做的，但提交后突然想到其实步骤1是可以并入到步骤2的，当下一位是0时，可以出栈，然后再判断该0是否需要入栈即可，所以1,2步其实可以合并，代码更简洁
（4）1,2步合并这里有个比较容易发生bug的地方，就是拼接最后结果字符时应该判断栈中有没有元素，如果没有，则应去除未遍历字符前缀的0，如果有，则直接拼接。我之前错在没有判断栈是否有元素就去做去除未遍历字符前缀的0，导致了错误。
第一版提交代码（先做前缀0清除的）：
class Solution(object): def removeKdigits(self, num, k): """ :type num: str :type k: int :rtype: str """ stack = [] zero_flag = 0 tmp = k num_len = len(num) i = 0 while i < num_len: while i < num_len and num[i] == '0': i += 1 zero_flag = i if i < num_len and tmp > 0: tmp -= 1 else: break i += 1 k = i - zero_flag for i in range(zero_flag, num_len): while len(stack) > 0 and i < num_len and int(stack[-1]) > int(num[i]) and k > 0: stack.pop() k -= 1 stack.append(num[i]) if k <= 0: break while k > 0 and len(stack) > 0: stack.pop() k -= 1 result = ''.join(stack) if i+1 < num_len: result += num[i+1:] if result == "": result = "0" return result
第二版优化后的提交代码（1步骤合并到2步骤）：
class Solution(object): def removeKdigits(self, num, k): """ :type num: str :type k: int :rtype: str """ stack = [] num_len = len(num) i = 0 while i < num_len: if k <= 0: break while len(stack) > 0 and int(stack[-1]) > int(num[i]) and k > 0: stack.pop() k -= 1 if num[i] != "0" or (num[i] == "0" and len(stack) > 0): stack.append(num[i]) i += 1 while k > 0 and len(stack) > 0: stack.pop() k -= 1 if len(stack) == 0: while i < num_len and num[i] == "0": i += 1 result = ''.join(stack) if i < num_len: result += num[i:] if result == "": result = "0" return result
16.子数组的最小值之和
给定一个整数数组 A，找到 min(B) 的总和，其中 B 的范围为 A 的每个（连续）子数组。
由于答案可能很大，因此返回答案模 10^9 + 7。
示例：
输入：[3,1,2,4]
输出：17
解释：
子数组为 [3]，[1]，[2]，[4]，[3,1]，[1,2]，[2,4]，[3,1,2]，[1,2,4]，[3,1,2,4]。
最小值为 3，1，2，4，1，1，2，1，1，1，和为 17。
提示：
1 <= A <= 30000
1 <= A[i] <= 30000
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sum-of-subarray-minimums
关键点和易错点：
（1）看错题目了，以为是所有子数组，原来是连续子数组
（2）第一种解法是如果我们知道一个数的前面和后面分别有几个小于它的（等于的情况也需考虑，但只能包含一次，否则就重复计算了，所以代码中是这个数前的包含了，后的没包含），前后个数相乘即为包含这个数的子数组的数目，然后数目乘以这个数大小就是所有连续子数组包含该数且该数是最小情况下的和，其它数类似这样求（这种想法还比较难想，下面这种可能还好想点）
（3）第二种解法是用栈来保持连续性且每前进一个就相当于重组一个子数组，举个例子，比如栈中有3,5，这时下一个如果是6，那么就代表栈中的3,5都会有新子数组如(3,5,6)、（5,6）、(6)，（注意(3,6)是不行的，因为它中间跳过了一个5，它不是连续的），且它们自己是最小的，如果下一个是4，那么就可以弹出大于等于4的，并把count累加到4那里，因为弹出去的可以和新的组成新子数组，栈中的数据和用stack_accumulate变量记录
第一种解法：
class Solution(object): def sumSubarrayMins(self, A): """ :type A: List[int] :rtype: int """ A_len = len(A) pre = [None]*A_len nex = [None]*A_len stack = [] for i in xrange(A_len): while stack and A[i] < A[stack[-1]]: stack.pop() pre[i] = stack[-1] if stack else -1 stack.append(i) stack = [] for i in xrange(A_len-1, -1, -1): while stack and A[i] <= A[stack[-1]]: stack.pop() nex[i] = stack[-1] if stack else A_len stack.append(i) result = 0 MOD = 10**9 + 7 for i in xrange(A_len): result = (result + (i-pre[i])*(nex[i]-i)*A[i]) % MOD return result
第二种解法：
class Solution(object): def sumSubarrayMins(self, A): """ :type A: List[int] :rtype: int """ A_len = len(A) stack_accumulate = 0 total = 0 MOD = 10**9 + 7 stack = [] for item in A: count = 1 while stack and stack[-1][0] >= item: (tmp_val, tmp_count) = stack.pop() count += tmp_count stack_accumulate -= tmp_val * tmp_count stack_accumulate += item * count total += stack_accumulate stack.append((item, count)) return total % MOD
17.表现良好的最长时间段
给你一份工作时间表 hours，上面记录着某一位员工每天的工作小时数。
我们认为当员工一天中的工作小时数大于 8 小时的时候，那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」，意味在这段时间内，「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
示例 1：
输入：hours = [9,9,6,0,6,6,9]
输出：3
解释：最长的表现良好时间段是 [9,9,6]。
提示：
1 <= hours.length <= 10000
0 <= hours[i] <= 16
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-well-performing-interval
关键点和易错点：
（1）要会转变问题，可以把大于8的换为1，小于等于8的换为0，题目就变成经过转换后连续值大于0的最大长度是多少，这一步我想到了，但下一步没想到
（2）然后求出前缀和pre_sum数组，pre_sum[i]代表的含义是在加上第i个前的前缀和，意思就是i之前的数的总和，然后用一个单调递减栈（只记录递减的点，下面的例子递减的点是0，-1，-3）来做，且从后向前遍历，这个想了很久，其实就一个道理，我这里举例说明，假设pre_sum的数组值是0，-1，-3，-2，-1，0，那么用0跟-3比较，0是大于-3的，说明从-3到0之间的这些数字加起来是一定大于0的，所以这个连续段是符合要求的，更新到最大宽度里去。
提交代码：
class Solution(object): def longestWPI(self, hours): """ :type hours: List[int] :rtype: int """ hours_len = len(hours) tran_hours = [None]*hours_len for i in xrange(hours_len): tran_hours[i] = 1 if hours[i] > 8 else -1 pre_sum = [0]*(hours_len+1) for i in xrange(hours_len): pre_sum[i+1] = pre_sum[i] + tran_hours[i] stack = [] for i in xrange(hours_len+1): if not stack or pre_sum[i] < pre_sum[stack[-1]]: stack.append(i) max_len = 0 for i in xrange(hours_len, 0, -1): if i <= max_len: break while stack and pre_sum[i] > pre_sum[stack[-1]]: max_len = max(max_len, i-stack[-1]) stack.pop() return max_len
18.行星碰撞
给定一个整数数组 asteroids，表示在同一行的行星。
对于数组中的每一个元素，其绝对值表示行星的大小，正负表示行星的移动方向（正表示向右移动，负表示向左移动）。每一颗行星以相同的速度移动。
找出碰撞后剩下的所有行星。碰撞规则：两个行星相互碰撞，较小的行星会爆炸。如果两颗行星大小相同，则两颗行星都会爆炸。两颗移动方向相同的行星，永远不会发生碰撞。
示例 1:
输入:
asteroids = [5, 10, -5]
输出: [5, 10]
解释:
10 和 -5 碰撞后只剩下 10。 5 和 10 永远不会发生碰撞。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/asteroid-collision
关键点和易错点：
（1）这道题看起来好像非常简单，但也很容易导致错误，比负数是向左移动的，当栈底没有正数时它应该直接入栈，且之后都不用出栈，因为它不会再发生碰撞了，正数则不管任何条件直接入栈
（2）要处理两者相抵消的情况，即正负数绝对值相等的情况
（3）一定要根据题目找出一些特性，可以简化代码且让逻辑变得清晰，不易出错
提交代码：
class Solution(object): def asteroidCollision(self, asteroids): """ :type asteroids: List[int] :rtype: List[int] """ stack = [] for item in asteroids: if item > 0: stack.append(item) else: add_value = 1 while stack and stack[-1]>0: add_value = stack[-1] + item if add_value == 0: stack.pop() break elif add_value < 0: stack.pop() else: break if add_value != 0 and not (stack and stack[-1] > 0): stack.append(item) return stack
19.迷你语法分析器
给定一个用字符串表示的整数的嵌套列表，实现一个解析它的语法分析器。
列表中的每个元素只可能是整数或整数嵌套列表
提示：你可以假定这些字符串都是格式良好的：
字符串非空
字符串不包含空格
字符串只包含数字0-9, [, - ,, ]
示例 1：
给定 s = "324",
你应该返回一个 NestedInteger 对象，其中只包含整数值 324。
示例 2：
给定 s = "[123,[456,[789]]]",
返回一个 NestedInteger 对象包含一个有两个元素的嵌套列表：
1. 一个 integer 包含值 123
2. 一个包含两个元素的嵌套列表：
i. 一个 integer 包含值 456
ii. 一个包含一个元素的嵌套列表
a. 一个 integer 包含值 789
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/mini-parser
关键点和易错点：
（1）一开始逻辑思路没理清楚，折腾了N久，后面一定要再做一遍，逻辑理清楚了再做
（2）很容易把这包含关系弄反，比如输出是[2,3]的，结果你输出了[3,2]，这是因为栈的特性后进先出误导了你
（3）处理]符号时应该把自己被包含于前一个
（4）要注意[]这个测试案例，最后一步那里的stack长度要判断下，不然这个案例就会错了
提交代码：
# """ # This is the interface that allows for creating nested lists. # You should not implement it, or speculate about its implementation # """ #class NestedInteger(object): # def __init__(self, value=None): # """ # If value is not specified, initializes an empty list. # Otherwise initializes a single integer equal to value. # """ # # def isInteger(self): # """ # @return True if this NestedInteger holds a single integer, rather than a nested list. # :rtype bool # """ # # def add(self, elem): # """ # Set this NestedInteger to hold a nested list and adds a nested integer elem to it. # :rtype void # """ # # def setInteger(self, value): # """ # Set this NestedInteger to hold a single integer equal to value. # :rtype void # """ # # def getInteger(self): # """ # @return the single integer that this NestedInteger holds, if it holds a single integer # Return None if this NestedInteger holds a nested list # :rtype int # """ # # def getList(self): # """ # @return the nested list that this NestedInteger holds, if it holds a nested list # Return None if this NestedInteger holds a single integer # :rtype List[NestedInteger] # """ class Solution(object): def deserialize(self, s): """ :type s: str :rtype: NestedInteger """ stack = [] s_len = len(s) if s[0] != '[': return NestedInteger(int(s)) num, symbol, is_num = 0, 1, False for c in s: if c >= '0' and c <= '9': num = num * 10 + int(c) is_num = True elif c == '-': symbol = -1 elif c == '[': stack.append(NestedInteger()) elif c == ',' or c == ']': if is_num is True: stack[-1].add(NestedInteger(symbol*num)) num, symbol, is_num = 0, 1, False if c == ']' and len(stack) > 1: tmp = stack.pop() stack[-1].add(tmp) return stack[-1]
20.扁平化嵌套列表迭代器
给定一个嵌套的整型列表。设计一个迭代器，使其能够遍历这个整型列表中的所有整数。
列表中的项或者为一个整数，或者是另一个列表。
示例 1:
输入: [[1,1],2,[1,1]]
输出: [1,1,2,1,1]
解释: 通过重复调用 next 直到 hasNext 返回false，next 返回的元素的顺序应该是: [1,1,2,1,1]。
示例 2:
输入: [1,[4,[6]]]
输出: [1,4,6]
解释: 通过重复调用 next 直到 hasNext 返回false，next 返回的元素的顺序应该是: [1,4,6]。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/flatten-nested-list-iterator
关键点和易错点：
（1）说实话很讨厌做这种题目，思维难度本身不高，但老是由于题目给出的接口有时没有说清楚，或细节漏了导致不对
（2）一开始在next里进行迭代，但发现有[]这种案例，会有问题，对于这种应该在has_next里进行迭代判断好点
提交代码：
# """ # This is the interface that allows for creating nested lists. # You should not implement it, or speculate about its implementation # """ #class NestedInteger(object): # def isInteger(self): # """ # @return True if this NestedInteger holds a single integer, rather than a nested list. # :rtype bool # """ # # def getInteger(self): # """ # @return the single integer that this NestedInteger holds, if it holds a single integer # Return None if this NestedInteger holds a nested list # :rtype int # """ # # def getList(self): # """ # @return the nested list that this NestedInteger holds, if it holds a nested list # Return None if this NestedInteger holds a single integer # :rtype List[NestedInteger] # """ class NestedIterator(object): def __init__(self, nestedList): """ Initialize your data structure here. :type nestedList: List[NestedInteger] """ self.stack = [] self.stack.append(nestedList) def next(self): """ :rtype: int """ return self.stack.pop() def hasNext(self): """ :rtype: bool """ while self.stack: tmp_type = type(self.stack[-1]) if tmp_type is int: return True elif tmp_type is list: tmp = self.stack.pop() self.stack.extend(tmp[::-1]) else: tmp = self.stack.pop() if tmp.isInteger(): self.stack.append(tmp.getInteger()) else: tmp_list = tmp.getList() self.stack.extend(tmp_list[::-1]) return False # Your NestedIterator object will be instantiated and called as such: # i, v = NestedIterator(nestedList), [] # while i.hasNext(): v.append(i.next())
21.反转每对括号间的子串
给出一个字符串 s（仅含有小写英文字母和括号）。
请你按照从括号内到外的顺序，逐层反转每对匹配括号中的字符串，并返回最终的结果。
注意，您的结果中 不应 包含任何括号。
示例 1：
输入：s = "(abcd)"
输出："dcba"
示例 2：
输入：s = "(u(love)i)"
输出："iloveu"
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reverse-substrings-between-each-pair-of-parentheses
关键点和易错点：
（1）比较容易想到的一种方法是常规的入栈法，遇到闭括号时，就pop出栈直到遇到开括号，然后反转再append进去，这种方法不易错，而且实现简单，缺点就是做了很多多余的反转，差的情况下可能接近O(n²)
（2）其实我一开始也想到了这样会做很多多余的反转，也联想到了+-数字拆括号那一题，但没想通怎么拆，最后看了别人的思路，原来是反转其实可以从后面append，比如一段字符，abcd，正序那么就从a到d顺序append，那反序不就是d到a这样append吗，然后记住每个括号对应的下标，用分治法递归处理每个括号
简单的入栈法提交代码：
class Solution(object): def reverseParentheses(self, s): """ :type s: str :rtype: str """ stack = [] for c in s: if c == ')': tmp = [] while stack[-1] != '(': tmp.append(stack.pop()) stack.pop() stack.extend(tmp) else: stack.append(c) return ''.join(stack)
分治递归提交代码：
class Solution(object): def reverseParentheses(self, s): """ :type s: str :rtype: str """ s_len = len(s) record_symbol = [None]*s_len stack = [] for i in xrange(s_len): if s[i] == '(': stack.append(i) elif s[i] == ')': pre_symbol = stack.pop() record_symbol[pre_symbol] = i record_symbol[i] = pre_symbol result = [] self.reverse(s, result, 0, s_len-1, record_symbol, True) return ''.join(result) def reverse(self, s, result, begin, end, record_symbol, pos_seq): """ :type s: str :type result: list :type begin: int :type end: int :type pos_seq: bool """ if pos_seq: i = begin while i <= end: if s[i] == '(': self.reverse(s, result, i+1, record_symbol[i]-1, record_symbol, False) i = record_symbol[i] elif s[i] != ')': result.append(s[i]) i += 1 else: i = end while i >= begin: if s[i] == ')': self.reverse(s, result, record_symbol[i]+1, i-1, record_symbol, True) i = record_symbol[i] elif s[i] != '(': result.append(s[i]) i -= 1
22.最大频率栈
实现 FreqStack，模拟类似栈的数据结构的操作的一个类。
FreqStack 有两个函数：
push(int x)，将整数 x 推入栈中。
pop()，它移除并返回栈中出现最频繁的元素。
如果最频繁的元素不只一个，则移除并返回最接近栈顶的元素。
示例：
输入：
["FreqStack","push","push","push","push","push","push","pop","pop","pop","pop"],
[[],[5],[7],[5],[7],[4],[5],[],[],[],[]]
输出：[null,null,null,null,null,null,null,5,7,5,4]
解释：
执行六次 .push 操作后，栈自底向上为 [5,7,5,7,4,5]。然后：
pop() -> 返回 5，因为 5 是出现频率最高的。
栈变成 [5,7,5,7,4]。
pop() -> 返回 7，因为 5 和 7 都是频率最高的，但 7 最接近栈顶。
栈变成 [5,7,5,4]。
pop() -> 返回 5 。
栈变成 [5,7,4]。
pop() -> 返回 4 。
栈变成 [5,7]。
提示：
对 FreqStack.push(int x) 的调用中 0 <= x <= 10^9。
如果栈的元素数目为零，则保证不会调用 FreqStack.pop()。
单个测试样例中，对 FreqStack.push 的总调用次数不会超过 10000。
单个测试样例中，对 FreqStack.pop 的总调用次数不会超过 10000。
所有测试样例中，对 FreqStack.push 和 FreqStack.pop 的总调用次数不会超过 150000。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-frequency-stack
关键点和易错点：
（1）没有联想到要使用map来做，但对于这种较复杂的一般都需要借助map来帮助简化算法实现
（2）知道可以使用map后，并没有马上想到思路，还是琢磨了段时间才想出，数据结构组织不够灵敏
（3）思想就是一个dict用来记录出现的数值和对应的次数，一个dict用来记录次数对应一个列表，比如我这个数是5，前面已经进来2个5了，所以我是第3个5，我就放到3对应的表上，append进去（其实这里我想到了操作系统里的根据进程优先级来做的思想，类似于链表，某个优先级的进程都链接在这个链表上）
提交代码：
class FreqStack(object): def __init__(self): self.map_to_count = {} self.map_to_list = {} self.cur_max = 0 def push(self, x): """ :type x: int :rtype: None """ if x in self.map_to_count: self.map_to_count[x] += 1 else: self.map_to_count[x] = 1 if self.map_to_count[x] <= self.cur_max: self.map_to_list[self.map_to_count[x]].append(x) else: self.cur_max += 1 self.map_to_list[self.cur_max] = [x] def pop(self): """ :rtype: int """ cur_max_num = self.map_to_list[self.cur_max].pop() if not len(self.map_to_list[self.cur_max]): self.cur_max -= 1 self.map_to_count[cur_max_num] -= 1 return cur_max_num # Your FreqStack object will be instantiated and called as such: # obj = FreqStack() # obj.push(x) # param_2 = obj.pop()
23.索引处的解码字符串
给定一个编码字符串 S。为了找出解码字符串并将其写入磁带，从编码字符串中每次读取一个字符，并采取以下步骤：
如果所读的字符是字母，则将该字母写在磁带上。
如果所读的字符是数字（例如 d），则整个当前磁带总共会被重复写 d-1 次。
现在，对于给定的编码字符串 S 和索引 K，查找并返回解码字符串中的第 K 个字母。
示例 1：
输入：S = "leet2code3", K = 10
输出："o"
解释：
解码后的字符串为 "leetleetcodeleetleetcodeleetleetcode"。
字符串中的第 10 个字母是 "o"。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/decoded-string-at-index
关键点和易错点：
（1）一开始的思路都是往着模拟进行在思考，所以一直也想不出，固定性思维需要打破
（2）对于字符串的题目应该要学学反向思维，从后往前推
（3）最后那里的取模也很关键，很精髓
提交代码：
class Solution(object): def decodeAtIndex(self, S, K): """ :type S: str :type K: int :rtype: str """ s_len = len(S) char_all_count = 0 for c in S: if c.isalpha(): char_all_count += 1 else: char_all_count *= (int(c)) for i in xrange(s_len-1, -1, -1): K %= char_all_count if K == 0 and S[i].isalpha(): return S[i] if S[i].isalpha(): char_all_count -= 1 else: char_all_count /= int(S[i])
24.奇偶跳
给定一个整数数组 A，你可以从某一起始索引出发，跳跃一定次数。在你跳跃的过程中，第 1、3、5... 次跳跃称为奇数跳跃，而第 2、4、6... 次跳跃称为偶数跳跃。
你可以按以下方式从索引 i 向后跳转到索引 j（其中 i < j）：
在进行奇数跳跃时（如，第 1，3，5... 次跳跃），你将会跳到索引 j，使得 A[i] <= A[j]，A[j] 是可能的最小值。如果存在多个这样的索引 j，你只能跳到满足要求的最小索引 j 上。
在进行偶数跳跃时（如，第 2，4，6... 次跳跃），你将会跳到索引 j，使得 A[i] => A[j]，A[j] 是可能的最大值。如果存在多个这样的索引 j，你只能跳到满足要求的最小索引 j 上。
（对于某些索引 i，可能无法进行合乎要求的跳跃。）
如果从某一索引开始跳跃一定次数（可能是 0 次或多次），就可以到达数组的末尾（索引 A.length - 1），那么该索引就会被认为是好的起始索引。
返回好的起始索引的数量。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/odd-even-jump
关键点和易错点：
（1）这道题有思路且思路跟官方差不多但自己写出来的代码太过繁杂
（2）思路就是类似于打表，从后往前，假设知道了index=j的偶数跳跃是可以到达或者不能到达最后一个数的，那么当i这个数经过第一次的奇数跳跃如果跳到了index=j，那么直接用j的偶数跳跃能否到达来判断即可，所以其实就是维护这些从后到前的跳跃能否到达最后一个数的值
（3）还有个是要找出奇数跳跃和偶数跳跃会跳到哪个index，这个想了挺久没想到，官方其实是先排了个序然后用栈（排序为栈构造了有序的特性）计算了每个数的下一个奇数和下一个偶数的列表，挺精髓的
提交代码：
class Solution(object): def oddEvenJumps(self, A): """ :type A: List[int] :rtype: int """ A_len = len(A) def build_next_arr(B): stack = [] tmp_next = [None]*A_len for i in B: while stack and i > stack[-1]: tmp_next[stack.pop()] = i stack.append(i) return tmp_next B = sorted(range(A_len), key=lambda x: A[x]) odd_next = build_next_arr(B) B.sort(key=lambda x: -A[x]) even_next = build_next_arr(B) odd_jump = [False]*A_len even_jump = [False]*A_len odd_jump[A_len-1] = True even_jump[A_len-1] = True for i in xrange(A_len-2, -1, -1): if odd_next[i] is not None: odd_jump[i] = even_jump[odd_next[i]] if even_next[i] is not None: even_jump[i] = odd_jump[even_next[i]] return sum(odd_jump)
