DES加密算法解析与实现
DES对称加密算法详解
DES简介
DES全称为Data Encryption
Standard,即数据加密标准,是一种使用密钥加密的块算法,1977年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),并授权在非密级政府通信中使用,随后该算法在国际上广泛流传开来。需要注意的是,在某些文献中,作为算法的DES称为数据加密算法(Data Encryption Algorithm,DEA),已与作为标准的DES区分开来。
DES算法就是一个把64位的明文输入块变为64位密文输出块的算法,它所使用的密钥也是64位(其实只使用到了56位,其余8位为奇偶校验位)
DES算法的入口参数有三个:Key、Data、Mode。
> Key(密钥):为7个字节共56位,是DES算法的工作密钥(若说密钥为64位,其指的也是56位的秘钥加上8位奇偶校验位,奇偶校验位为第8,16,24,32,40,48,56,64位)
> Data(数据):为8个字节64位,是要被加密或被解密的数据
> Mode(模式): 为DES的工作方式,有两种:加密或解密。
算法特点:分组比较短、密钥太短、密码生命周期短、运算速度较慢。
Unicode码
Unicode只有一个字符集,中、日、韩的三种文字占用了Unicode中0x3000到0x9FFF的部分
Unicode目前普遍采用的是UCS-2,它用两个字节来编码一个字符,比如汉字"经"的编码是0x7ECF,注意字符码一般用十六进制来表示,为了与十进制区分,十六进制以0x开头,0x7ECF转换成十进制就是32463,UCS-2用两个字节来编码字符,两个字节就是16位二进制,2的16次方等于65536,所以UCS-2最多能编码65536个字符。编码从0到127的字符与ASCII编码的字符一样,比如字母"a"的Unicode编码是0x0061,十进制是97,而"a"的ASCII编码是0x61,十进制也是97,对于汉字的编码,事实上Unicode对汉字支持不怎么好,这也是没办法的,简体和繁体总共有六七万个汉字,而UCS-2最多能表示65536个,才六万多个,所以Unicode只能排除一些几乎不用的汉字,好在常用的简体汉字也不过七千多个,为了能表示所有汉字,Unicode也有UCS-4规范,就是用4个字节来编码字符。
DES算法整体流程
DES算法整体流程
DES算法的流程图在网上很容易找到,我们使用下图为例,并配上我们的解析:
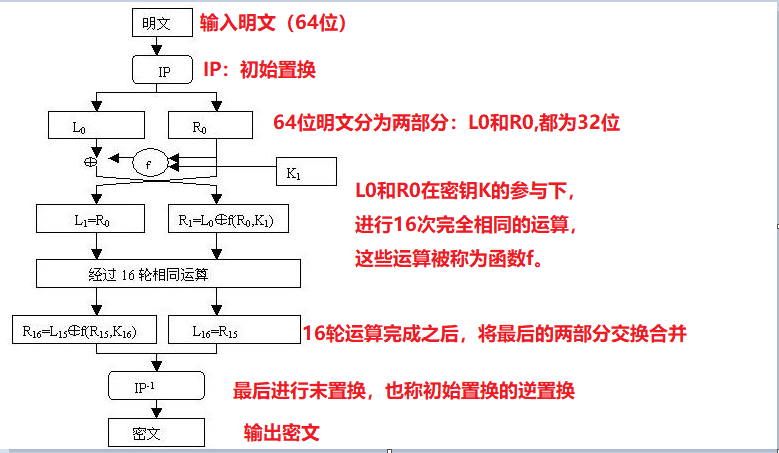
通过上面的流程图,相信大家就可以大致了解了DES加密算法的流程。
我们可以转化为文字:
一开始输入64位的明文数据;
然后进行初始置换(IP);
初始置换之后,将生成的64位数据分为左右两部分,每部分为32位,命名为L0(Left0)、R0(Right0);
然后这两部分在密钥k的参与下,根据函数f进行16轮完全相同的运算,我们称为16轮迭代运算,每运算一次,左右两部分的命名就改变一次,比如第一轮运算后,L0、R0就变为L1、R1,直到16论运算完成,L0变为L16,R0变为R16;
在16轮运算完成之后,将L16和R16交换,并且合并为64位;再经过末置换(初始置换的逆置换/终止置换),输出密文。
应该注意的是,我们上面说到的16轮完全相同的运算,指的是运算所使用的函数或者说算法是一样的,但是参数L、R以及K是不相同的,L、R不用多说,就是上次运算所得的L和R,但每一轮参与运算的K是我们的入口参数Key,经过某个特定的交换规则交换后,生成16个子秘钥,我们命名为K1,K2,K3….K16。
函数f的大致流程
上面我们提到,经过初始置换后,会进行16轮相同的运算,现在我们简单介绍一下这个运算函数中,都进行了哪些运算,运算的主要流程图如下:

从上图我们可以知道,函数f主要对数据的右半部分R进行了操作,
1. 先对其进行扩展置换,使其变为48位的数据,
2. 然后生成的数据再与子密钥进行异或运算,得到一组新的48位数据
3. 再以异或运算后的48位数据进行S盒代替,将48位的数据,转换为32位的数据,
4. 再进行P盒置换,生成32位的数据
5. 最后将P盒置换生成的数据与本轮运算时输入的的L进行异或运算,生成新的R。
6. 而新的L是直接由本轮的R进行替换
DES加密实现细节
IP置换(初始置换)实现细节
初始置换的原理其实很简单,根据一个初始置换表,对照表中的数值,将明文数据相应位置的数据移动到该数据所在的位置即可,初始置换表如下:
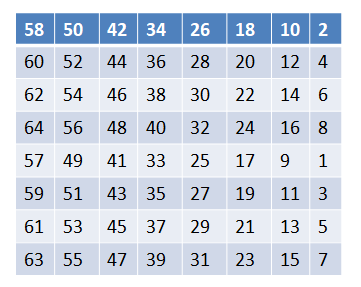
从上表我们可以总结出,初始置换表的规律其实就是(其实不用太在意这个规律):
1.偶数与奇数分开(1\~64),然后分为上下两部分,分布在置换表中,偶数在上,奇数在下。
2. 在偶数与奇数内部,又遵从“从右到左,从上到下,从小到大”的排列。
由于二进制数据不容易看到置换后的改变,我们这里展示初始置换的流程时,不使用实际加密中的二进制数据,而是用字母代替,如下:
我们要进行置换的内容为:"abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+="
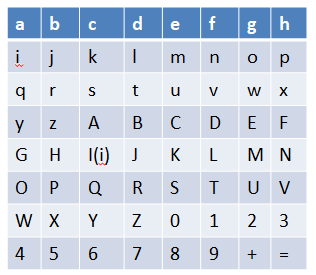
我们这样理解,a就是加密的64位数据中的第一位,b就是第二位,依次类推,那么,初始置换的过程就应该是这样的:
第一步,先置换a:
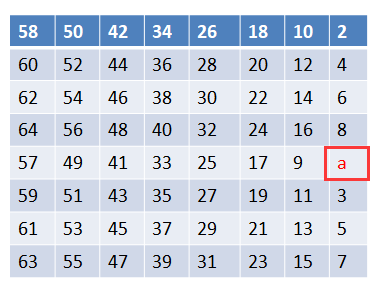
然后置换b:
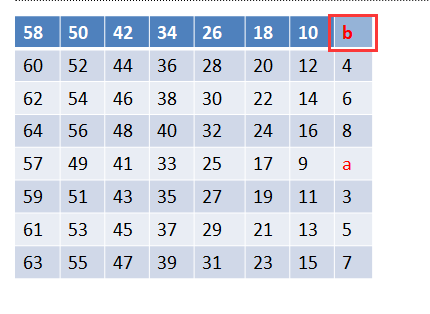
直到置换完最后一位:
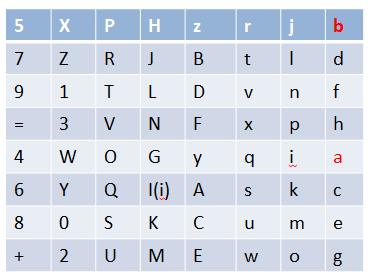
至此我们便得到了初始置换之后的数据
Data=“5XPHzrjb7ZRJBtld91TLDvnf=3VNFxph4WOGyqia6YQI(i)Askc80SKCume+2UMEwog”
从前面任务中DES加密算法的整体流程知道,初始置换完成之后,就需要将置换后的数据分为L0、R0:
L0 = “5XPHzrjb7ZRJBtld91TLDvnf=3VNFxph”
R0 = “4WOGyqia6YQI(i)Askc80SKCume+2UMEwog”
函数f实现细节
初始置换之后,就是我们的16轮运算,我们需要知道的是运算函数f,以及在运算过程中数据与密钥如何结合。
f函数作用于每轮的K(子密钥)值和每轮的待加密文本的右半部分(R)。//我们后面出现的K0、R0等等,字母后面有数字的,都是代表对应轮数运算中的K、R等。
从我们前面的函数f流程图,我们可以清晰的了解到,经过一轮运算之后,新的L是原来的R直接赋值的,即:L1=R0,新的R是原来的L与经过f函数处理的原R进行异或运算后得到的(R1=L0^f(R0,K1))。
那么我们现在需要了解的就是这么几个问题:
1. 子秘钥K(1\~16)是如何得到的
2. 扩展置换的流程是如何的,其后的异或运算又是怎样的
3. S盒替换是如何替换的
4. P盒置换又是如何操作的
子秘钥K
子秘钥K的生成过程中,又有两次置换,称为压缩置换1和压缩置换2,大致流程图如下:
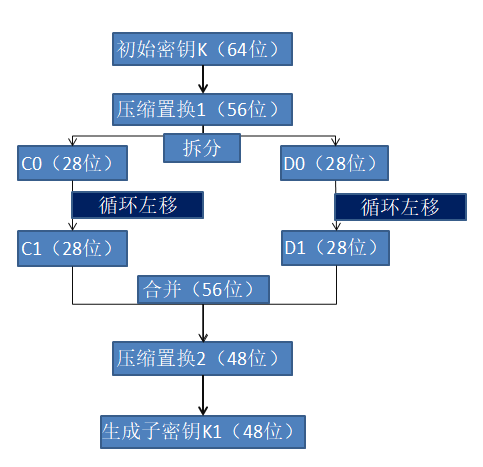
从流程图我们可以清楚的知道:
1. 初始密钥在经过第一次压缩置换之后,生成56位数据,
2. 再将这56位数据从中间拆分开来,命名为C0,D0,都是28位数据
3. 然后根据正在运算的轮数,将数据左移相应的位数,来得到C1和D1,
4. 最后,压缩置换1未完成,将C1,D1合并为56位的数据,
5. 经过压缩置换2之后,生成子密钥K1,即生成了第一轮运算时使用的子密钥。
接下来的每一轮运算中的子密钥K都是由上一轮生成的子密钥经过这两次压缩置换得到的。不同的地方在于C和D循环左移的位数,在每一轮中都是不同的。具体的对应表如下(即C1、D1是由C0、D0移位得到,C2、D2是由C1、D1移位得到……..以此类推):

那么好,了解主要流程之后,我们再举例子,为了直观一点,我们还是使用“abc…..”来代替二进制的“0101”:
假设我们现在的初始秘钥是8个字节,也就是64位:
“abcdefgh ijklmnop qrstuvwx yzABCDEF GHIJKLMN OPQRSTUV WXYZ0123 456789+=”
压缩置换1
我们将64位数据分成8组,每一组的最后一位数据,是奇偶校验位,虽然也属于密钥,但是不参与加密运算,也就是去掉这些标红的数据,剩下的56位数据就是需要参与到压缩置换1的数据,如下图:
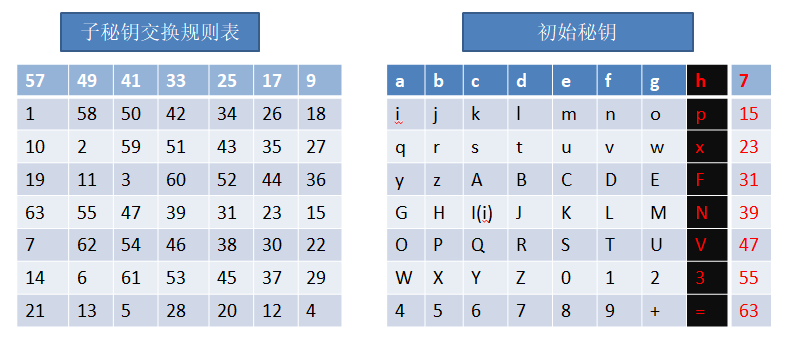
跟之前讲过的初始置换一样,将字母换到对应的位置上就可以了(为了方便我们在初始秘钥的表格后面标注了每行最后一个参与置换的字母的位置,比如g是第7位,o是第15位),置换完成后:
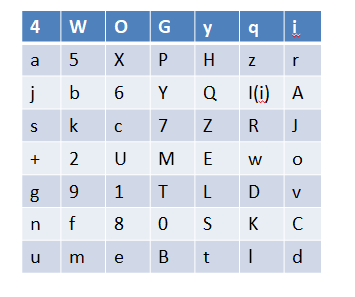
那么经过这次置换呢,我们可以总结出压缩置换1的规律:
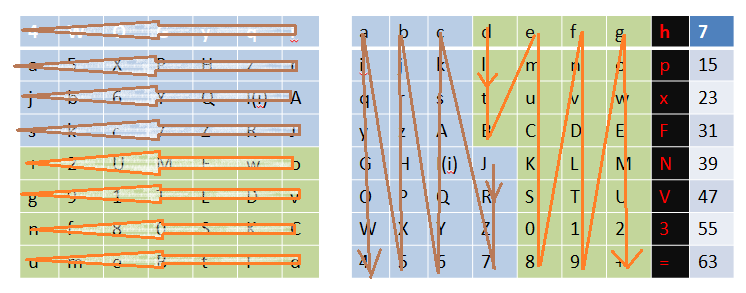
就是将56位的数据从按照我们所标识的颜色来分成两组,然后按照我们上图所示的顺序排列。
经过压缩置换1之后,我们就得到一个K0,再将这个K0拆分,得到C0、D0,进而得到C1、D1,最后得到K1。
压缩置换1接下来的是拆分:
K0 = “4WOGyqia5XPHzrjb6YQI(i)Askc7ZRJ+2UMEwog91TLDvnf80SKCumeBtld”
C0 = “4WOGyqia5XPHzrjb6YQI(i)Askc7ZRJ”
D0 = “+2UMEwog91TLDvnf80SKCumeBtld”
拆分之后我们得到C0、D0,再然后就是循环左移,求出C1、D1:
我们根据“轮数与左移位数”的对应表,得知,我们现在要求的是C1、D1,也就是第一轮运算,那么循环左移的位数就是1位,就可以得到:
C1 = “WOGyqia5XPHzrjb6YQI(i)Askc7ZRJ4”
D1 = “2UMEwog91TLDvnf80SKCumeBtld+”
如上,左移的同时还要保持位数不变,所以最前面(左侧)移动的数据又补充到后面。然后将C1D1合并:
C1D1 = “WOGyqia5XPHzrjb6YQI(i)Askc7ZRJ42UMEwog91TLDvnf80SKCumeBtld+”
放在表格中(黑色表格中的是每一行最后一位的位数):
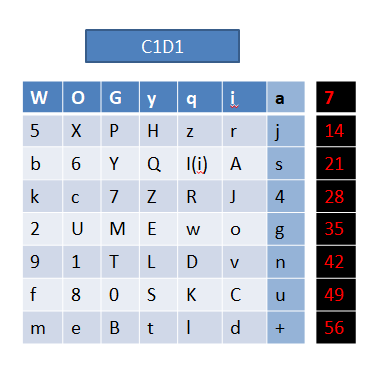
压缩置换2
要得到子秘钥K1,还需要进行压缩置换2,经过压缩置换2之后56位的C1D1被压缩成48位的K1:
压缩置换2遵循的规则表如下:
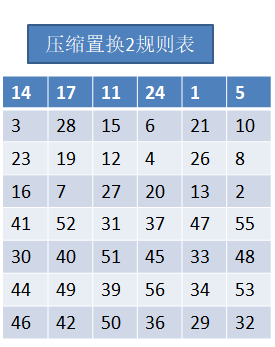
得到K1:

> K1 = “jYH7WqG4bisPcI(i)zyR56aJArOvBM1KdUDe0wC8uL+otSnm92E”
至此我们便得到了第一轮真正的子密钥:K1
扩展置换E
接下来我们了解扩展置换E的细节:
扩展置换的作用对象是我们在初始置换后,将数据拆分为两部分(L,R)中的右半部分R。
扩展置换表如下:
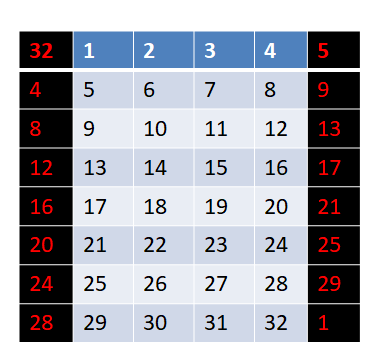
可能不太好理解,我们用文字描述一下,就是将数据R(32位),按照每4位一组,拆分成8个组,如图,左右两侧黑色的两列是扩展时添加的数据,中间的就是分组后的数据R,表中的数字代表数据R中的位置。分成8组织后,遵循这样的一个规则:
1. 每一组的头部添加本组数据上一组的尾部,
2. 每一组的尾部添加本组数据下一组的头部。
即第一组数据,前面添加的是最后一组的最后一位数据,后面添加的是第二组的第一位数据…以此类推,
如果还不懂,那么我再插一个图:
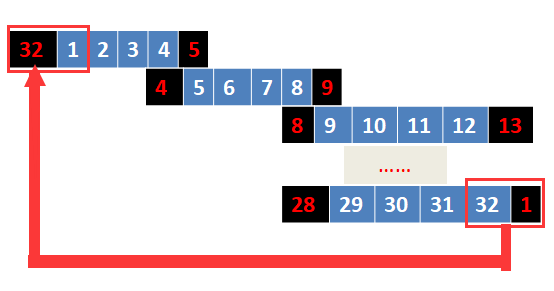
好了,现在拿我们上面得到的R0进行扩展置换:
先分组:
R0 = “4WOGyqia6YQI(i)Askc80SKCume+2UMEwog”
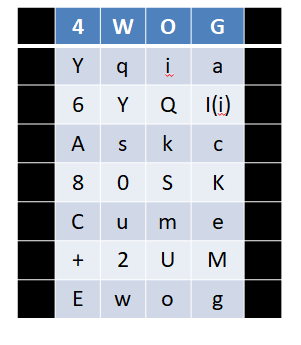
然后进行扩展:
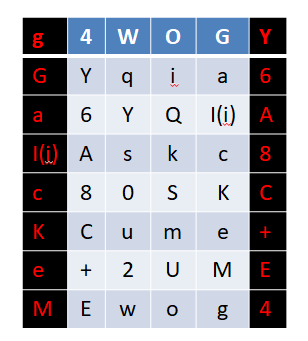
之后我们便得到了扩展到48位的R0:
R0=“g4WOGYGYqia6a6YQI(i)AI(i)Askc8c80SKCKCume+e+2UMEMEwog4”
扩展置换E结束之后,我们要进行的就是K1与R0的异或运算,由于我们这里不是采用的真正的二进制数据,所以我们不做此步骤的详细解释,毕竟只是一个异或运算,很简单。
S盒代替
S盒代替的作用,就是将我们上一步,R0与K1异或后得到的48位数据压缩为32位数据。
S盒一共有8个,每一个都是一个4行16列的数组,具体如下:

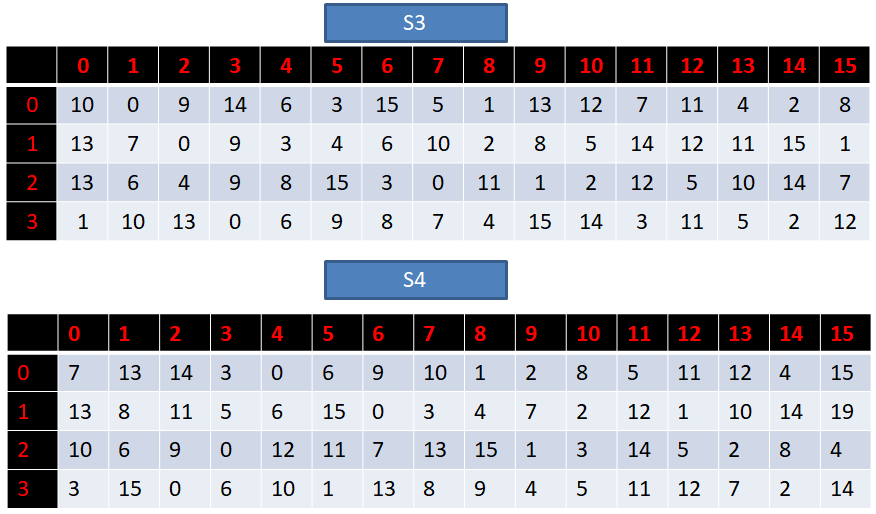
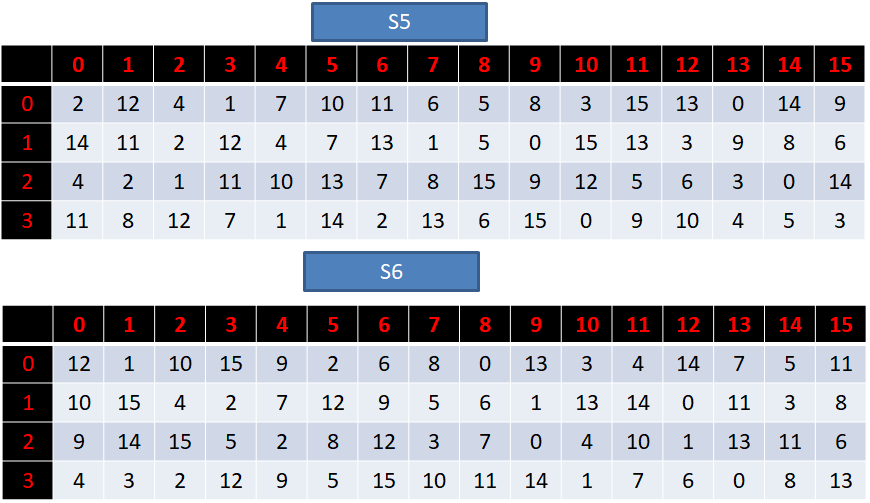
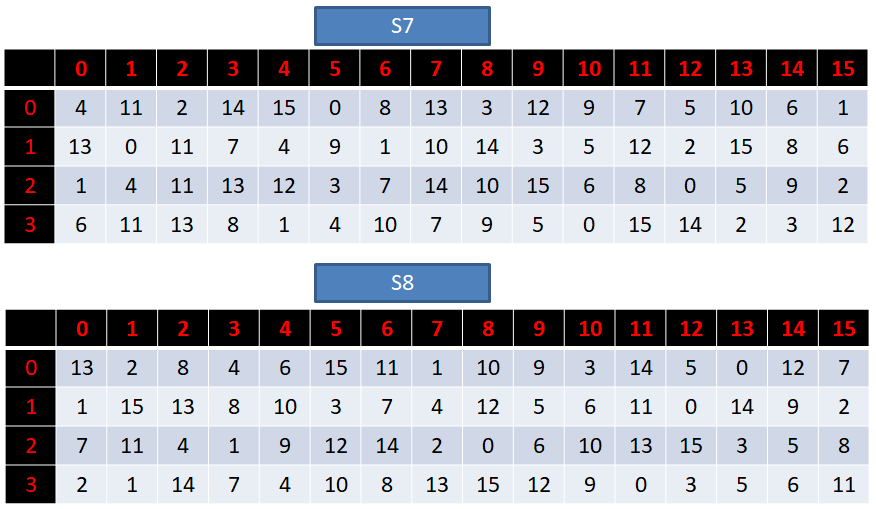
接下来我们讲解一下S盒代替的过程:
1. 我们前面扩展置换后得到的R0是48位的数据,我们的S盒有8个,那么我们就需要将得到的R0平均分为8组,每组对应一个S盒。
2. 每一组的数据长度为6位,假设第一组的二进制数据为:“100110”
3. 那么,我们取第一位与最后一位,组成十进制行数:“10”=2
4. 然后取中间四位,组成十进制列数:“0011”=3
5. 那么,在对应的S1盒中,取2行3列的数据(第3行第4列):8
6. 再将取得的数字转换为2进制:“1000”
7. 将这个得到的4位二进制数据,代替原来第一组的6位数据,这样一来,等8个S盒全部代替完毕,我们就得到32位的数据。
P盒置换
S盒置换完成之后,要进行的就是P盒置换了,输入32位的数据,得到32位的输出。置换表以及置换举例如下:

至此我们便得到了f(R0,K1),只要再与L0进行异或运算,就得到了第一轮运算最终的R1,然后再将R0的值赋给L1,就完成了第一轮的运算,得到了L1,R1。
末置换(也称初始置换的逆置换/终止置换)
经过16次的运算,我们在函数f的最后,会得到“L16、R16”,这正是我们需要的,然后将L16与R16合并,但是与之前的步骤中的合并不同,此次合并需要先交换二者的位置,也就是应该是R16L16。
合并之后我们就得到了长度为64位的数据,在用这64位数据进行终止置换,最终得到的数据就是加密后的数据。
终止置换表如下(我们不再举例,反正都一样):
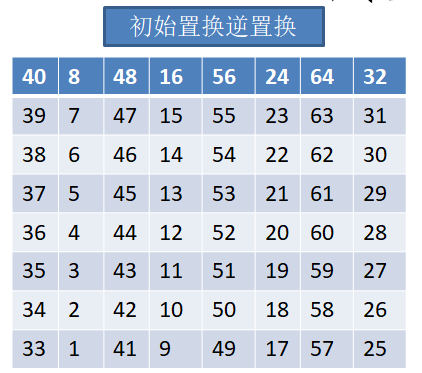
Python实现
我们只是用python实现以下简单的加密步骤,我们在此次试验中不考虑的情况有这些:
1. 需要加密的文本超过64位或者不足64位怎么办?
2. 加密后的文本如何显示(这涉及到编码问题),我们的代码运行完成之后是直接显示最后加密完成的二进制数据
3. 用户输入的秘钥超出64位长度或者不足64位长度怎么办?
4. 得到一串密文应该如何解密(这也涉及到编码的问题),也就是我们的代码只实现加密的过程,不实现解密的过程
也就是利用python,将加密的细节展示出来.
我们首先要把加密过程中需要用到的置换表都准备好:
初始置换表与终止置换表:
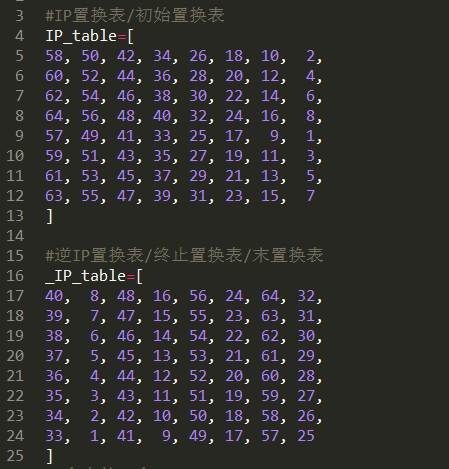
8个S盒:
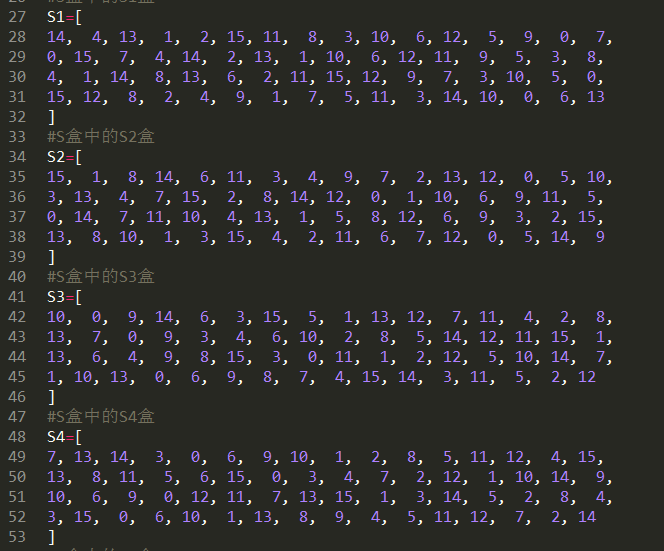
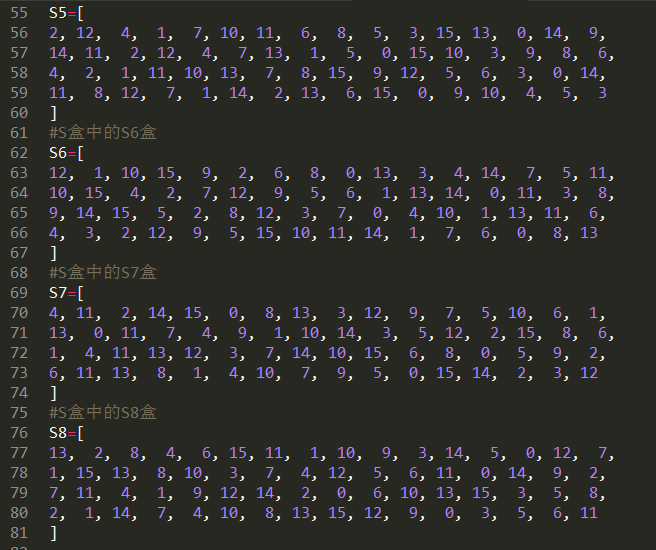
P盒

压缩置换表
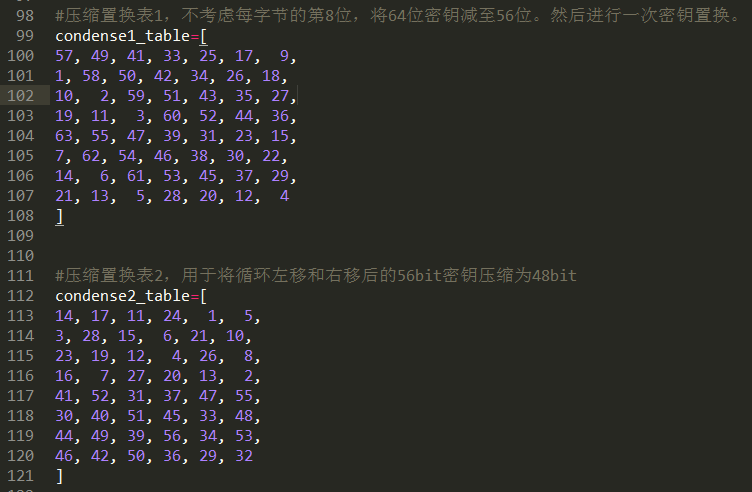
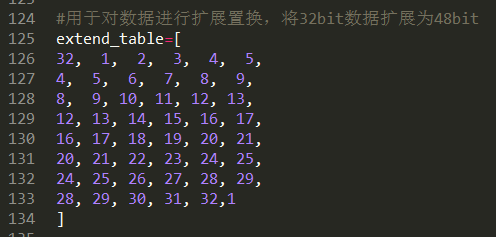
扩展置换表
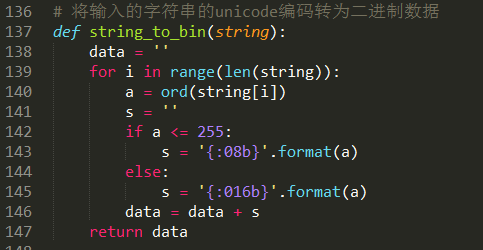
我们知道,无论是要加密的文本,还是密钥,在加密的过程中都是以二进制的形式被处理的,所以我们需要一个函数来对所有输入的字符串进行处理,将其转换为二进制,我们直接使用ord函数将输入的数据转换为其对应的unicode编码的十进制,再转换为二进制,因为python的bin函数转换成的二进制会自动删除高位的0,所以我们使用“{:08b}.format()”这样的方式来使生成的二进制保持一定的位数:
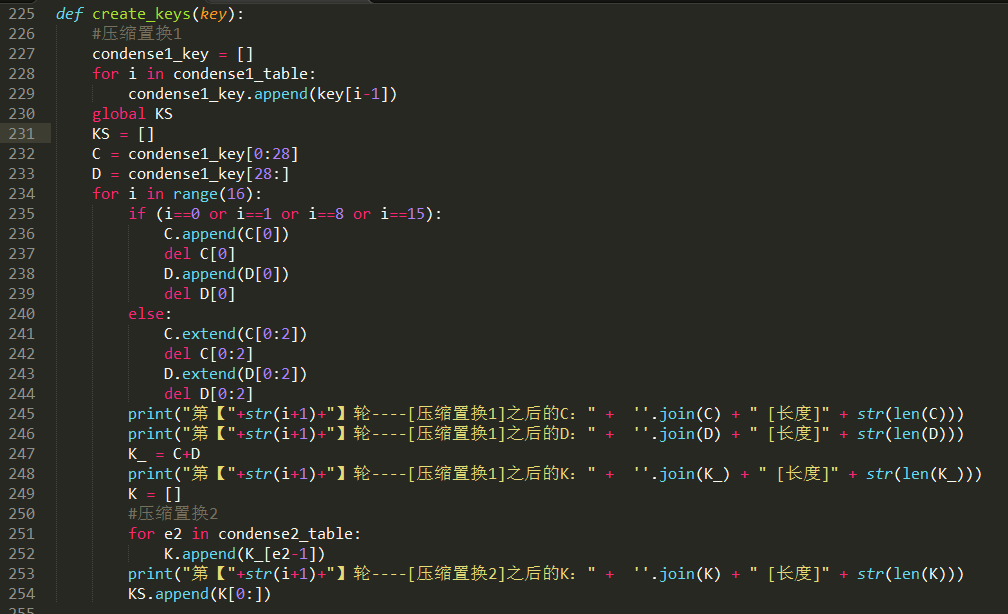
我们先将子密钥的生成搞出来,如下图,我们创建子秘钥生成的函数,所需参数为初始密钥的二进制文本,根据前面的原理知识,进行压缩置换之后,分为C、D两部分,然后进行移位,一口气完成16次的移位之后,将生成的子密钥全部保存在全局列表KS中,方便之后的加密函数调用这些子密钥:
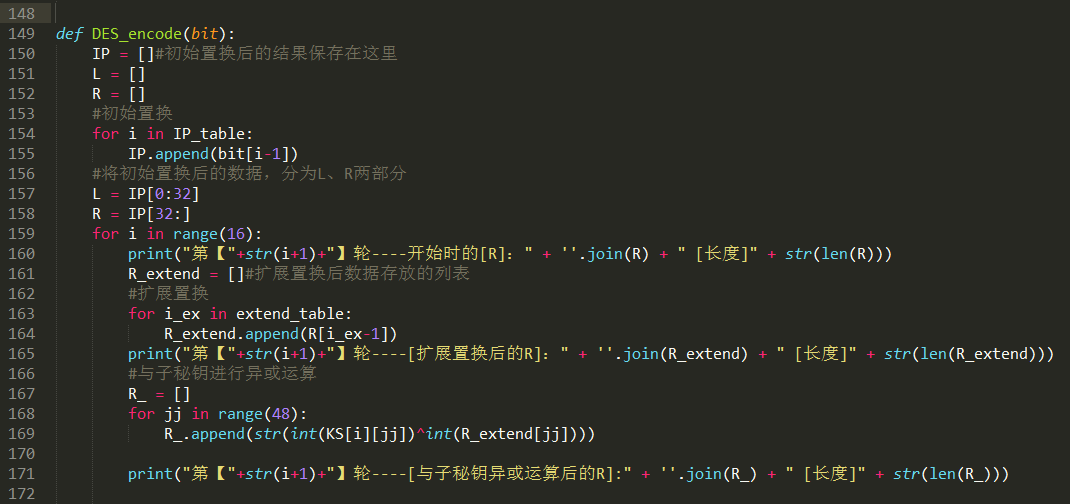
加密函数,就不在这里细说了,看代码中的注释就可以理解了呢。
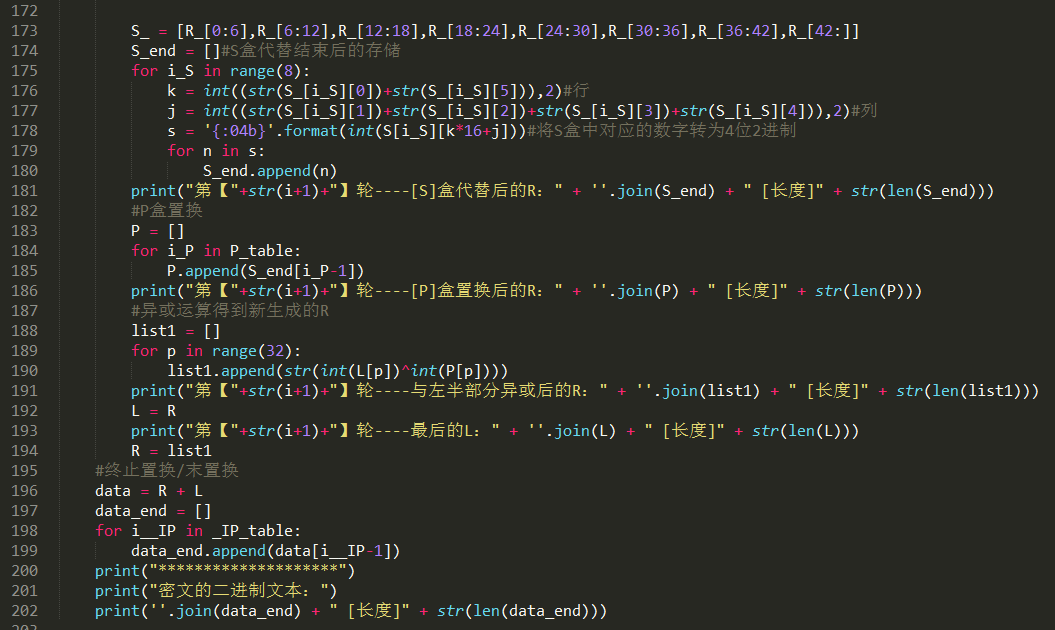

执行脚本,对字符串“testtest”进行加密,秘钥为“12345678”:
等待加密完成:
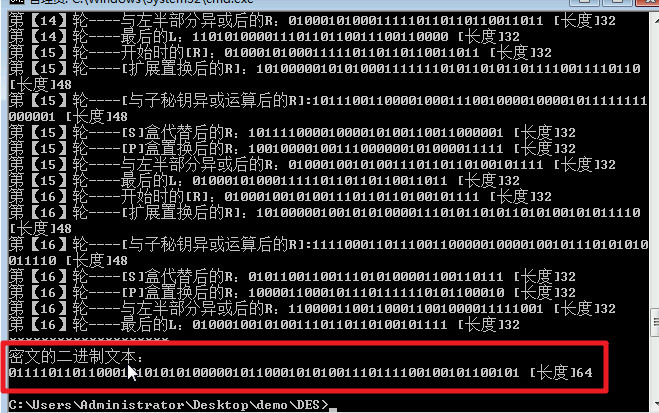
参考文章
https://blog.csdn.net/m0_37962600/article/details/79912654
https://blog.csdn.net/u013005150/article/details/25804787
https://www.bilibili.com/video/av18027475?from=search&seid=10214518854180201048



 浙公网安备 33010602011771号
浙公网安备 33010602011771号