二维码之QR码生成原理与损坏修复

目录

• 二维码基础知识
• QR 码的格式与生成原理
  • QR码的尺寸
  • QR码的格式
    • 定位图案
    • 格式信息
    • 版本信息
    • 数据码字和纠错码字
  • 数据编码与编码流程
    • QR码支持的数据编码
    • 示例一：
    • 示例二：
    • 结束符和补齐符
    • 纠错码
    • Remainder Bits（剩余位）
  • 掩码（也叫掩模）
• 手绘二维码
  • 准备固定格式的填充模板
  • 进行数据编码
  • 计算纠错码
  • 码字整理
  • 数据填充
  • 与掩码进行异或运算
  • 手绘完成
• MMA2015-MISC400-qr二维码恢复挑战
  • 题目分析
  • 获取格式信息
  • 获取原始码字
  • 尽可能多地恢复数据
  • 编写脚本恢复
  • 拆分和解码
• 二维码恢复挑战-二维码恢复工具
  • 题目分析
  • 整理已知信息
  • 恢复初始数据
  • 读取数据码字
  • 整理信息
  • 脚本读取
  • 使用工具恢复
• 参考文章

二维码基础知识

一提到二维码，我们就会想起生活中处处都能见到的“二维码”，比如收款码、付款码、微信名片等等。但是严格意义来讲，这些码只是众多二维码中的一种，叫做QR码，也是现在我们使用最广泛的一种二维码。

二维码又称二维条码，是用某种特定的几何图形按一定规律在平面（二维方向上）分布的、黑白相间的、记录数据符号信息的图形；在代码编制上巧妙地利用构成计算机内部逻辑基础的“0”、“1”比特流的概念，使用若干个与二进制相对应的几何形体来表示文字数值信息，通过图象输入设备或光电扫描设备自动识读以实现信息自动处理：它具有条码技术的一些共性：每种码制有其特定的字符集；每个字符占有一定的宽度；具有一定的校验功能等。同时还具有对不同行的信息自动识别功能、及处理图形旋转变化点。

二维码的种类有很多，除了我们常见的QR码外，使用比较广泛的还有：PDF417、DM、汉信码等。有兴趣的可以自行查阅

QR 码的格式与生成原理

QR码的尺寸

首先，我们先说一下QR码一共有40种尺寸。官方叫做版本Version(版本)。
Version 1是21x21的矩阵；
Version 2是25x25的矩阵；
Version 3是29x29的矩阵...
每增加一个version，就会增加4的尺寸（或者称单位，看后面就会理解），公式是：(V-1)*4 + 21（V是版本号） 最高Version 40，(40-1)*4+21 = 177，所以最高是177 x 177的正方形。
鉴于大家平时都已经习惯称呼QR码为二维码，我们后面的内容也就不一直强调QR码，而是称为二维码。大家只要明白，我们后面所说的二维码，都是指QR码即可。

QR码的格式

QR码格式示例如下：
英文版：

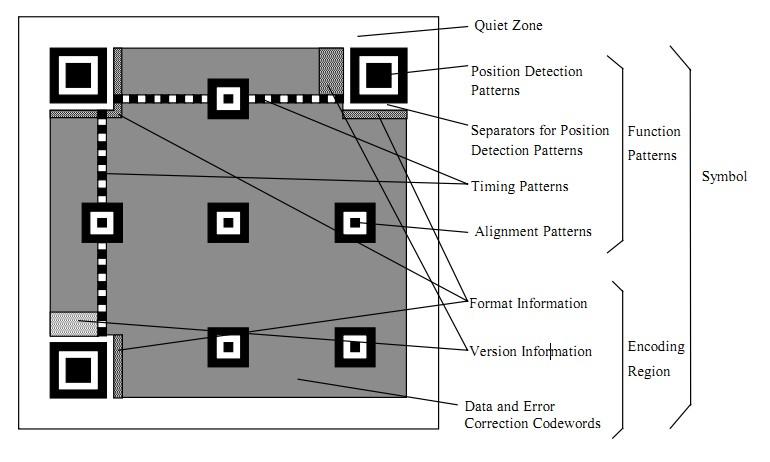
中文版：

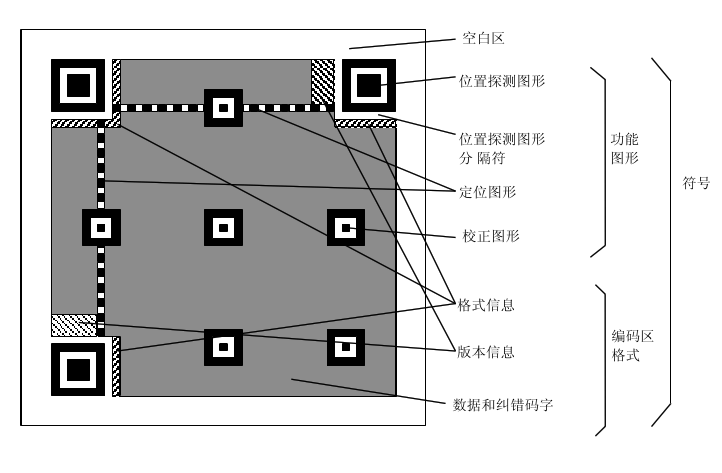
定位图案

Position Detection Pattern（位置探测图形）是定位图案的一种，就是每个二维码都有的左上、左下和右上三个角的“回”字形的标志。用于标记二维码的矩形大小。这三个定位图案有白边叫Separators for Postion Detection Patterns。之所以三个而不是四个，因为三个就足以标识一个矩形了，用四个反而多余，且会使得能够表示的数据空间变小，扫描器在进行二维码扫描的时候会根据这三个定位标识符来更正二维码的坐标，方便进行扫描。这块区域的尺寸固定，无论是哪个版本的二维码，他的尺寸都是7*7的模块。

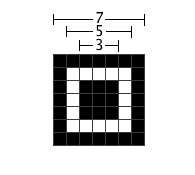
Alignment Patterns（校正图形） 只有在Version 2以上（包括Version2）的二维码中需要这个东西，同样是为了定位用的。它的尺寸也是固定的，为5*5的模块。

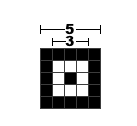
Timing Patterns（定位图形）也是用于定位的，是一单位宽的黑白交替点带，由黑色点起始和结束。原因是二维码有40种尺寸，尺寸过大了后需要有根标准线，不然扫描的时候可能会扫歪了。

格式信息

Format Information 存在于所有的版本中，用于存放一些格式化数据的，通过读取这部分的内容，可以知道当前二维码的纠错等级、掩码类别。主要内容为“纠错等级（2bit）+ 掩码类别（3bit）+ BCH code(10bit,用于纠错)”，然后这15个bits还要与101010000010010做XOR操作，主要是为了如果选用了00的纠错级别和000的Mask，从而造成全部为白色，这会增加扫描器的图像识别的困难。
纠错等级的比特表示：

为了增强二维码的容错能力，保证在一定的损坏范围内，不会影响数据的读取，共设计了两个区域来存放两条一模一样的格式信息。
这15个bit在format information区域内的分布以及顺序如下（下图中数字的顺序就是这15个bit的存放顺序，应当注意的是这些数字表示的是位的高低，也就是当获取到格式信息15个bit长度的二进制字符串时，左边为高位，右边为低位，所以最左侧的二进制数字应该在14的位置，最右侧的二进制数字应该在0的位置）：

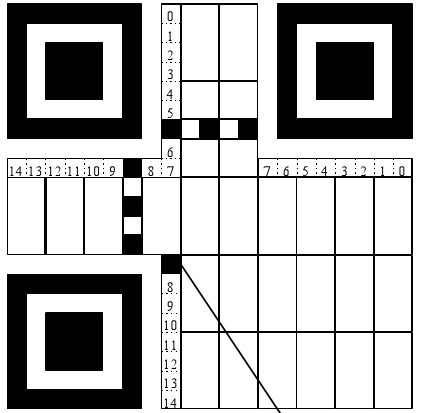
版本信息

Version Information 在>= Version 7的版本中，预留两块3*6的区域存放一些版本信息。

数据码字和纠错码字

除了上述的那些地方，剩下的地方存放 Data Code 数据码字 和 Error Correction Code 纠错码字。我们后面就简称数据码和纠错码，就是最前面两张图的深灰色区域，一般数据都是从右下角开始填充，先填充数据码，数据码填充完毕之后再填充纠错码，以version1为例，数据的填充顺序，是这样的：

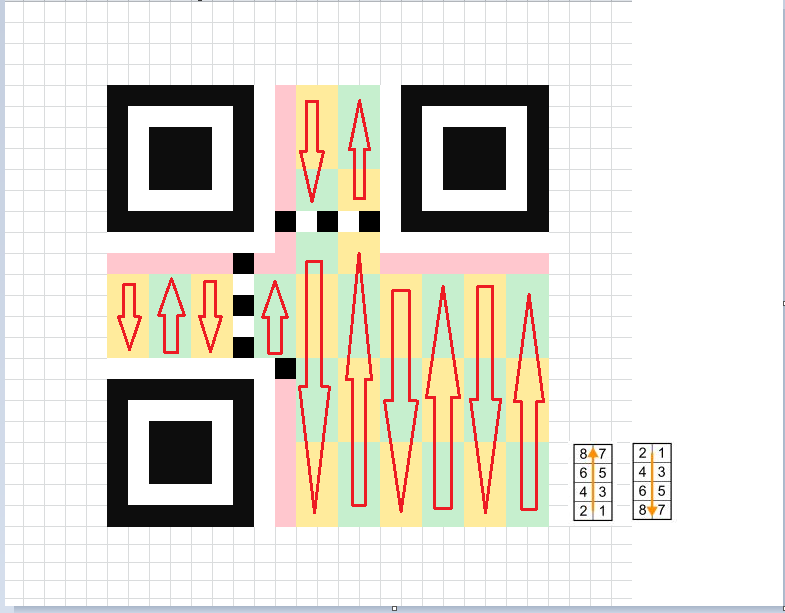
当然，随着版本的升高，会有越来越多的校正图形掺杂在其中，这样的话，数据填充可能就不是这么规矩的矩形了，但是总体的填充顺序不会大变化，都是先右后左的顺序。具体的可参考官方的文档。

数据编码与编码流程

QR码支持的数据编码

• Numeric mode（数字编码），从0到9。
• Alphanumeric mode（字符编码），包括0-9，大写的A到Z（没有小写），以及符号“$ % * + – . / : 空格”。
• Byte mode （字节编码），可以是0-255的ISO-8859-1字符。
• Kanji mode （日文编码），也是双字节编码。
• Extended Channel Interpretation (ECI) mode 主要用于特殊的字符集。并不是所有的扫描器都支持这种编码。
• Structured Append mode 用于混合编码，也就是说，这个二维码中包含了多种编码格式。
• FNC1 mode 这种编码方式主要是给一些特殊的工业或行业用的。比如GS1条形码之类的。

下表是每个模式的编码相对应的“编号”。

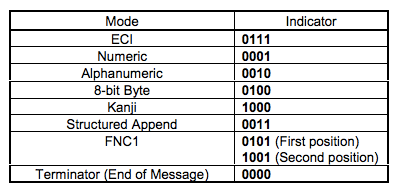
因为种类较多较复杂，而且为了方便大家理解，我们在这里值选择数字编码和字符编码举例，其它的编码，有兴趣的朋友可以查看官方文档。

示例一：

Numeric mode 数字编码，仅支持对从0到9的数字进行编码，也就是使用这个编码的二维码，扫描出来的内容只会是一串数字。如果需要编码的数字的个数不是3的倍数，那么，最后剩下的1或2位数会被转成4或7bits，则其它的每3位数字会被编成长度为10位的二进制数，最后将这些二进制数据连接起来并在前面加上编码模式的编号和字符计数指示符（就是表示了被编码的信息有多少个字符），字符计数指示符的长度取决于编码的模式和所要编成二维码的版本，在数字编码中，字符计数指示符如下表对应的有10、12或14位：

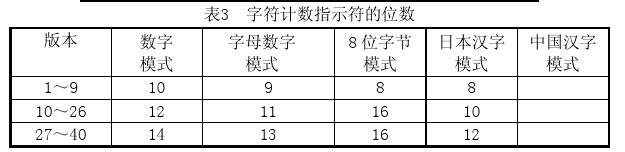
比如在Version 1的尺寸下，纠错级别为H（表示纠错等级为“高”，纠错级别我们会在下面讲到）的情况下，我们要编码的内容为：01234567

>   （1）. 按照每3个字符一组，把上述数字分成三组: 012 345 67
>   （2）. 把三位数的转成10bit二进制:012 转成 0000001100；345 转成 0101011001；两位数的67 转成7bit的二进制： 1000011。
>   （3）. 把这3个二进制串起来: 0000001100 0101011001 1000011
>   （4）. 把数字的个数（字符计数指示符）转成二进制 (version 1，纠错等级H，编码模式为数字编码，所以字符计数指示符的长度是10bit): 8个数字的二进制是 0000001000
>   （5）. 把数字编码的标志0001和第4步的字符计数指示符的编码加到前面: 0001 0000001000 0000001100 0101011001 1000011

示例二：

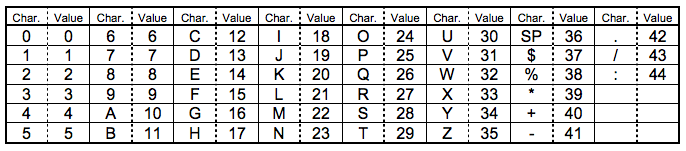
Alphanumeric mode 字符编码（也叫字母数字编码）。包括0-9，大写的A到Z（没有小写），以及符号“$ % * + – . / : 空格”。这些字符会映射成一个字符索引表。如下所示（两个表，中英文对照）：（其中的SP是空格，Char是字符，Value是其索引值）编码的过程是把字符转换为索引值，之后两两分组，按照特殊的算法转换成十进制的数值（这个算法，虽然简单，但是也是相当有想法，将前面的数值乘以45，加上后面的数值，组成一个十进制的数，这样在后期解码的时候，只用逆运算，用最后这个十进制的数除以45，得到的商和余数，就是原来的两个数），最后转成11bits的二进制，如果最后有一个落单的，那就转成6bits的二进制。而字符计数指示符需要根据不同的Version尺寸编成9,11或13个二进制（如上表）。

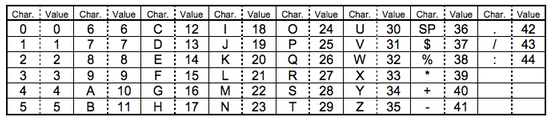
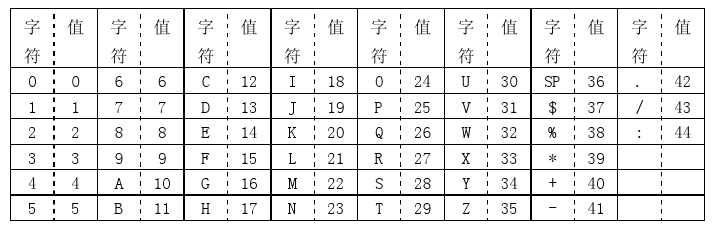
在Version 1的尺寸下，纠错级别为H的情况下，对“AC-42”进行编码：

>   （1）. 从字符索引表中找到 AC-42 这五个字条的索引 (10,12,41,4,2)
>   （2）. 两两分组: (10,12) (41,4) (2)
>   （3）. 把每一组转成11bits的二进制:第一组(10,12)，计算公式 10*45+12 = 462 转成 00111001110 ；第二组(41,4)，计算41*45+4 = 1849 转成 11100111001 ；第三组(2) 等于 2 转成 00001 。
>   （4）. 把这些二进制连接起来：00111001110 11100111001 000010
>   （5）. 把字符的个数（字符计数指示符）转成二进制 (Version 1-H为9 bits ): 5个字符，5转成二进制就是 000000101
>   （6）. 在头上加上编码标识 0010 和第5步的字符计数指示符编码: 0010 000000101 00111001110 11100111001 000010

结束符和补齐符

以上述示例一为基础，在编码结束后，我们得到了如下编码：

然后，我们还要加上结束符，表示真正的额数据已经结束。

按每组8个bit分组，如果所有的编码加起来不是8个倍数我们还要在后面加上足够的0，比如上面一共有45个bit，所以，我们还要加上3个0，然后按8个bits分好组：

00010000 00100000 00001100 01010110 01100001 10000000

再然后，就是补齐符（padding bytes），如果添加上结束符之后还没有达到我们最大的bits数的限制，我们还要加一些补齐码（Padding Bytes），Padding Bytes就是重复这两个bytes：11101100 00010001。（使用这两个字节的主要原因是，为了防止在填入数据时出现大片的深色或浅色区域，对扫描器产生干扰，使得二维码难以正常扫描），至于要补多少个补齐符，需要查看文档中相应的字符数和数据容量对应表，由于版本比较多，我们不一一列出，在官方文档中，我们示例相对应的是表7-表11。我们以下表为例：

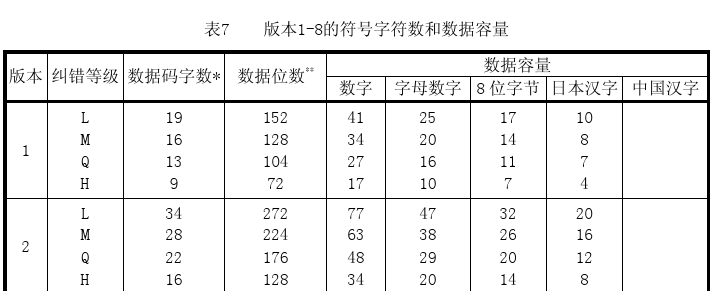
从表中，我们可以知道，version1-H的数据容量为9个数据码字（每个数据码字为8位），而我们上面已经有了6个数据码字，所以要补充三个8bit，补充完毕如下：

00010000 00100000 00001100 01010110 01100001 10000000 11101100 00010001 11101100

上面的每一组数据为一个数据码字，Data Codewords，现在也只是原始数据，还需要对其加上纠错码。

纠错码

上面我们提到了纠错级别，Error Correction Code Level，二维码中有四种级别的纠错（从低到高为L、M、Q、H），这就是为什么有人在二维码的中心位置加入图标，也依旧能够扫描的原因。（就是二维码残缺量不超过所对应的纠错等级允许的范围时，使用扫描工具依旧能扫描出内容的原因）。纠错等级对应的容错范围如下：

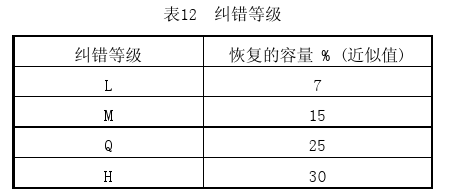
即只要二维码的损坏面积没有超过这个范围，理论上是可以恢复损坏的数据的。
至于纠错码是如何计算的，这涉及到里德-所罗门纠错算法（Reed-Solomon error correction），里德-所罗门码是定长码。这意味着一个固定长度输入的数据将被处理成一个固定长度的输出数据。在最常用的（255,223）里所码中，223个里德-所罗门输入符号（每个符号有8个位元）被编码成255个输出符号。大多数里所错误校正编码流程是成体系的。这意味着输出的码字中有一部分包含着输入数据的原始形式。符号大小为8位元的里所码迫使码长（编码长度）最长为255个符号。标准的（255,223）里所码可以在每个码字中校正最多16个里所符号的错误。由于每个符号事实上是8个位元，这意味着这个码可以校正最多16个短爆发性错误。
里德-所罗门码，如同卷积码一样，是一种透明码。这代表如果信道符号在队列的某些地方被反转，解码器一样可以工作。解码结果将是原始数据的补充。但是，里所码在缩短后会失去透明性。在缩短了的码中，“丢失”的比特需要被0或者1替代，这由数据是否需要补足而决定。（如果符号这时候反转，替代的0需要变成1）。于是乎，需要在里所解码前对数据进行强制性的侦测决定（“是”或者“补足”）。

这两段话是我抄的，什么意思我也不懂，但我们有现成的python模块来运算出纠错码——python的reedsolo模块，我们只要会用就行了，数学好的朋友可以去研究具体算法的实现。

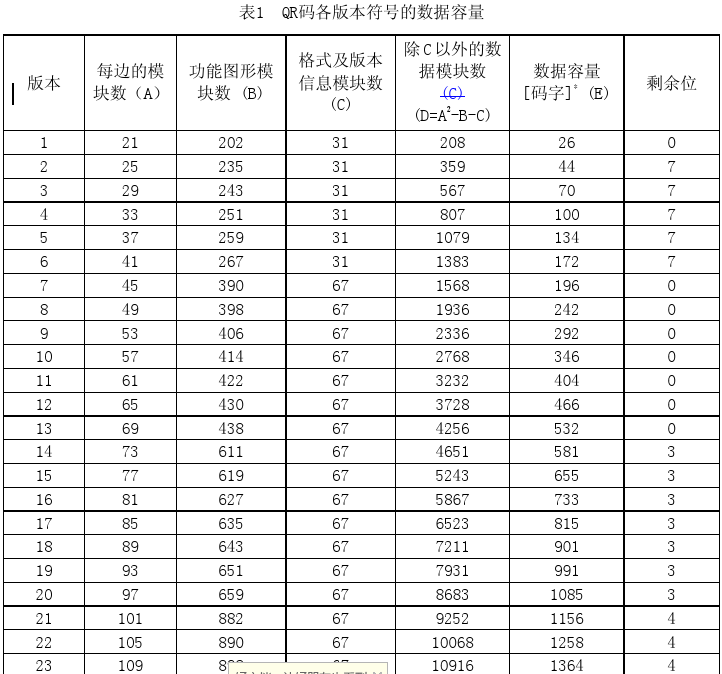
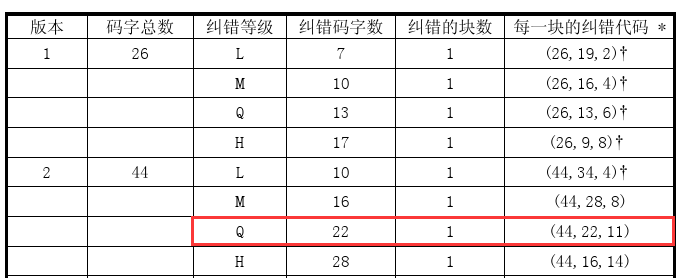
那么，哪个版本应该生成几个纠错码？我们可以对照官方文档中的纠错特性表，表13-表22。以下表为例：

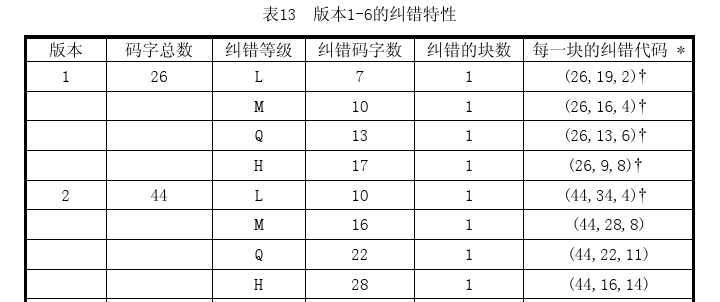
以版本1-H为例进行解释，从表中，我们可以清晰的知道，纠错码字数应该为17个，纠错的块数为1（表示这个版本要编码的数据只会分为一个数据块），（26,9,8）表示，这个版本的二维码总共可以存放26个码字，但是这26个码字中，有9个码字为数据码字，17个为纠错码字（8*2+1=17），8位纠错容量。每个表的下方附有注释信息：

这也是为什么纠错码字数为r2，当后面有一个箭头时，表示r2之后还要加1。
在给数据码字添加纠错码时，还有对数据码字分块的操作，因为version1的二维码对数据码字只分一个块，不够明显，所以我们采用网上的我所参考过的一个例子（现在不太容易找出处了，时间太久远了）：

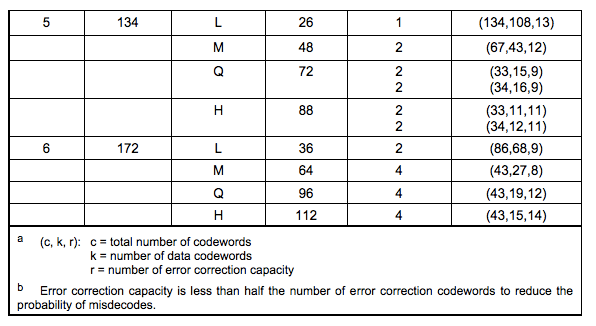
这个例子使用的是Version 5 Q纠错等级的二维码，从表中得知需要4个纠错块（2,2表示纠错块有两2组，每组2个），头一组的两个Blocks中各15个数据码字加上各18个纠错码字。
因为二进制写起来会让表格太大，所以，都用了十进制来表示，我们简述一下下表是如何生成的：在将数据编码之后，每8位分开，形成我们需要的数据码字，然后再将数据码字按照规定分成15:15:16:16的四组，分别进行纠错码的运算，生成的纠错码字数都是18。

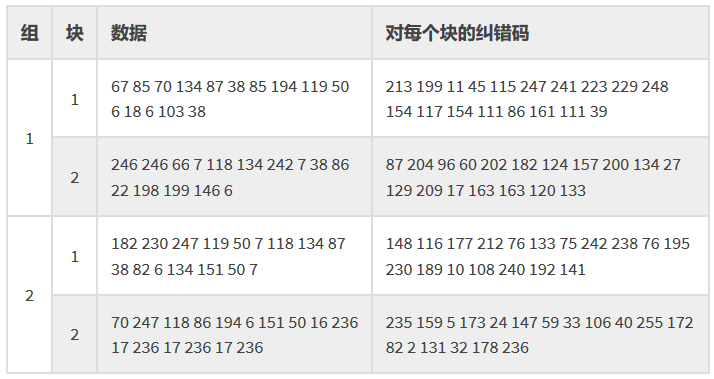
最终将这些码字穿插放置。但是也不是随意穿插，是数据码字与数据码字穿插，纠错码字与纠错码字穿插。
对于数据码字：把每个块的第一个数据码字先拿出来排列好，然后再取第一块的第二个，如此类推。上述示例中的数据码字Data Codewords如下：

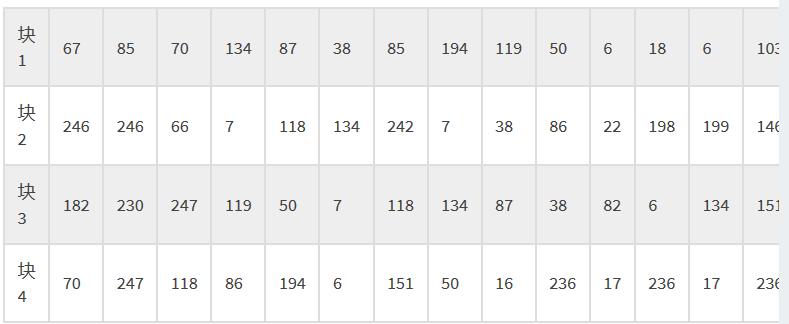
>   我们先取第一列的：67， 246， 182， 70
>   然后再取第二列的：67， 246， 182， 70， 85，246，230 ，247
>   如此类推：67， 246， 182， 70， 85，246，230 ，247 ……… ………，38，6，50，17，7，236

对于纠错码，也是一样：

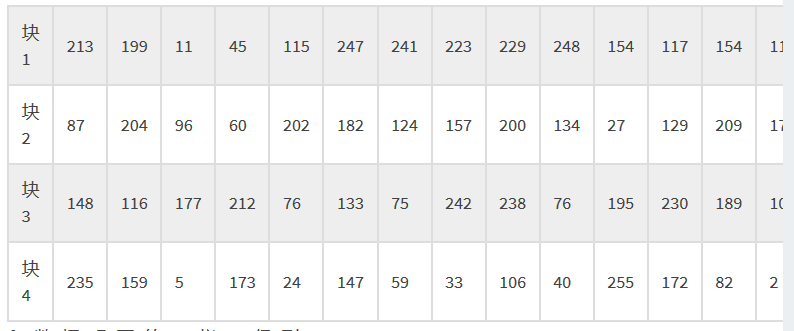
和数据码取的一样，得到：213，87，148，235，199，204，116，159，…… …… 39，133，141，236

然后，再把这两组放在一起（纠错码放在数据码之后）得到：

67, 246, 182, 70, 85, 246, 230, 247, 70, 66, 247, 118, 134, 7, 119, 86, 87, 118, 50, 194, 38, 134, 7, 6, 85, 242, 118, 151, 194, 7, 134, 50, 119, 38, 87, 16, 50, 86, 38, 236, 6, 22, 82, 17, 18, 198, 6, 236, 6, 199, 134, 17, 103, 146, 151, 236, 38, 6, 50, 17, 7, 236, 213, 87, 148, 235, 199, 204, 116, 159, 11, 96, 177, 5, 45, 60, 212, 173, 115, 202, 76, 24, 247, 182, 133, 147, 241, 124, 75, 59, 223, 157, 242, 33, 229, 200, 238, 106, 248, 134, 76, 40, 154, 27, 195, 255, 117, 129, 230, 172, 154, 209, 189, 82, 111, 17, 10, 2, 86, 163, 108, 131, 161, 163, 240, 32, 111, 120, 192, 178, 39, 133, 141, 236

Remainder Bits（剩余位）

最后再加上Reminder Bits，对于某些Version的QR，上面的还不够长度，还要加上Remainder Bits，比如：上述的5Q版的二维码，还要加上7个bits，Remainder Bits加零就好了。关于哪些Version需要多少个Remainder bit，可以参看官方文档的表一（这里列出一部分）。

掩码（也叫掩模）

编码的步骤是完成了，但是要想生成一个完整的二维码，还需要先将现在所拥有的数据填入提前准备的空白模板后，选择一个合适的掩码，将原模板的数据与掩码进行异或运算，最后，再将format information填进去就生成了二维码。

掩码存在的意义：二维码是要拿来扫描的，而扫描怕的就是无法清晰地分辨出编码信息的每一位。要是二维码中黑白点数量不均，或是空间分布不均都会导致大色块区域的出现，而大色块区域的出现会增加扫描时定位的难度，从而降低扫描的效率。更严重的情况下，如果数据填入后碰巧出现了功能性标识，比如定位标识的图样，还会干扰正常功能性标识的作用，导致QR码无法扫描。
在计算机科学中，掩码就是一个二进制串，通过和数据进行异或运算来变换数据。在QR码中，掩码也是通过异或运算来变换数据矩阵。QR码的掩码就是预先定义好的矩阵。QR标准通过生成规则定义了八个数据掩码(最后一个的编号，应该是111而不是110，图片错了)：

前面的三位二进制的数据就是每个模式掩码相对应的编号，这个信息也是要填入format information中的。具体的掩码图片是这样的：

从这个图我们就可以直观的看到每种掩码的模板样子，以掩码2（编号为010）为例，公式 j mod 3 = 0 就是表示从左边开始数，能被3整除的列，都要取逆（黑块变白块，白块变黑块），当然二维码的固定格式区域的信息是不用取逆的，所以要使用掩码2，需要取逆的列数为：0、3、6、9…..。

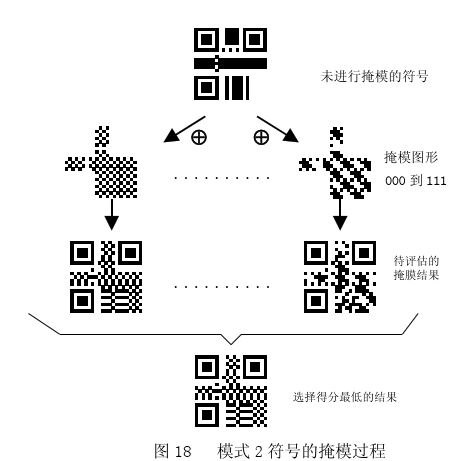
当然，官方规定在进行异或时，原始的数据模板要与每个掩码模板进行异或运算后，要进行如下的规则进行计分（处罚），最后选择分数最低的一个作为最佳的掩码选择。这里我们只做了解，不深入。

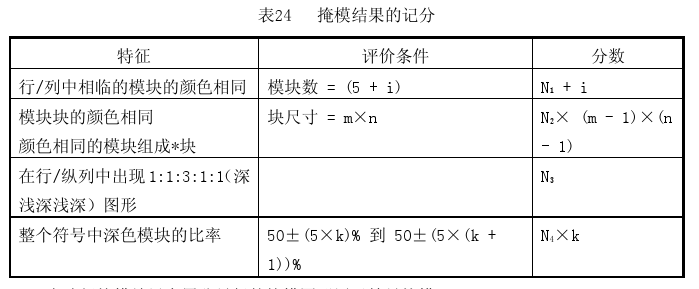
手绘二维码

在这一小节，我计划用excel手动画出一个二维码，目标是使用手机能够扫描出“HELLO”。

准备固定格式的填充模板

利用前面所学到的内容，就已经足够我们手动来描绘出一个简单的二维码，我们要画的是一个version1且容错等级为H的二维码，从上面的基础知识中知道，版本1的二维码尺寸为2121，所以我们整理出一个2121的表格（最好将每一单位的模块都调整成正方形），并提前画好version1二维码中的固定格式部分。如下图，是一个version1版本的二维码的所有固定格式。

进行数据编码

接下来就是对数据进行编码，由于进行编码的内容“HELLO”，全部为大写字母，且不存在特殊符号。所以这里选用字符编码是最方便的。

根据前面的示例，可以很简单的知道如何来运算得到二进制的数据：

1. 从字符索引表中找到“HELLO”相对应的值。（17,14,21,21,24）
2. 两两分组（17,14），（21,21），24
3. 把每一组转换成11bit的二进制：（17,14）：17*45+14=779=0b01100001011 ；（21,21）：21\*45+21=966=0b01111000110 ；24：0b011000
4. 把这些二进制连接起来：01100001011 01111000110 011000
5. 把字符的个数转成二进制，5个字符（“HELLO”），000000101
6. 再加上字符编码的标识0010，加起来就是0010 000000101 01100001011 01111000110 011000
7. 再加上结束符0000：0010 000000101 01100001011 01111000110 011000 0000
8. 按8bit重排，并补齐位数为8的倍数：00100000 00101011 00001011 01111000 11001100 00000000
9. 添加补齐码：00100000 00101011 00001011 01111000 11001100 00000000 11101100 00010001 11101100

计算纠错码

根据纠错特性表来进行分块和添加纠错码：

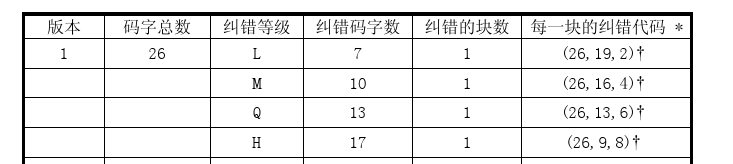
由表我们知道，码字总数为26，纠错码字数为17，再加上我们之前编码好的数据9个8bit，刚好是26.

计算纠错码：

码字整理

整理一下得到的码字：

>   数据码字：32，43，11，120，204，0，236，17，236
>   纠错码字：109，149，156，18，217，41，246，36，42，84，46，225，190，218，251，27，196

数据填充

得到所有的码字之后，就是简单但是麻烦的数据填充了：
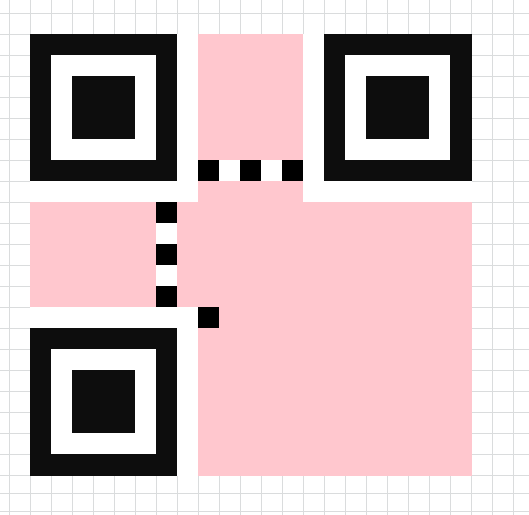
由于我们制作的是version1的二维码，所以不需要进行数据块的排序。直接按照如下的图片进行数据块的填充（先填充数据码字，再填充纠错码字）。

如：填充完第一个第二个数据码字的时候，应该是这个样子的：

全部填充完毕如下图，（剩下的粉红色的部分，是格式信息的位置，我们到后面再填充）：

将相应的format information信息填充进相应的区域。

• 纠错码等级：H 对应的编码为：10
• 掩码类别：2 对应的编码为：010
• BCH纠错比特：这里我们为了方便，直接查看对应关系，如下图，意思是一个二维码，如果它的纠错等级为H，所采用的的掩码为2，那么后面的二进制字符串即为它所对应的format information。参考地址：https://www.thonky.com/qr-code-tutorial/format-version-tables#list-of-all-format-information-strings
  
• 最终15个bit的数据为： 001110011100111

将其填充进format information数据区（注意填充顺序0-14所对应的是二进制的低位到高位）。

与掩码进行异或运算

我们前面提到，我们使用的是掩码2，也就是下面这个掩码：

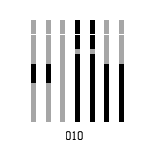
j mod 3 = 0 意思就是从左往右数，凡是能够被3整除的列，颜色都要取反（黑变白，白变黑）。我们将要进行反色的列标注出来（这里我是用的是在对应的列下方标粉色）。注意：功能性区域的不用取逆，就是一开始准备的固定格式的地方和之后的format information区域的数据，不用取逆。

手绘完成

OK，大功告成。现在用我们的手机就可以扫描了：

MMA2015-MISC400-qr二维码恢复挑战

学以致用，复现MMA2015-MISC400-qr的二维码恢复挑战的解题步骤，原版write-up地址为：
https://github.com/pwning/public-writeup/blob/master/mma2015/misc400-qr/writeup.md
我的恢复思路也是跟着wp来的。

注：python官方下载的reedsolo模块版本为0.3，不是很好用，所以我们这次使用write-up中推荐的版本，下载解压后运行python setup.py install即可。

题目分析

题目给出的二维码如下图：

根据对QR码的了解，知道这是一个25*25的二维码，也就是version2的二维码，从它能看见的部分我们可以得到format information的一部分信息：

??????011011010

获取格式信息

对照下面这个网址所给出的对应表，可以知道这个二维码使用了什么编码模式和使用了哪一个掩码

>   https://www.thonky.com/qr-code-tutorial/format-version-tables\#list-of-all-format-information-strings

经对照可知：

- 完整的format information信息应该是：010111011011010
- 且可以得到的信息还有该二维码使用的掩码为：6，对应的计算公式：( (ij) mod 2 + (ij) mod 3 ) mod 2 = 0
- 所对应的纠错等级为：Q

将被遮挡的固定信息部分以及format information信息补充完整。

获取原始码字

与相对应的掩码进行异或运算，得到原始的数据中的一部分数据码字和纠错码字。这个掩码对应的公式比较麻烦，且不容易计算，好在官方的文档中有提供各个掩码相对应的图案，如下图就是掩码6相对应的图案，如果不会计算公式，可以手动画一个与题目大小一样的掩码图，其对应的小图案大小是不变的，不同版本的二维码，只是小图案的数量不同：

将掩码应用到我们补充完的二维码上，翻转与掩码中深色区域相对应的区域的颜色，并用灰色将format information覆盖，方便读取数据，最后得到的如下图：

从右下角开始，按下图的蛇形顺序读取数据码字和纠错码字的信息，至于不同区域块的信息读取顺序，可以参考官方文档。

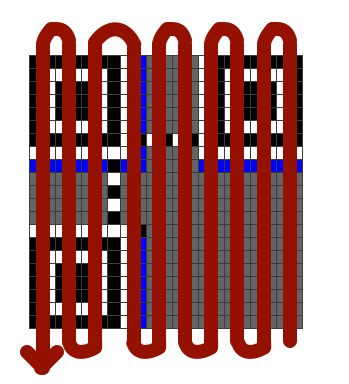
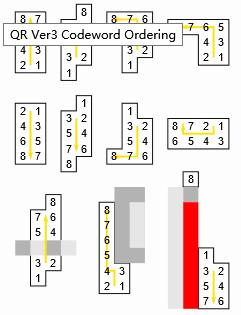
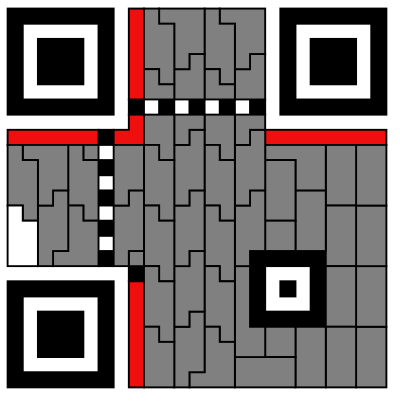
且相对应的数据块分布应该如下图所示：

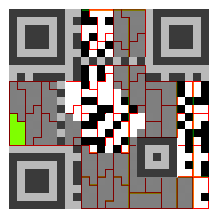
将全部可读的信息读取出来：

00100000 10100010 10111000 00111010 01011001 10011010 10001000 ????????
???????? ???????? ???????? ???????? ???????? ???????? ???????? ??00000?
1??????? ???????? ???????? ???????? ???????? ??010001 00100100 1???????
???????? ???????? ?????010 11000011 10000000 10101100 00010000 11100100
10101010 10011001 01100110 ???????? ???????? ?????0?0 0000000? ????????
???????? ???????? ???????? ????????

尽可能多地恢复数据

根据官方文档的纠错特性表，可知version2-Q的纠错码字数有22个，数据码字数也有22个，在Q级别，它可以恢复不超过25%的损坏的字节，但是我们只有16个完整的字节，即超过63%的字节丢失，但是Reed-Solomon的纠错能力很强，如果它知道错误在哪里，那么纠错能力就强得多，可以纠正多达两倍的擦除。但是这个比例也才只到50%，还不能直接把丢失的数据恢复出来。所以我们要想办法恢复一部分字节使得达到所拥有的完整数据有22个字节这个最低要求。

我们先将获得的可读取数据整理一下：

0010：【编码模式=字符编码（字母数字模式）】
000010100：【9个bit长度的字符计数标识符=20个字符】
01010111000：【FL】
00111010010：【AG】
11001100110：【 I】
1010001000？：【S?】

我们计算一下，22个数据码字，就是176个bit，而字符计数标识符表示总共有20个字符被编码，在编码的时候分为10组，每组11个bit，所以4+9+10*11=123个bit，也就是真正储存信息的数据码字共有123个bit，123/8=15余3，也就是结束符在第16个字节码，所以在第16个字节码的第4位开始，加上4个0（结束符），又因为8bit重组时需要补充为8的倍数，8-3-4=1，所以还需要加1个0。这时候总共也就16个数据码字，22-16=6，所以还要加上6个字节的补齐码，最终获得的数据码字的内容如下：

00100000 10100010 10111000 00111010 01011001 10011010 10001000 ????????
???????? ???????? ???????? ???????? ???????? ???????? ???????? ??000000
11101100 00010001 11101100 00010001 11101100 00010001

这样，我们就手动恢复了6个字节的数据，此时我们丢失的码字就只剩下22个了，正好达到了最低的要求。我们就可以使用纠错码恢复原本的数据。

编写脚本恢复

编写脚本利用python的reedsolo模块进行纠错（脚本文件已经存在与step3文件夹下）。

import sys
import reedsolo

reedsolo.init_tables(0x11d)

qr_bytes = '''00100000
10100010
10111000
00111010
01011001
10011010
10001000
????????
????????
????????
????????
????????
????????
????????
????????
??000000
11101100
00010001
11101100
00010001
11101100
00010001
00100100
1???????
????????
????????
?????010
11000011
10000000
10101100
00010000
11100100
10101010
10011001
01100110
????????
????????
?????0?0
00000000
????????
????????
????????
????????
????????'''.split()

b = bytearray()
erasures = []
for i, bits in enumerate(qr_bytes):
    if '?' in bits:
        erasures.append(i)
        b.append(0)
    else:
        b.append(int(bits, 2))
print erasures
print type(b)
for i in b :
	print '%x' % i

mes, ecc = reedsolo.rs_correct_msg(b, 22,erase_pos=erasures)
for c in mes:
	print '{:08b}'.format(c)

得到全部的信息：

00100000 10100010 10111000 00111010 01011001 10011010 10001000 00101111
10000110 11100010 10110110 10011001 01001010 11000011 00010101 00000000
11101100 00010001 11101100 00010001 11101100 00010001

拆分和解码

>   0010 [编码模式=字符编码]
>   000010100 [字符长度=20]
>   01010111000 ["FL"]
>   00111010010 ["AG"]
>   11001100110 [" I"]
>   10100010000 ["S "]
>   01011111000 ["G+"]
>   01101110001 ["JQ"]
>   01011011010 ["GA"]
>   01100101001 ["H:"]
>   01011000011 ["FW"]
>   00010101000 ["3X"]
>   0000 [结束符]
>   0 [8bit重组时补充的bit]
>   11101100 00010001 [补齐码]
>   11101100 00010001
>   11101100 00010001

二维码恢复挑战-二维码恢复工具

二维码恢复工具：qrazybox
工具下载地址：https://github.com/Merricx/qrazybox/tree/master/js

声明：
本次使用的题目是某次CTF比赛的题目，但是具体是哪次比赛的，我也不是很清楚。只是某天在群里划水的时候，间接得到了题目的文件，所以尝试进行了解答；由于是之后进行的回忆，自己也懒得再做一遍了，所以只能依靠当时解题时的一些零碎数据来拼凑一下完整的过程（我当时是手工做的，很费时间）。

> QRazyBox 是一个基于 Web 的应用程序（工具包），用于分析和恢复损坏的二维码。
> QRazyBox 允许您通过使用类似 Paint 的编辑器重新绘制和重建二维码来恢复二维码。
> 它还提供了几个子工具来帮助您更快、更高效地分析和恢复。

总体来说，这是一个辅助类型的工具，可以帮助你更好的分析损坏的QR码。

题目分析

这个题目的文件如下：

可以看到损坏的程度并不高（至少比上一道题少），我们先尝试手工读取内容，根据前面的知识，我们可以得知：

那么可以尝试将它画在excel表格中，并将缺失的定位点和格式信息补上：

整理已知信息

手动解码的步骤我们就不在这里描述了，我们直接放出解码时需要的内容：

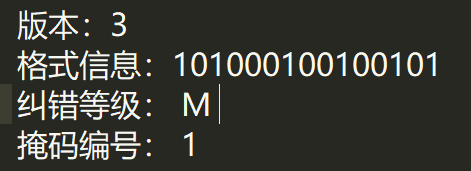
>   版本：3
>   格式信息：101000100100101
>   纠错等级： M 
>   掩码编号： 1 

恢复初始数据

计算掩码的行数与列数（python）：

for row in range(29):
	for column in range(29):
		if(( ((row * column) % 2) + ((row * column) % 3) ) % 2 == 0):
			print(str(row)+'--'+str(column)

手动将掩码反色的点返回来：

读取数据码字

01000001 11000111 10100110 10100110 00110111
01000110 01100111 10110111 10010011 00000111
01010101 11110110 01100011 00010110 11100110
01000101 11110110 11010110 01010101 11110011
00010110 11100101 11110111 00010111 00100110
00110011 00000110 01000011 00110111 11010000
???????? ???????? ???0?1?1 ?0?1?0?1 ?1?0?1?0
?0?1?0?1 11101100 00010001 11101100 00010???
???????? ???????? ???????? ???????? ????????
???????? ???????? ??????0? 0?1?1?1? 0?1?0?1?
0?101000 01110011 10011000 10100010 10011011
11010110 ???????? ???????? ???????? ????????
?1?01101 11001101 01101011 ???????? ????????
???????? ???????? ???????? ?0?10100 ????????
???????? ???????

整理信息

>   0100 = 编码模式 8-bit Byte
>   00011100 = 计数器 28

跟前面读取的数据比对一下，可以知道前28个码字都是完整的，这就意味着我们都不需要使用纠错码来纠错，直接读取就行了。

脚本读取

最后的解密代码：

s = '''01111010 01101010 01100011 0111
01000110 01100111 10110111 10010011 00000111
01010101 11110110 01100011 00010110 11100110
01000101 11110110 11010110 01010101 11110011
00010110 11100101 11110111 00010111 00100110
00110011 00000110 01000011 00110111 1101'''


ss = s.replace(" ","").replace("\n","")
flag = ''
for i in range(0,28):
	flag += chr(int(ss[i*8:(i+1)*8],2))
print(flag)

将上面的代码运行，即可得到最终的flag。

使用工具恢复

现在我们讲如何使用工具：
从github上将qrzybox-master下载下来，将index.html文件拖入浏览器中打开，然后点击“new project”--> “import from image”，然后将“恢复固定格式.png”导入：

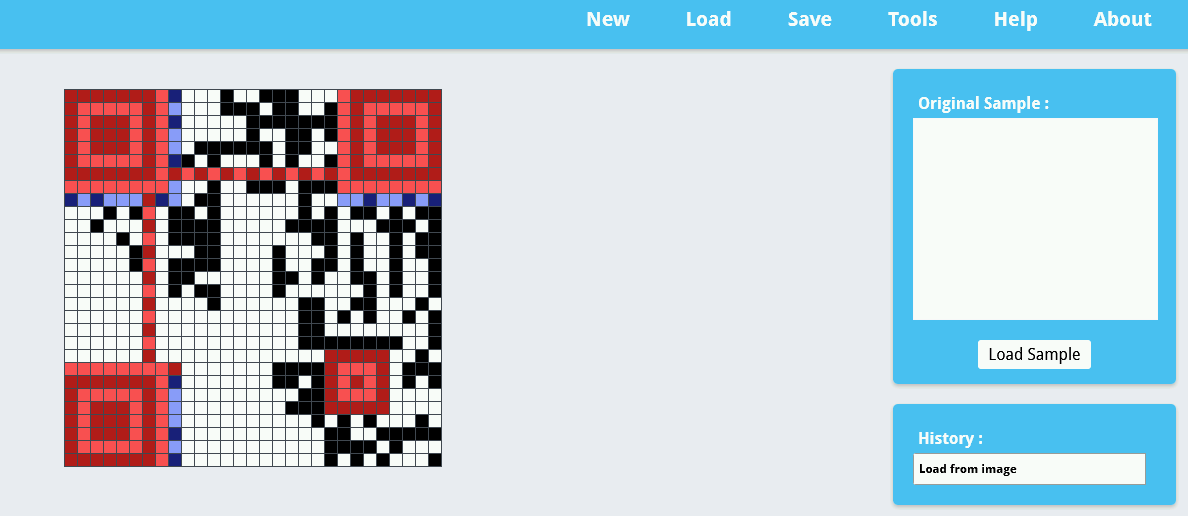
然后点击“tools”-->“Extract QR information”,即可恢复数据:

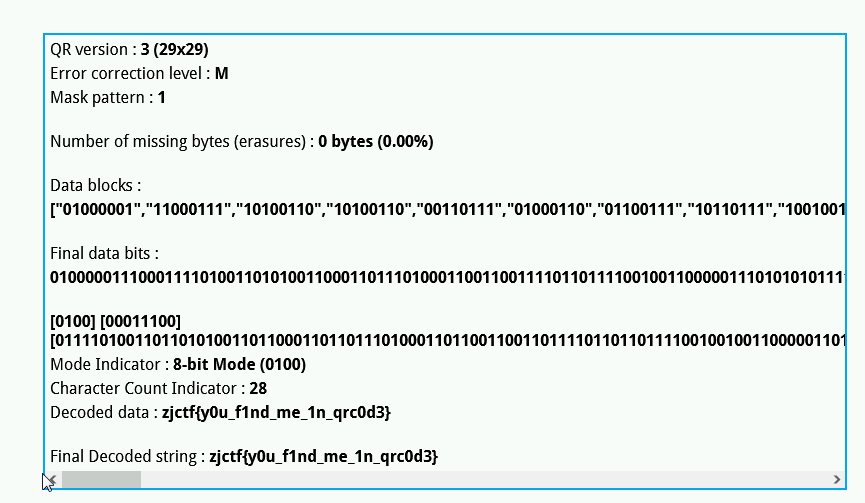
就这么简单，当然这个工具还有很多其他的用处，就开大家自己去研究了。

参考文章

二维码生成细节和原理：

https://zhuanlan.zhihu.com/p/21463650

https://coolshell.cn/articles/10590.html

官方文档（中文版）：

https://wenku.baidu.com/view/ef77275f312b3169a451a4a4.html?pn=50

里德-所罗门码：

https://www.jianshu.com/p/8208aad537bb

https://en.wikiversity.org/wiki/Reed–Solomon_codes_for_coders#Encoding_outline

https://stackoverflow.com/questions/30363903/optimizing-a-reed-solomon-encoder-polynomial-division

MMA2015-MISC400-qr的write up

https://github.com/pwning/public-writeup/blob/master/mma2015/misc400-qr/writeup.md