摄像机标定
1 摄像机标定
在摄像机几何模型中，我们得到了摄像机模型变换矩阵为
，其中，K为摄像机内参，R,C为摄像机外参。
为了方便后续推导方便，对公式符合做出一些修改：
1）使用T代替-C表示平移参数，
；
2）摄像机内参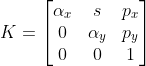
在引入像平面扭曲变换（skew）时引入了s后导致参数
不再只表达y轴上的缩放信息，
因此在后续参数分解中存在麻烦，更好的表达方式为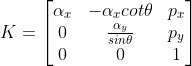
，
描述了像平面上xy轴间的夹角；
现在不考虑摄像机内外参细节内容，投影变换矩阵P是一个3*4的变换矩阵，其自由度为11， 只需保证12个元素间的比值一致即可表示同一变换，
因此，该变换实际上少了一个缩放尺度，在三维信息恢复中只能得到一个任意缩放尺度的恢复。
对于摄像机模型参数标定，只需要建立起三维坐标点与图像点之间的足够多映射（11个映射关系），即可求解变换矩阵。
选择映射点需要注意以下两点：
1）选择远多余6对点建立映射关系以确保鲁棒性；
2）三维空间点不应该来自同一个平面，这样会得到一个退化的方程组；
将变换矩阵表达为
，有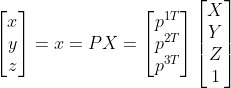
，
，
，这里向量与标量没有特别标注，需根据语境理解。
以上表达式中，x与X分别表示图像空间与三维空间中点的坐标，为已知值，P为待求未知量。
一个映射可建立两个方程，待人多个映射整理得：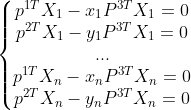
，令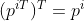
，待求矩阵P可改写为列向量
，
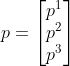其他已知量被整理到已知矩阵
，因此得到超定方程组Mp=0。
对于一个齐次线性方程组，需要注意两点：
1）p=0满足方程组，但显然不是我们需要得解；
2）假设
满足方程组，则任意实数点乘
同样满足方程组 ；
基于以上原因，Mp=0求解需要转化为一个约束问题，即满足p的模长为1情况下求变换Mp的模最小时对应的p。
也就是说对单位向量p施加一个线性变换M，使得变换后的向量模长最短！
对M进行SVD分解得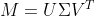
，
，
由于V为向量正交，当p取V中对应的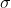
值最小向量，可以使得
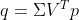一个模长趋近0的向量，
由于U也为正交向量，||Uq||=||q||，所以经过Uq变换后得到的模长也是趋近0，因此找到了一个最优解！
2 提取摄像机参数
当完成标定后，我们得到了一个投影变换矩阵P，该矩阵描述了相机变换的内外参数，在应用中需要根据变换矩阵P求解具体内外参数。
首先列举处内外参数表达式如下：
，
，
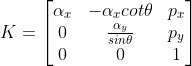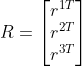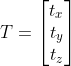，将矩阵P写成
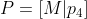，其中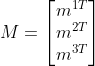
，
首先求摄像机内参数，建立等价关系
，
观察上式可知
，由于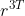
为旋转矩阵的一个行向量，其模长为1，可得
；
由于
，由于旋转矩阵的各个行向量正交，可得
；
同理得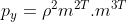
；
接下来求解相机扭曲角度，由于合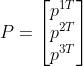
矩阵的行向量分别代表相机中心与图像y坐标构成平面，相机中心与图像x坐标构成平面和主平面，
则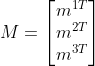的行向量表示对应平面上的法向量，
得到图像平面x轴方向向量， 
得到图像平面y轴方向向量，
使用余弦公式可得
；
根据等价关系得
，取模得
，
整理得
，由于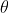
已经求出，则可以求得
；
同理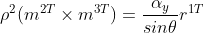得
，取模得
，则可求得
；
以上有两点注意：1）由于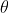取值在0到180度，所以无需关注符号，2）,的符号目前未知。
接下来求摄像机外参数，已知等价关系和，可以求出旋转矩阵行向量
；
通过等价关系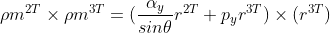
可得
，已知旋转矩阵行向量为单位向量，故该计算是可行的；
利用旋转矩阵正交关系，可得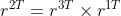
，到此计算出了所有的旋转向量；
对于平移信息，有等价关系
，这里仅有T是未知量，K为一个上三角矩阵，直接回代即可求解T。
参考资料：计算机视觉之三维重建 鲁鹏
