通用函数求导
1 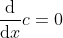 ,c 为常数;
,c 为常数;
2  ,n 为任意有理数,证明如下:
,n 为任意有理数,证明如下:
1)当 n 为正整数时,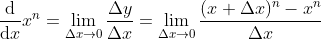 ,
,
使用二项定理  ,
,
 ;
;
2)当 n 为负整数时,令 m = -n, 则 m 为正整数,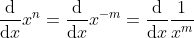 ,
,
使用求导除法规则 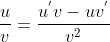 ,
,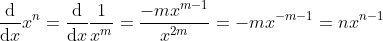 ;
;
3)当 n 为零时,自然满足公式;
4)当 n 为有理数时,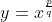 ,等式可改写为
,等式可改写为 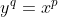 ,利用隐函数求导有:
,利用隐函数求导有: ,
,
整理得: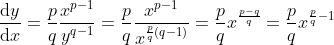 ;
;
3 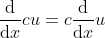 ,c 为常数;
,c 为常数;
4  ,u,v 为不同函数;
,u,v 为不同函数;
5 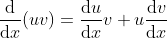 ,证明如下:
,证明如下:
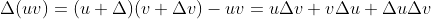 ,
,
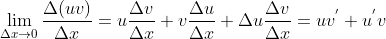 ;
;
6 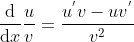 ,证明如下:
,证明如下:
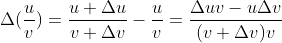 ,
,  ;
;
7 复合函数 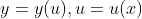 ,
,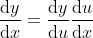 ,证明如下:
,证明如下:
 ,对其求极限得:
,对其求极限得: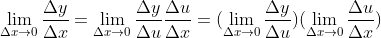 ,
,
由于 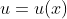 为连续函数,根据连续性得:当
为连续函数,根据连续性得:当  时,
时,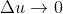 ,
,
可得 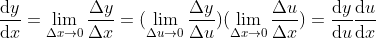 ;
;
8 三角函数求导
1)在半径为 1 的单位圆周上任意点 (x,y) 对应的基本三角函数有:
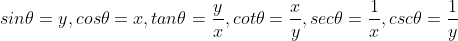 ,
,
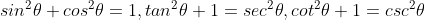 ;
;
2)当 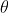 以弧度计量时,
以弧度计量时,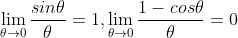 ,证明如下:
,证明如下:
a. 在单位圆中, 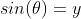 ,
, 为该角度对应的弧长,当
为该角度对应的弧长,当  趋近无穷小时,两者相等,等式
趋近无穷小时,两者相等,等式  成立;
成立;
b.  ,
, ;
;
3)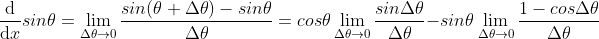 ,
,
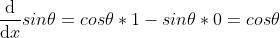 ;
;
4)使用相似方法可证明 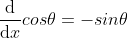 ;
;
5)利用复合求导规则,可以推导出其他基本三角函数导数,如下:
 ;
;
9 反三角函数求导
1)对反三角函数 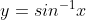 求导等价于对
求导等价于对 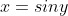 求导,
求导,
应用隐函数求导规则有  ,
,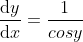 ,
,
由  得
得 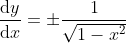 ,
,
由于 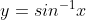 在定义域内为单调递增函数,故
在定义域内为单调递增函数,故 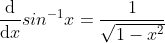 ;
;
2)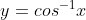 等价于
等价于  ,
, ,
,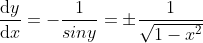 ,
,
由于 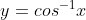 在定义域内单调递减,故
在定义域内单调递减,故 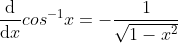 ;
;
3)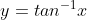 等价于
等价于 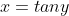 ,
,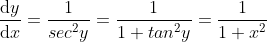 ;
;
4)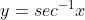 ,
, ,
,
由于 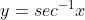 在定义域内单调递增,
在定义域内单调递增,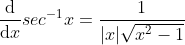 ;
;
5)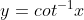 ,
, 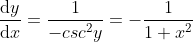 ;
;
6) ,
,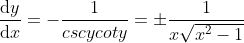 ,
,
由于  在定义域内单调递减,
在定义域内单调递减,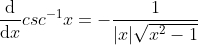 ;
;
10 指数与对数函数求导
1)指数基本运算法则是显然的,包括:
 ;
;
2)对数基本运算法则需要一些推导,包括:
. 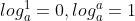 ,由于指数与对数互为反函数关系,该结论是显然的;
,由于指数与对数互为反函数关系,该结论是显然的;
.  ,通过关系式
,通过关系式  可推导结论;
可推导结论;
.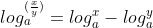 ,通过关系式
,通过关系式  可推导结论;
可推导结论;
.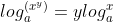 ,通过关系式
,通过关系式 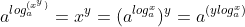 可推导结论;
可推导结论;
.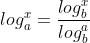 ,欲证明该等式成立,可转换为证明
,欲证明该等式成立,可转换为证明 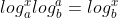 是否成立,
是否成立,
两边取对数 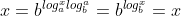 可证明等式成立;
可证明等式成立;
3)极限 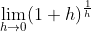 存在?
存在?
通过对对数函数求导运算,可证明极限  为一个有限实数,具体如下:
为一个有限实数,具体如下:
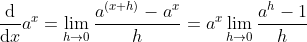 ,
,
当 x = 0 时有  ,观察图形在该点出导数为有限实数,则极限
,观察图形在该点出导数为有限实数,则极限 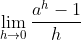 为有限实数,
为有限实数,
令  ,等式可变换为
,等式可变换为  ,
,
令  ,上式可改写为
,上式可改写为 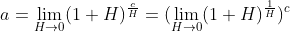 ,
,
最终得到 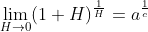 ,则极限
,则极限 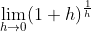 存在。
存在。
4)求导 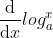 ?
?
 ,
,
令 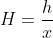 ,有
,有 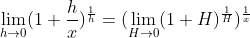 ,
,
现在设 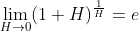 ,当对数底为
,当对数底为  时,对数求导结果最为简化,
时,对数求导结果最为简化,
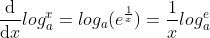 ,得到任意底对数函数导数;
,得到任意底对数函数导数;
当对数函数底为 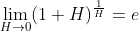 时,有
时,有  。
。
5)指数函数  求导
求导
将指数函数改写为对数函数 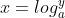 ,
,
利用隐函数求导规则有  ,
,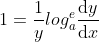 ,
,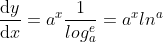 ;
;
当指数函数为 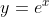 时,
时, 。
。
参考资料 Calculus With Analytic Geometry George F. Simmons
The Calculus Lifesaver Adrian Banner





