SIFT
SIFT(Scale Invariant Feature Transform) 由 David Lowe 于 2004 年提出。SIFT 算法在不同尺度下检测最强特征点，并给出特征点描述。由于特征点描述基于主方向与尺度信息，故可以使用描述信息对不同尺度，不同方向特征点进行比对。主要步骤如下：
1）使用不同尺度 DoG 算子在 （图像平面，尺度）空间上寻找极值；
2）使用 二次函数 极值确定特征点精确位置与尺度，剔除无小特征点；
3）使用 梯度 信息确定各个特征点方向；
4）基于 特征点方向与特征点尺度 计算特征点描述信息；
1 检测尺度空间上极值
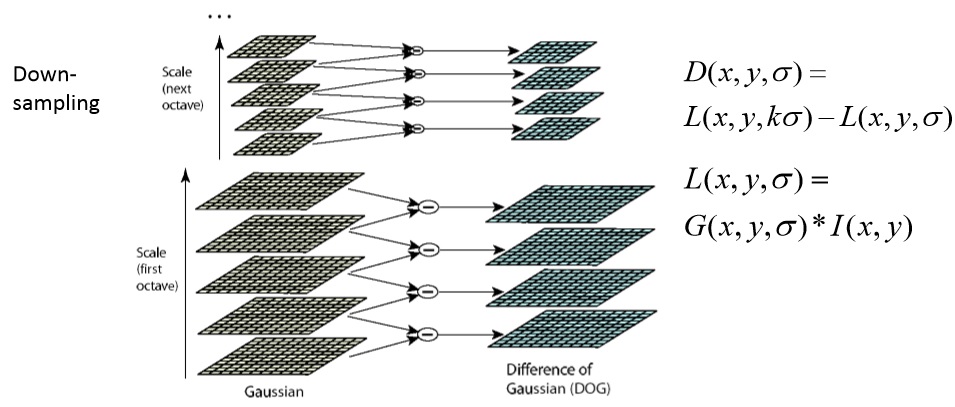
与 "Blob检测" 博文大体一致，使用不同尺度 高斯函数 对原图像卷积，再对卷积图像求差值，得到原图像不同尺度下的 DoG 响应。
将不同尺度下 DoG 排列起来即形成了一个三维函数，其因变量为：位置(x, y)， 尺度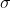 
，
。
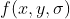在离散函数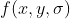 
上，对比每个点与周边 26 个邻接点关系，当其值均大于邻接点值或者均小于邻接点值时，确定为候选特征点。如下图：
在使用 Laplacian of Gaussian 检测关键点时，不同尺度高斯函数产生的响应不一致，需要使用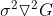 
进行归一化处理。
而 DoG 等价于 归一化 LoG， 推论如下：
1）根据 heat diffusion equation ，该微分方程描述了温度随时间的变化量与随位置变化量之间的关系；
2）通过类比，将不同尺度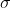 
当作热传导中的时间变量，将 (x,y) 当作热传导中的空间变量，得 
；
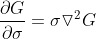3）使用 difference of gaussian 近似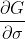 
，得 
，
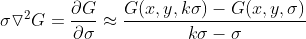进一步化简得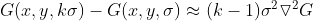 
。
2 提升特征点位置精度
将函数 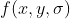视为连续函数，利用二阶泰勒公式可以得到特征点更精确位置与尺度，具体如下:
1）以离散情形下计算特征点位置作为起始点，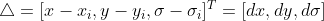
表示相对于起始点偏移量；
2）二阶泰勒表达式为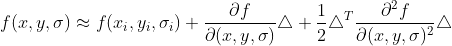 
；
3）对二阶泰勒表达式求一阶偏导并令其值为0
，
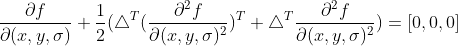由于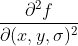 
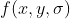为函数 在点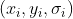 
的二阶导数构成的 Hessian 矩阵，根据对称性上式简化为
，
，
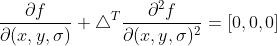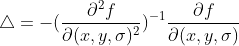得到极值点（即为精确位置）为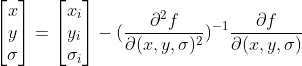 
。
3 剔除无效特征点
1）将函数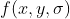 
取绝对值并归一化为 
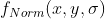， 排除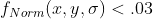 
对应的极值点。
2）使用 Hessian 矩阵剔除边缘响应，思路如下：
当使用 difference of gaussian 对图像卷积时，图像边缘会产生很强响应，而边缘点不是良好的特征点。
对边缘点求 Hessian 矩阵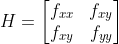 
，其特征值 
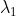远大于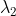 
，可以利用特征值的这种特性剔除边缘点响应。
对于 2 * 2 矩阵，可以使用矩阵的迹与行列式间接表示特征值，如下：
，
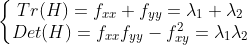令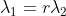 
， 
，
通过以上关系，假如需要排除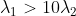 
的响应点，仅需验证 
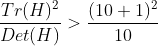是否成立即可。
4 确定特征点主方向
在特征点附近通过梯度直方图，可以统计出该特征点主方向。使用该主方向描述特征点，使特征点具有旋转不变性。
1）选择特征点对应尺度图像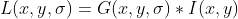 
；
2）求特征点附近窗口梯度幅度与方向
，
；
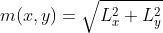3）构造 36 bins 梯度直方图，各点梯度强度使用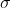 
为 1.5 倍尺度的高斯函数 加权；
4）使用梯度直方图峰值作为该特征点主方向，当存在双峰且第二峰值大于第一峰值的 80% 时，
该特征点被认为存在两个主方向，也可认为是两个特征点，只是位置与尺度相同而已。
5 特征点描述
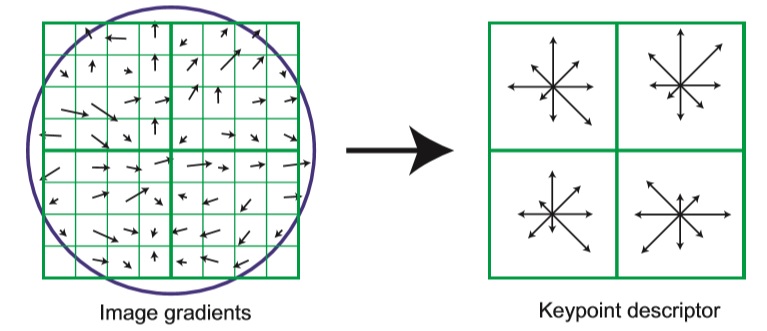
1）将特征点附近划分为 4*4 小区域（上图使用 2 * 2 划分），其区域大小与特征点尺度相关；
2）对每个小区域建立 8 bins 梯度直方图，梯度强度使用高斯函数加权；
3）使用主方向排列每个小区域内梯度方向；
4）对于光照变化引起的仿射变换，对每个小区域内梯度直方图归一化处理，消除光照变化影响；
5）如果光照变化引起非线性变换，如相机饱和，不同朝向3D表面引起，光照变化会对梯度幅度造成非线性变化，但一般不影响梯度方向。
因此， 在归一化梯度直方图上，当梯度强度大于.2 时直接设置为 .2，并再次对梯度直方图归一化处理，这样可得到一个对光照较为稳定的特征点描述。
综上，特征点描述由 4 * 4 * 8 维向量构成，每个分量取值范围为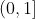 
。
6 opencv 实现
opencv 提供了 SIFT 实现，其构造函数如下：
SIFT( int nfeatures=0, int nOctaveLayers=3, double contrastThreshold=0.04, double edgeThreshold=10, double sigma=1.6);
nfeatures：表示最多检测特征点数量，当为默认值0时，返回所有特征点；
nOctaveLayers：检测尺度空间上极大值使用层数为 nOctaveLayers + 3；
contrastThreshold：归一化函数 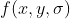，当极大值小于 contrastThreshold 时剔除；
edgeThreshold: 使用该参数剔除边缘特征点，与 contrastThreshold 相反，当 edgeThreshold 越小，剔除点越多；
sigma：使用该值对图像进行预处理（平滑处理）；
SIFT 可以分别检测特征点和描述特征点，也可以将其在一个函数中完成，这样可以提升处理效率；
当检测并描述特征点后，使用 DescriptorMatcher 对特征点进行匹配，DescriptorMatcher 有很多派生类实现不同匹配方法，匹配结果存放在 DMatch 中；
对于大量特征点匹配，其中存在不少匹配错误，可以采用一些方案进行筛查，如：
1）特征向量匹配的最近欧式距离与次近欧式距离应满足关系，最近欧式距离 < 次近欧式距离 * 0.7；
2）取特征向量匹配最小距离的两倍最为“正确”匹配阈值；
以下给出使用 SIFT 进行特征匹配的代码：
1 cv::Mat img1 = cv::imread("a.jpg", cv::IMREAD_GRAYSCALE); 2 cv::Mat img2 = cv::imread("b.jpg", cv::IMREAD_GRAYSCALE); 3 4 cv::SiftFeatureDetector detector(100); 5 std::vector<cv::KeyPoint> keypoints1, keypoints2; 6 cv::Mat descriptors1, descriptors2; 7 detector.operator()(img1, cv::noArray(), keypoints1, descriptors1); 8 detector.operator()(img2, cv::noArray(), keypoints2, descriptors2); 9 10 cv::BFMatcher matcher(cv::NORM_L2); 11 std::vector<DMatch> matches; 12 matcher.match(descriptors1, descriptors2, matches); 13 14 cv::Mat img_matches; 15 cv::drawMatches(img1, keypoints1, img2, keypoints2, matches, img_matches); 16 cv::imwrite("c.jpg", img_matches); 17 18 double max_dist = 0; 19 20 for (int i = 0; i < matches.size(); i++) 21 { 22 double dist = matches[i].distance; 23 if (dist < min_dist) min_dist = dist; 24 } 25 26 // Draw only "good" matches (i.e. whose distance is less than 2*min_dist, 27 // or a small arbitary value ( 0.02 ) 28 std::vector< DMatch > good_matches; 29 30 for (int i = 0; i < matches.size(); i++) 31 { 32 if (matches[i].distance <= max(2 * min_dist, 0.02)) 33 { 34 good_matches.push_back(matches[i]); 35 } 36 } 37 38 cv::drawMatches(img1, keypoints1, img2, keypoints2, good_matches, img_matches); 39 cv::imwrite("d.jpg", img_matches);
参考资料 Distinctive Image Features from Scale-Invariant Keypoints David G. Lowe
Learning OpenCV 3 Adrian Kaehler & Gary Bradski
