有向图与关联矩阵

    使用线性代数可以更好理解图相关知识。图由顶点与边组成，以下有向图可以使用关联矩阵表示：

       

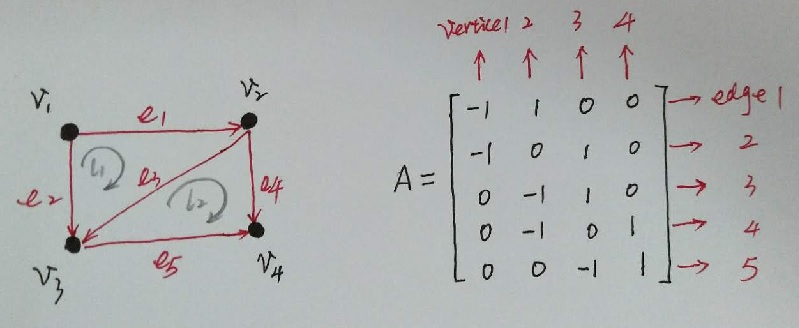
    矩阵 A 每行表示一条有向边，每列表示一个顶点信息。该图可以表示一个无源电路系统，通过考察矩阵 A 的四个基本子空间，可以有效理解该电路系统。

    矩阵 A 的零空间

    通过求解 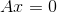，其解 x 位于矩阵的零空间。展开方程得如下关系：

      ，。

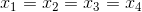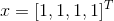    通过以上关系，可知 位于矩阵 A 的零空间中，同时以上方程组无法推导出更多的关系，故 是矩阵 A 零空间的唯一基，也即矩阵 A 的秩为 3。

    方程 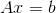 可展开为：

      ，表示个节点直接的电势差。

    由于 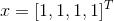位于零空间，其解为 。

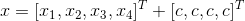    矩阵 A 的列空间

    通过以上分析，矩阵 A 的秩为 3，根据 Kirchhoff"s Voltage Law，回路1 与 回路2 上的电势差为0，可建立如下关系： 

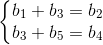       ，该关系表示矩阵 A 列空间，向量 b 包含 5 个变量，但有两个相关等式，满足矩阵 A 的列空间的维数为 3。

    以上关系表示有向图上符合条件的电势差必须满足等式 。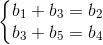

    矩阵 A 的左零空间

    通过求解 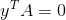，其解 y 位于矩阵的左零空间，表示各条边上的电流，

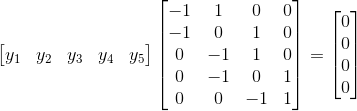     ，展开方程组得：

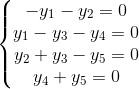    ，其中，每一个等式表示经过结点的电流为零，故矩阵的左零空间描述了 Kirchhoff"s Current Law。

    通过求解以上方程组，可以得到矩阵 A 的左零空间，但可以根据矩阵 A 的列空间推导出矩阵 A 的左零空间，具体如下：

    1）左零空间 垂直于 列空间；

    2）列空间的维数为 3，矩阵列数为 5，则左零空间的维数为 5 - 3 = 2；

    3）矩阵的列空间满足 ；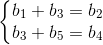

    4）关系 3）可改写为 ，由于 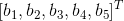位于列空间，

       则 与 位于矩阵的左零空间，并构成左零空间的一组基。

    矩阵 A 的行空间

    由于矩阵的行空间与矩阵的零空间正交，且已知矩阵 A 的零空间为 ，则矩阵 A 的行空间的维数为 3，并满足关系

    。

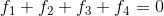    以上关系可以使用矩阵表达式简明表达：

    1）各节点电势差为 ；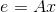

    2）根据电势差可求得电流 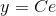，C 为常数；

    3）流入与流出各个节点电流和为零 ；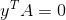

    4）整理可得 ；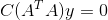

    5）当外接电流源时，可表示为 ；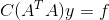

    通过各个子空间的维度关系，可以推导图的一个重要的公式：欧拉公式，具体如下：

    

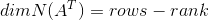
    #loops = #edges - (columns - 1)

    #loops = #edges - (#nodes - 1)

    #edges - #nodes + #loops = 1

 

    参考资料 Linear Algebra And Its Applications   Gilbert Strang