稠密光流

1 运动场与光流

    当物体与相机存在相对运动时，在视频序列中，物体所成的图像会发生相应的变化。这些变化可以恢复物体与相机间的相对运动，以及物体的形状。

    物体的每一点上的运动速度构成了运动场，物体在图像序列中所表现得明暗变化称为光流，一般情况下，可以使用光流描述物体运动。

 

 2 光流约束方程

     当图像序列以速度 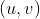 运动， 时间后运动距离为 ，光流约束方程可表示为：，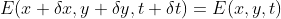

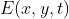      是关于 x,y,t 的连续函数，使用泰勒级数对  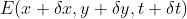做一阶近似为：，

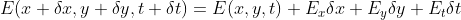     带入光流约束方程得：，

     两边同时除以 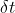 得：。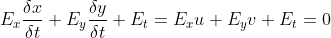

     对于图像上任意点的光流 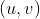，满足以上约束方程，其中， 为图像偏导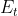， 为图像帧间导数。

     从以上方程中可知，需要更多信息来求解图像光流速度。在 LK 光流中，通过建立角点附近的超定方程组来求解光流，这避免了光流求解的孔径问题。在稠密光流中，需要增加附加信息来求解光流。

 

 3 光流光滑性约束

    在刚体运动中（或类似刚体），一般满足光流速度场是连续变化的。通过最小化 ， 使得光流满足连续变化。

    同时，光流约束方程可转化为最小化 。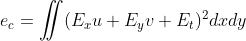

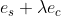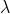    最终，将光流问题转换为最小化 ，其中， 为权重系数，当图像噪声过大使用较小 ，当图像噪声较小时使用较大 。

    最小化  可转化为变分问题，下面对离散情形进行讨论：

    对图像上任意点，，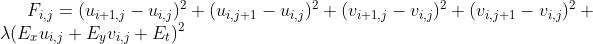

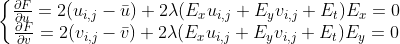    最小化  转换为 ，其中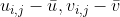， 为 u, v 的 Laplace 算子的离散形式，

    进一步改写为 ，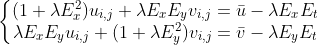

    求解得 ，

    改写为迭代方法为 ，

    初始光流为零，通过迭代可逐步求得各点光流速度。对于光滑平面，其光流速度等于其周边平均速度，通过足够的迭代就可以计算每一点的光流速度。

 

4 Dual TV-L1 Algorithm

   将函数  改进为 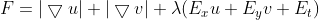 即为 Dual TV-L1 算法。

   opencv 提供了 OpticalFlowDual_TVL1 实现了 Dual TV-L1 Algorithm，其可调节参数包括：

   tau，theta：控制迭代收敛速度，tau 越大或者 theta 越小，迭代速度越快；

   lambda：表示最小化函数中平滑项所占的权重；

   nScales：控制金字塔层数；

   swaps：表示在每层金字塔上，光流速度迭代计算次数；

   epsilon，iterations：控制迭代精度；

   usingInitialFlow：使用初始化光流作为参考估计。

 

  5 Faerneback Polynomial Expansion Algorithm

     Faerneback 算法使用多项式拟合平面方式评估图像中各个点的运动情况，其拟合平面方程为：。

    当图像发生较小平移时，在视频序列中同一点拟合的二次多项式也同样存在一个平移关系：，由于 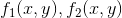 已知，则可以求解出 。

    在一维图像下，拟合前后两帧图像相同位置附近区间的二次曲线，通过模型 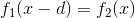 可求解偏移量 d。如下图：

      

    下面给出更加详细的解释：

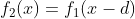     1）在图像序列中某一点上以一定窗口尺寸拟合二次曲线 ，设两帧间运动距离为 d，使用等式  可得：

          ，

          ，可求解 ，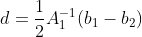

          当拟合趋近越小，更细小的变化可被拟合，当拟合区间越大，更大的变化可被拟合，故需要选择一个合适的拟合区间；

     2）由于在实际拟合中存在噪声干扰，等式 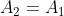 并不一定能够满足，可以通过一些近似方法减少噪声影响，

          令 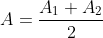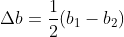，，有 ；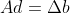

     3）如果对图像中每一点计算光流，其噪声很大。假定光流缓慢变化，可以使用区域来降低噪声，

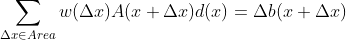          ，求解线性方程组即可得到更加稳定的光流；

     4）当图像运动过大时，在视频序列同一点上拟合曲线可能无法实现匹配，使用先验知识可以在不同点上进行拟合；

           结合金字塔，可以在较低分辨率上跟踪偏移量，在更高分辨率上使用较低分辨率结果作为初始匹配；

           在最精细分辨率下，使用迭代方式可以更加精确的跟踪光流偏移。

    在 opencv 中，使用 cv::calcOpticalFlowFarneback() 函数实现基于二次多项式拟合的稠密光流计算，其函数原型如下：

    void cv::calcOpticalFlowFarneback(cv::InputArray preImg, cv::InputArray nextImg, cv::InputOutputArray flow,

                                                          double pyrScale, int levels, int winsize, int iterations, int polyN, double polySigma, int flags);

    preImg, nextImg: 传入图像序列中前一帧与后一帧图像，图像格式均为8位单通道，且尺寸应该保持一致。

    flow: 函数记录各点运动向量，图像格式位32位浮点双通道（CV_32FC2），图像尺寸与 preImg, nextImg 保持一致。

    pyrScale: 表示金字塔各层缩减系数，一般使用 .5。

    levels: 表示金字塔层数。

    winsize: 在光流跟踪前，使用 winsize 窗口大小对图像平滑，避免噪声干扰；可将 flags 设置为 cv::OPTFLOW_FARNEBACK_GAUSSIAN 以使用 Gaussian 平滑。

    iterations: 通过控制各层上迭代拟合次数控制跟踪精度。

    polyN: 控制二次多项式拟合区间大小。

    polySigma: polyN = 5, polySigma = 1.1; polyN = 7, polySigma = 1.5。

    flags: 当使用 cv::OPTFLOW_USE_INITIAL_FLOW 时，flow 被同时当作输入参数，表示初始光流速度场；通常在序列视频中，相邻帧运动方向具有相似性，故可以使用上帧速度场作为初始猜测。

  

    参考资料： Learning Opencv 3   Adrian Kaehler & Gary Bradski

                       Robot Vision   Berthold K. P. Horn

                       Determing Optical Flow   Berthold K. P. Horn & Brian G. Schunk

                       Two-Frame Motion Estimation Based On Polynomial Expansion   Gunnar Farneback