Deformable Templates For Eye Detection

1 Abstract

    This approach was published On "Deformable Templates for Face Recognition" by Alan L. Yuille. I found that the method for eye recognition is useful for my current research, so just make notes.

    The original paper mainly described three aspects:

    1) Global templates which introduce a model that connect a set of basic features of the face by springs, the features include eyes, hair, mouth, nose, and left and right edges of the face, the method was proposed by Fischler and Elschlager. Now I am not going to focus on it.

     2) A detailed descriptions of using deformable templates to extract facial features. I am just interested in eye templates.

     3) A more robust method for deformable templates, which promises to obtain more reliable recognition. it is important for Real Application. 

 

2 Feature Template For Eye Extraction

    Suppose we want to detect eyes using traditional method. we know how to extract edges in the image, but it is hard to organize the low level edge features into a sensible global percept. The difficulty reminds me of the generalized hough transform,  but it can not describe such a sophisticated shape which has iris and white of eye. however, the deformable template can deal with it. In the deformable template approach the templates are specified by a set of parameters that enables a priori knowledge about the expected shape of the features to guide the detection process. The templates are flexible to be able to change their parameter values so as to match themselves to the data. The final values of these parameters then can be used to describe the features.

    The key idea to the deformable templates is the energy function, which gives a measure of fit of the template to the image. that is, Minimizing the energy attracts the template to salient features, such as peaks, valleys, and edges in the image. The minimum of the energy function means best(local) fit with the image. The template is first given some initial parameters which decide an initial position of the feature, then the parameter of the template is updated by steepest descent method, this correspond to following a path in parameter space(Recalling hough transform method, we sample the parameter space and then increase the space at every possible points, it is a computational cost method).

          

    By observing the above image, The template consists of the following features:

    1) A circle of radius r, centered on a point . This corresponds to the boundary between the iris and the whites of the eye and is attracted to edges in the image intensity. The interior of the circle is attracted to valleys.

    2) A bounding contour of the eye attracted to edges, which can be modeled by two parabolic sections representing the upper and lower parts of the boundary. It has a center 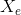, width 2b, maximum height a of the boundary above the center, maximum height c of the boundary below the center, and an angle of orientation .

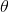    3) Two points corresponds to the centers of the whites of the eyes, which are attracted to peaks in the image intensity. These points are labeled by 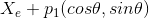 and , where 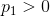 and .

    4) The regions between the bounding contour and the iris correspond to the white of the eye. They will be attracted to large value in the image intensity.

    5) 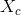 and 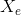 meant to be close together most of the time, but not always true.

         

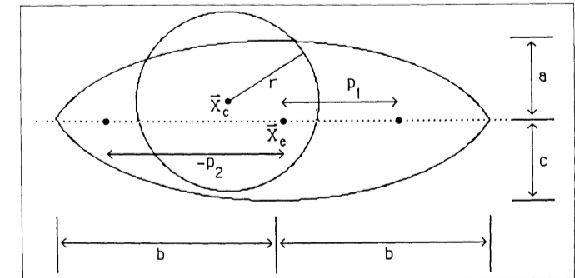
    The template is illustrated in above figure. It has a total of 9 parameters: , , 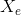, , 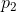r, a, b, c and 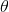.  All of these are allowed to vary during the matching.

    The parameter 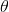rotates the template, then the parabola functions get more complicated. For simplicity, we should first reconstruct coordinate using rotation parameter, then things become simpler. We define two unit vectors as follows:

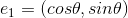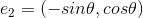    , ,  Any points x in space can be represented by  where .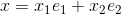

    The circle function is then defined as 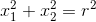, which centered at .

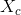    The top half of the parabola is defined as 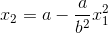, the lower half is defined as 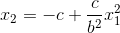, they both centered at .

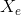    Up to now, All we need is constructing an energy function of the deformable templates. Before this, we should define some representations of the images.

    1) 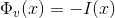, the valley of the image,  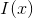 represents the image itself.

    2) 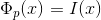, the peak of the image.

    3) , the edge of the image, the original paper use first equation, but I prefer the second one.

    These representations are chosen to extract properties of the image, such as valleys, peaks and edges. Once we have prepared these representations of the image, we can construct an energy function of the deformable templates.

    1) ,  the energy takes the minimum value over the interior of the circle.

    2) 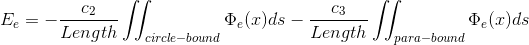, the energy takes the minimum value over the edge.

    3) 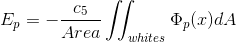, the energy takes the minimum value between the circle and the parabolas.

    4) 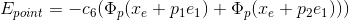, the energy takes the minimum value at two peak points in the white of eyes.

    5) 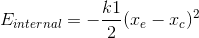, the energy takes the minimum value when two points get close together, but we should use it with caution.

    Add all of the energy function above, we get a complete energy function .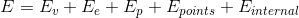

    Using the energy function, we can define an algorithm to detect the eye.

    1) Set 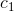 to be large enough, set other coefficients to be 0. During this epoch the valley forces pull the template to the eye(Iris).

 

    2) Increase the coefficient of the boundary of the circle 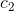. This fine tunes the size of the circle as it locks onto the iris.

    3) Increase the coefficient of the peak 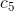. This rotates the template and get the correct orientation.

    4) Increase the coefficient of the edges of the boundary 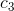. This fine tunes the position of the boundaries.

    Right now, we have only one problem not solved yet. That is, how to decide the initial values of the template parameters. Here is the strategy:

    Since the eye template might start at places where the valley representation was strong, we search in the whole image to find some local minimum in intensity. These local minimum positions may be the Initial  s. Then we should start several deformable templates off in parallel and see which gives the best results. At last we use some criteria such as the final energy function to decide which one is the best. However, the criteria may fail sometime, so we should check the template parameters meanwhile to avoid making mistake. Generally, if we come across a group of template parameters that are extremely unlikely, we should discard them even if the energy function is minimum.

 

3 Robust Feature Templates

    The method described in the previous section may fail in several situations, such as partial occlusion or noise.

        

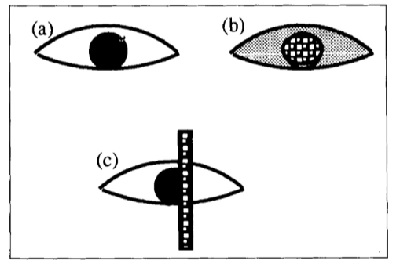
    Consider the problem of estimating the mean from a set of samples .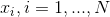 

    The sample mean is 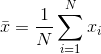,  and the least square error is .

    The sample mean is extremely sensitive to outliers. A robust technique for estimating the mean should be relatively independent of such outliers and should also enable us to identify the outliers themselves. We can use least trimmed squares to achieve the goal. For each value of x we order the residuals 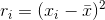 so that 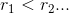, we choose M(M < N) points that has less residuals, then use these points to calculate the mean and least square error.

    We can use the above idea to reformulate the deformable templates algorithm. The geometry model keep same as before. The measures of fit aim to find the parameters of the template that minimize the mean in the iris region, maximize the mean for the whites of the eyes, and maximize the mean edge strength at the boundaries. We order each variables by residuals, and then just use portion of them for the energy function. This give us better effect when partial occlusion or noise.

 

4 References

    Alan L. Yuille. Deformable Templates for Face Recognition.