最小二乘法

一 常规最小二乘法拟合直线

    1 分析方法

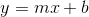     已知数据点为 ，欲拟合直线 ，则有最小化：。

              

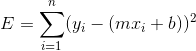    使用矩阵表示，令 ，则有：,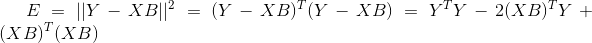

    X, Y已知，要使E最小化，则向量B求导等于零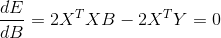：，整理得：。

    2 线性代数方法

    在分析方法中，使用最小误差法拟合直线。这里还可以使用线性代数中正交原理得到相同结果。

    1）线到线上投影

         

    如上图所示，b 到 a 的投影为 p = xa，由于 e 与 a 垂直，有 (b - xa)a = 0，未知数为 x。

    求解方程得 ，。

    带入 x 值，计算出 b 到 a 的投影为 ，投影矩阵为 ，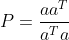

    根据投影矩阵，b 到 a 的投影可重写为 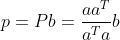。给定一个向量，可以求解出投影到该向量的投影矩阵，任意向量到给定向量的投影即为 Pb 。

    2）线到面上投影

        

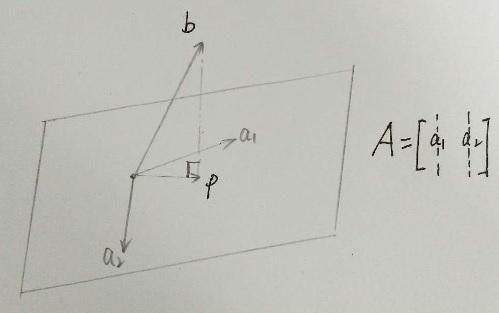
    如上图所示，超平面为矩阵 A 的列空间构成（为了可视化，上图限制为二维平面，但结论对 N 维平面均适用），b 到平面 A 的投影为 p ，p 可表示为 。

    类似线到线投影，e = b - p，e 垂直于平面 A，有：

    ，，。

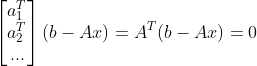    带入 x 计算出 b 到平面 A 的投影为 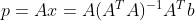，投影矩阵为 。

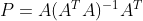    根据投影矩阵， b 到平面 A 的投影可重写为 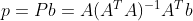。给定一个矩阵，可以求解出投影到该矩阵列空间构成的超平面上的投影矩阵，任意向量到给定矩阵列空间构成的超平面上的投影为 Pb。

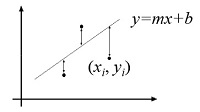
    3）直线拟合

    设直线方程为 y = kx + b，对于任意点 (x,y)，带入直线方程得：

    ，当向量 落在矩阵 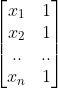 列空间构成得超平面外时，方程组无解。这也正是最小二乘法需要解决得问题。

   将向量  投影到矩阵 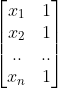 列空间构成的超平面，根据线到面上投影，可以寻找投影向量 p，改写方程为 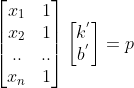，该方程组有解。

   使用 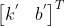作为原方程的最佳近似解，带入 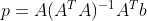，解得 。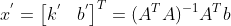

   对于方程组 Ax=b，当 b 不在矩阵 A 的列空间时，无法求得 x 精确解，但可以求得 x 的近似解，使得 。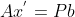

   实际运算中，并不需要特意求解 P，只需对方程组做如下变换即可：

   。

 

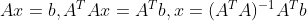二 使用垂直距离改写E

    常规最小二乘法有如下问题：

    1）数据点旋转后，求解得直线是变化的；

    2）垂直直线无法求解；

    通过修改 E 表达式，可以克服以上问题，如下图：

                  

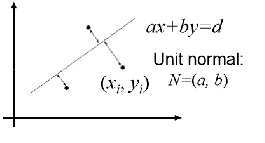
    假设 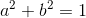，图中直线方程  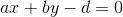已经归一化，任意点 到直线的距离为 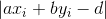，则有最小化：。

    上式中，a,b,d 均为未知量，首先对求偏导，有：，整理得：，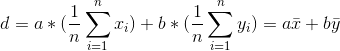

    将d代入E中得：。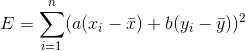

    使用矩阵表示，令 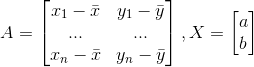，有： ，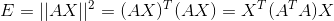

    对X求导，可得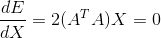：，求解二元一次方程组  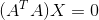可计算处拟合直线。

 

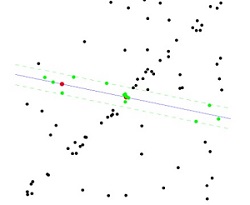
三 RANSAC(Random Sample Consensus)

     

    如上图所示，少数离群点可使拟合出现较大偏差。因此，应该使用一些逻辑来降低离群点干扰，具体措施如下：

    1）随机选取一个子集，使用最小二乘法拟合直线；

    2）在规定得误差范围内计算合群点；

    3）多次选取不同的子集，继续1）2）操作；

    4）选择合群点最多模型作为拟合初步结果，使用该模型下所有合群点重新拟合直线，得到最终结果。