Blob检测
一 Laplace 算子
使用一阶微分算子可以检测图像边缘。对于剧烈变化的图像边缘，一阶微分效果比较理想。但对于缓慢变化的图像边缘，通过对二阶微分并寻找过零点可以很精确的定位边缘中心。二阶微分即为 Laplace 算子，在 "图像边缘检测" 中进行的推导。以一维图像为例，下图给出边缘的一阶与二阶运算结果：
红色区曲线表示原始边缘，绿色曲线表示一阶微分结果，蓝色区域表示二级微分结果。
如何使用 Laplace 算子检测到图像边缘呢？其基本方法如下：
1）使用 Laplace 算子与图像卷积；
2）在邻域(3*3, 5*5, 7*7等)中寻找卷积后最大值与最小值；
3）当最大值大于0，最小值小于0，最大值大于某固定阈值，最小值小于某固定阈值的负值时认为找到边缘(避免噪声干扰)；
二 Laplacian of Gaussian(LoG)
Laplace 算子检测边缘同时也检测到噪声，可以首先使用 Gaussian Kernel 对图像去噪，然后在去噪后图像上应用 Laplace 算子。
由于线性运算可结合性质，有如下结论：
；
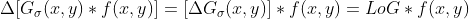以下给出证明：
；
。
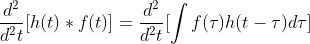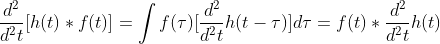根据以上结论，由于 Gaussian Kernel 在卷积运算前已知且相对固定，可以先对求解 LoG，然后再使用 LoG 对图像卷积。
；
；
；
。
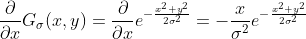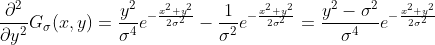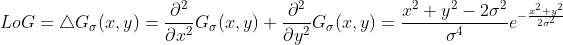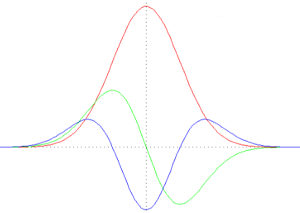
上图给出一维高斯函数的一阶微分（绿色）与二阶微分（蓝色）。
通过离散化近似处理，可以得到 LoG 核模板(5*5)，
，使用该模板检测图像边缘，步骤如下：
1）计算 LoG 核；
2）使用 LoG 核与图像卷积；
3）在5*5邻域中寻找卷积后最大值与最小值；
4）当最大值大于0，最小值小于0，最大值大于某固定阈值，最小值小于某固定阈值的负值时认为找到边缘；
三 Difference of Gaussian(DoG)
使用 DoG 可以得到与 LoG 近似的效果，步骤如下：
1）使用宽度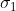 
高斯核与原图像卷积
；
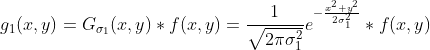2）使用宽度 
高斯核与原图像卷积
；
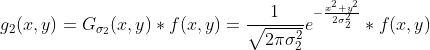3）求两卷积之差
；
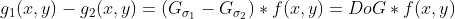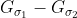可以提前计算出来 
；
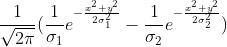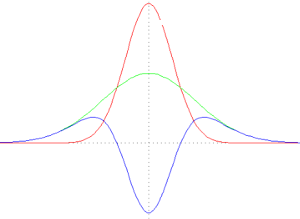
上图给出两个不同宽度的一维高斯函数的一阶微分（红色与绿色）与DoG（蓝色），观察发现 DoG 与 LoG 形状基本一致，所有可以使用 DoG 求二阶过零点。
四 Blob检测
使用 LoG 可以检测函数过零点，以一维图像为例，如下图：
对不同尺寸Blob块使用 LoG ，可得如下结果：
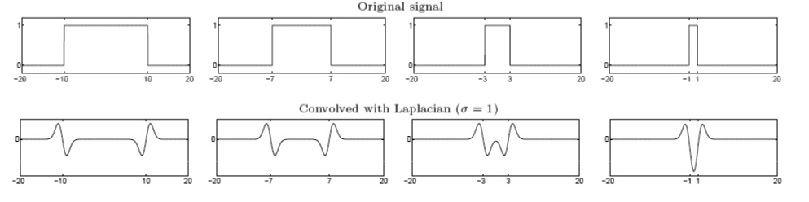
由上图可知，对于不同尺寸Blob块，二阶微分响应不同。当Gaussian函数尺度与Blob块直径基本一致时，产生最大响应。
对于一个固定尺寸Blob块，使用不同尺度Gaussian函数时，响应如下：
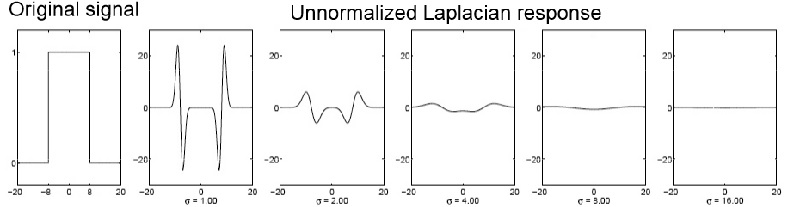
Laplacian 响应随着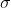 
增大而减小，需要对对响应值进行归一化处理。
高斯函数的一阶微分对理想阶跃边缘的响应随着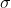 
增大而降低，在一阶微分卷积前乘以 
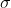以归一化响应，在二阶微分卷积前乘以 
以归一化响应。
以下给出二维归一化 LoG 表达式：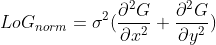
。
使用不同尺度归一化Gassian二阶微分，响应如下：
通过以上图像可知，当Gassian函数尺度与Blob块直径基本一致时，产生最大响应。
通过以上观察，可得到Blob块检测方法：
1）使用不同尺度Gassian函数的归一化二阶梯度分别于图像卷积；
2）合并不同尺度下卷积图像形成三维图像；
3）在三维图像中寻找局部极大值，该极大值即为检测到的Blob块，其中Blob块中心由所在图像坐标决定，Blob块半径由所在尺度决定，其值为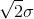 
。
五 Blob 特征点描述
当检测到特征点后，使用自相关函数可以描述 Blob 特征点形状特征：
；
令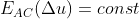 
，在 uv 平面上可以得到一个椭圆，如下：
观察椭圆可知，在短轴方向上 Blob 特征点变化速度最快，在长轴方向上变化最慢。同时，自相关矩阵描述了特征点形状及旋转关系。
当采集图像发生了射影变换（旋转，拉伸），其 Blob 特征点的自相关矩阵所描述的椭圆也会发生 旋转，拉伸变换。在描述 Blob 特征点前，首先对其进行拉伸变化将椭圆转换为正圆，这样方便对特征点进行统一描述。
以上操作使特征点具有相同的拉伸变换，但仍旧需要使特征点具有统一的旋转角度，使用梯度方向直方图可以估计特征点旋转。具体如下：
1）使用特征点周边固定区域内的梯度方向形成方向直方图；
2）使用直方图中最大 bin 作为特征点方向（零点方向）；
3）在 Blob 区域内（正圆，去除拉伸）统计方向直方图，该直方图可作为特征描述符。
参考： https://www.cs.unc.edu/~lazebnik/spring11/lec08_blob.pdf
