机械设计基础2-3
平面连杆机构
平面连杆机构
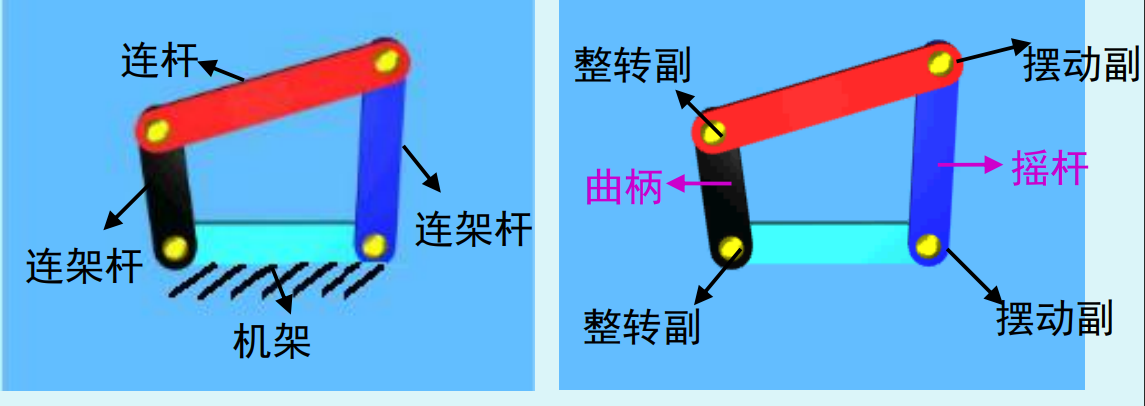
全部用转动副链接的平面四杆机构称作平面铰链四杆机构。下面我们区分几个概念:
机架: 固定不动的构件
连架杆: 与机架相连的两个构件
连杆: 连接两个连架杆的构件
整转副: 两构件能作整周相对转动的转动副
摆动副: 两构件不能作整周相对转动的转动副
摇杆: 与机架组成摆动副的连架杆
曲柄: 与机架组成整转副的连架杆
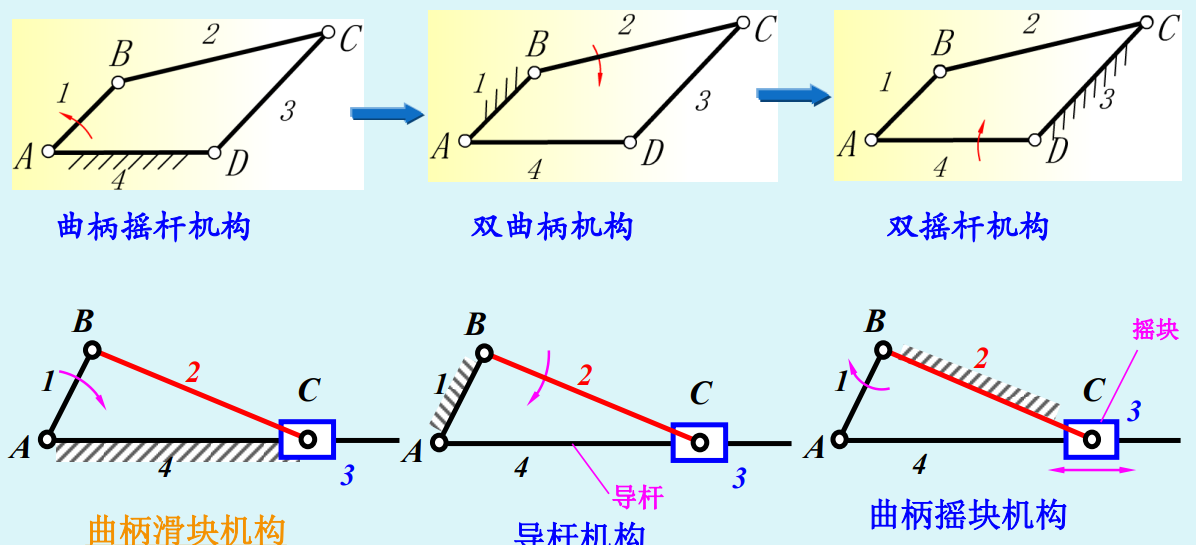
按照分类,常见的可以分为曲柄摇杆机构,双曲柄,双摇杆,等等等等。
下面介绍其演化型式,加入若干移动副,移动副可认为是回转中心在无穷远处的转动副演化而来。

曲柄滑块
去掉一个连架杆,不改变运动轨迹,叫做曲线导轨曲柄滑块机构
然后设这个摇杆半径无穷大,就得到 偏置曲柄滑块
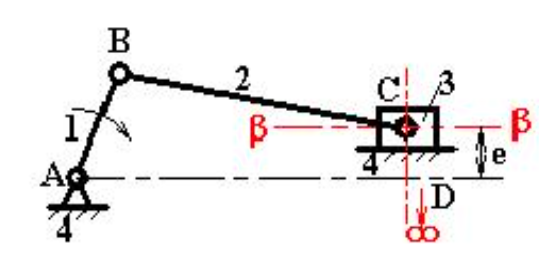
对心曲柄滑块(偏距\(e=0\))

下面我们讨论其存在曲柄的条件
显然BC不能为曲柄,只能AB。也就是A是回转副,最短杆在AB

所以
偏置曲柄滑块机构有曲柄存在条件:\(a+e\le b\),且最短杆为连架杆。
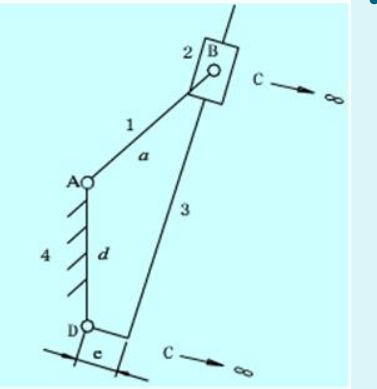
导杆
将连杆及其连接的两个转动副换成一个转动副和一个移动副
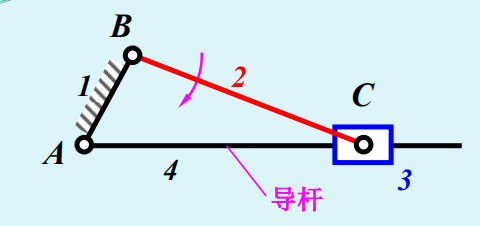
存在曲柄的条件
A为回转副,AB为最小杆,\(d+e<=a\),证明同上,略
机构的倒置
机构的倒置:选运动链中不同的构件作机架以获得不同机构的演化方法称为机构的倒置
平面四杆机构的基本特性

铰链四杆机构中曲柄存在的条件
上文已说
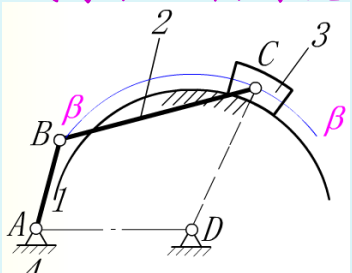
急回运动特性
当机构的原动件匀速连续回转时,从动件往复运动平均速度不等的性质。这可以节省空回时间,提高生产效率。
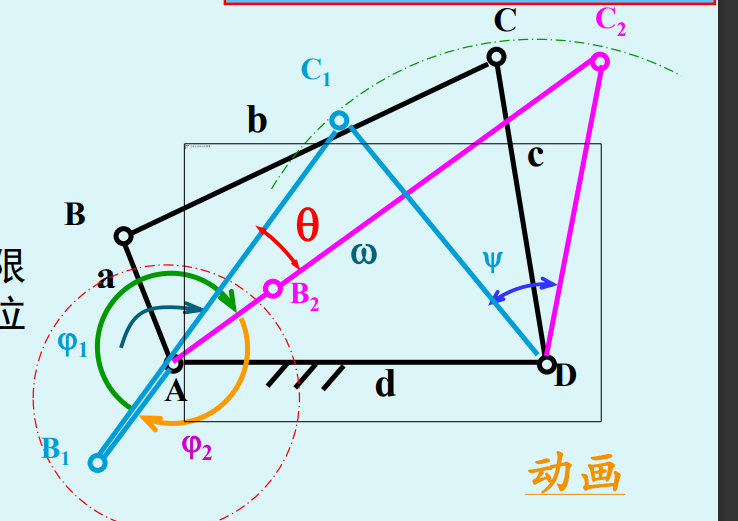
极位 曲柄与连杆两次共线时,从动件所处的两个极限位置。
摆角 从动件摇杆两极限位置的夹角\(\psi\)。
极位夹角 对应从动杆的两个极限位置, 主动件两相应位置所夹角\(\theta\) \(\theta \in[0,180)\)
其存在急回运动特性的本质特性是因为\(\theta\)存在。并且急回特性具有方向性。
从动件快行程平均速度与慢行程平均速度的比值称为从动件行程速度变化系数,用K表示。注意\(C_1C_2\)表示的是弧。
并且同时可以算出
压力角和传动角
压力角\(\alpha\)
从动件(运动输出件)受力点的力作用线与该点速度方向线所夹锐角. (不考虑摩擦) 用\(\alpha\)表示。

传动角\(\gamma\)
压力角的余角,用\(\gamma\)表示,也可以表示成连杆轴线与从动连架杆轴线所夹锐角。
一般机械,常取\(\gamma \ge 40^o\);对于鄂式破碎机、冲床等大功率机械,最小传动角应取大一些,可取\(\gamma \ge 50^o\);对于小功率的控制机构和仪表,则可略小于40.
曲柄摇杆机构,当曲柄主动时,在曲柄与机架共线的两个位置之一,传动角最小。
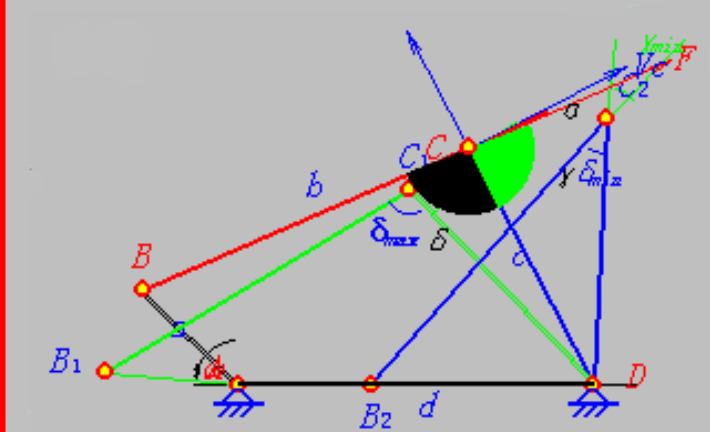
在下图中,连杆近似无穷远

死点
从动件的传动角等于0时,机构的位置为死点位置。此时机构顶死或运动不确定。一个一个找就行

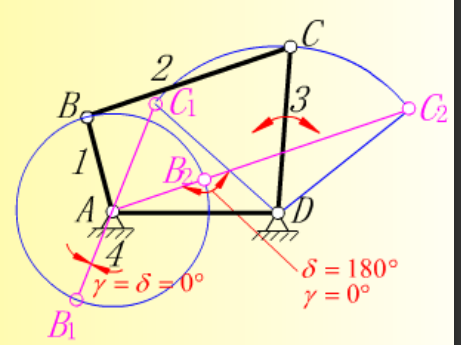
转向点

克服死点
利用相同机构错位排列的方法,或者从动件安装飞轮利用惯性。
凸轮
一、组成及应用和分类
组成
凸轮是一个具有曲线轮廓或凹槽的构件。凸轮通常作等速转动,但也有作往复摆动或移动的。从动件是被凸轮直接推动的构件。凸轮机构就是由凸轮、从动件和机架三个主要构件所组成的高副机构。其定义如下
凸轮——具有曲线轮廓或凹槽的构件。
从动件——被凸轮直接推动的构件。
机架——相对参照系
应用
略
分类
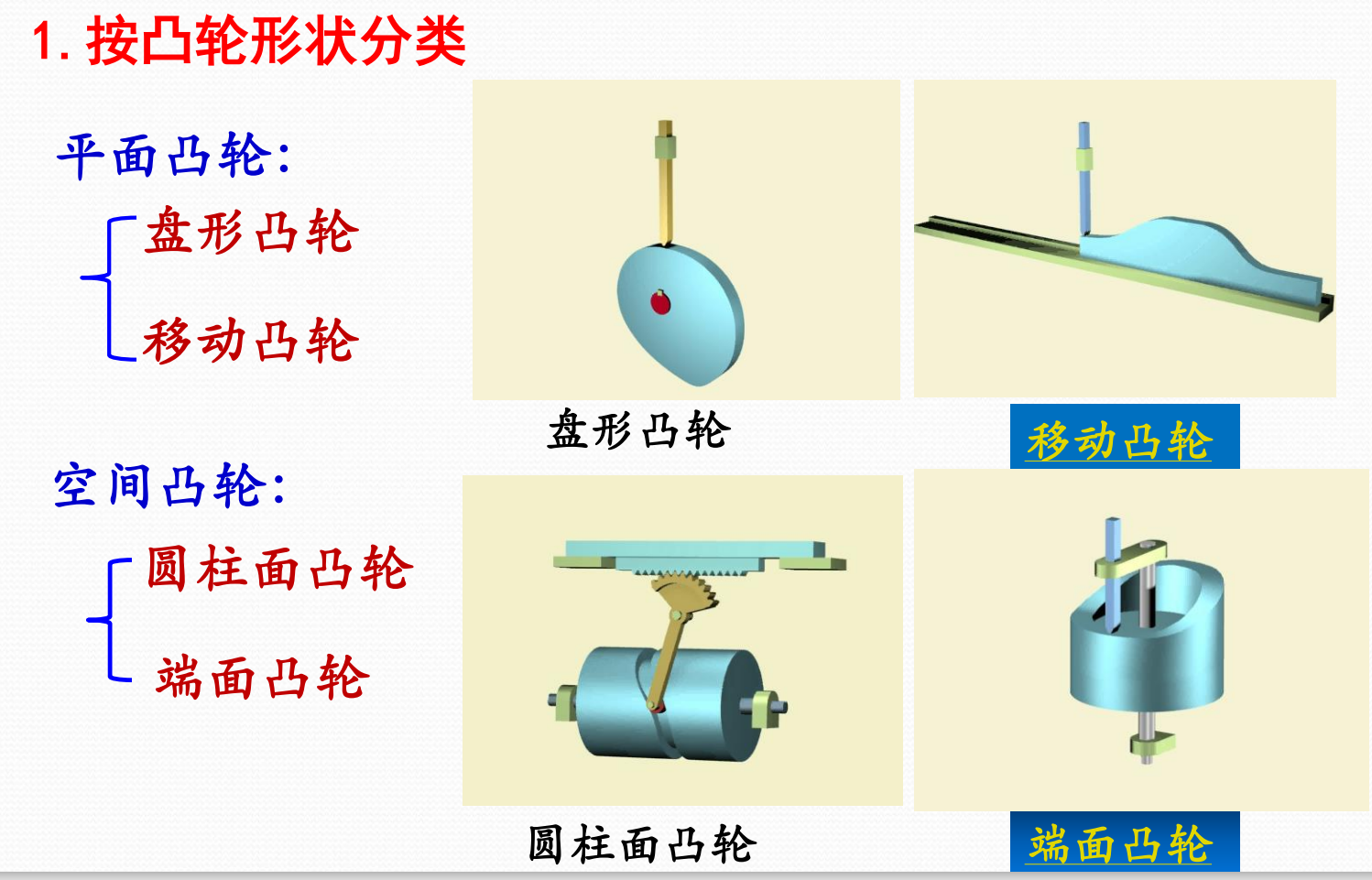
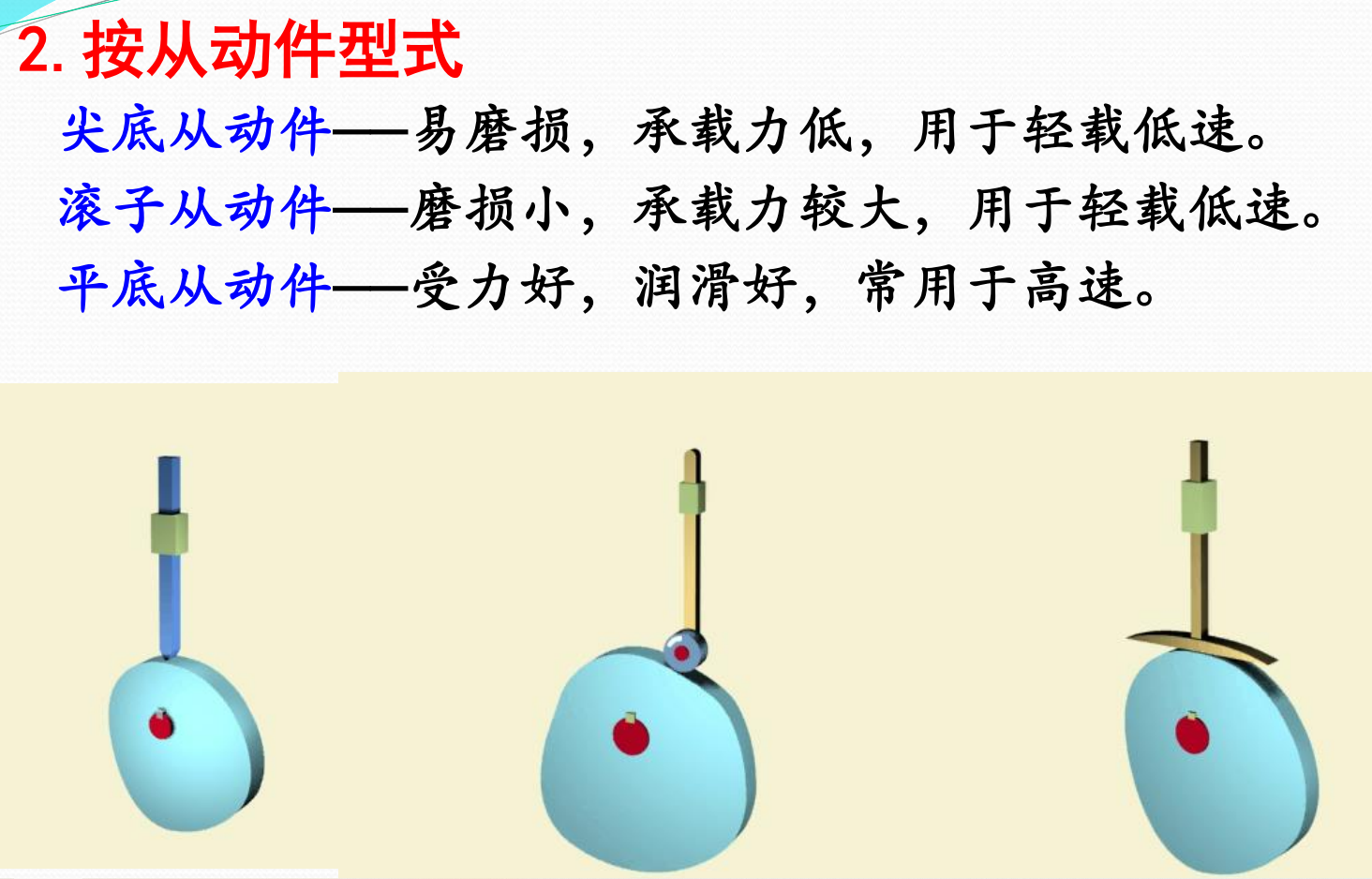
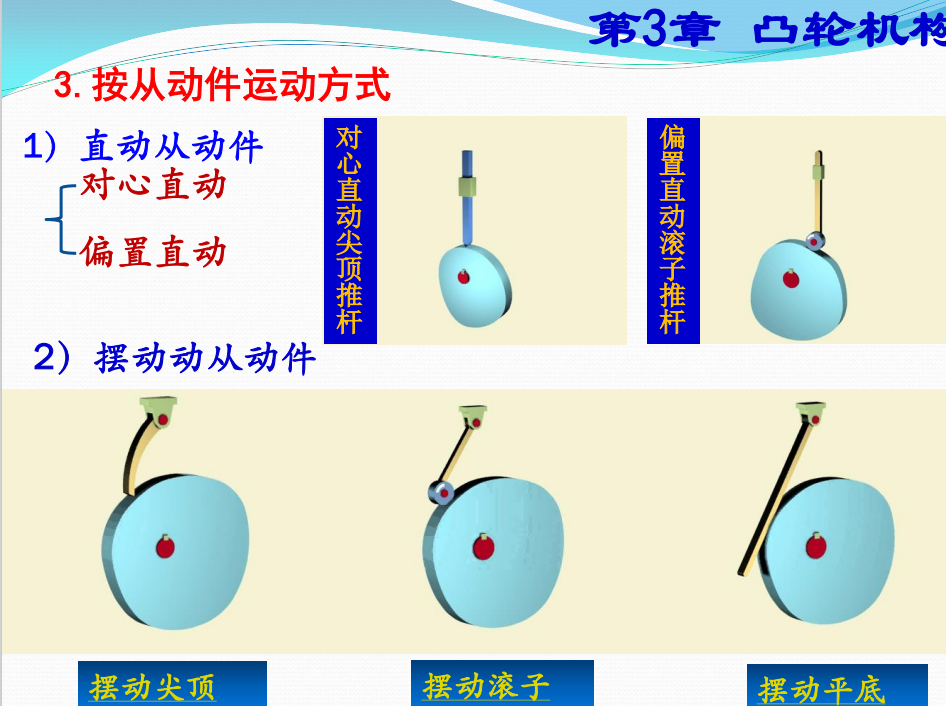
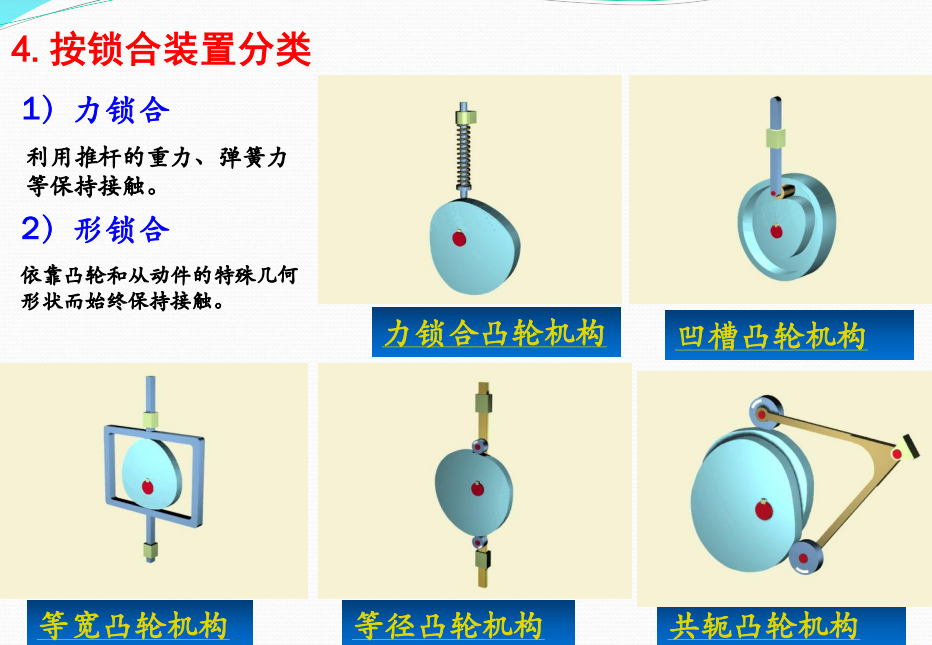
How to name it
凸轮机构的命名:3+2+1

各种参数

反转法
1.反转法:给整个凸轮机构施以\(-omega\),凸轮静止,从动件尖顶复合运动的轨迹即凸轮的轮廓曲线。
重点掌握导路怎么找
引用
源: 与必应的对话, 2023/3/26(1) 曲柄滑块机构_百度百科. https://bing.com/search?q=如何判断一个导杆是转动导杆机构还是摆动导杆机构 访问时间 2023/3/26.
(2) 满足转动导杆机构的条件是什么_百度知道. https://zhidao.baidu.com/question/945541267653619252.html 访问时间 2023/3/26.
(3) 满足摆动导杆机构的条件是什么_百度知道. https://zhidao.baidu.com/question/561539903262441052.html 访问时间 2023/3/26.
(4) 曲柄滑块机构_百度百科. https://baike.baidu.com/item/曲柄滑块机构/10861282 访问时间 2023/3/26.
(5) 摆动导杆机构的压力角为啥是0? - 知乎. https://www.zhihu.com/question/57078867 访问时间 2023/3/26.
(6) 摆动导杆原理动画 - 知乎. https://zhuanlan.zhihu.com/p/138193156 访问时间 2023/3/26.

