工程光学

1 平面镜

它是唯一能够成完善像^[1]的光学元件。并且对于平面镜有

\[r=-\infty \quad n'=-n \tag{1.1.1} \]

这里也可以类比以下以前的公式

• 球面物像公式\(\displaystyle \frac{n'}{l'}-\frac{n}{l}=\frac{n-n'}{r}\)
• 球面反射公式\(\hspace{0.2cm} n'=-n\hspace{0.2cm}\) \(\displaystyle \frac{1}{l'}+\frac{1}{l}=\frac{2}{r}\)

代入之前我们的像物距和放大率公式，可得

\[\begin{align} \frac{1}{l'}+\frac{1}{l}&=0\implies l=-l' \tag{1.1.2.a}\\ \beta=\frac{n'l}{nl'}&=1 \tag{1.1.2.b} \end{align}\]

从上两式，我们可以很显然看出，平面镜成正立等大虚实相反像。

1.1 成像

成像特征

对于镜像，奇次反射，右手坐标系变左手坐标系。如图所示

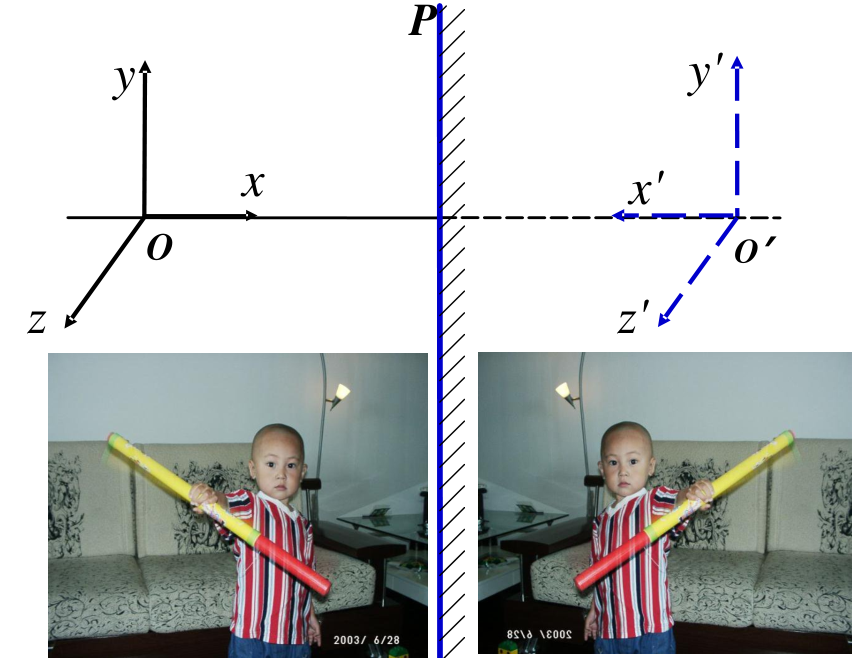
规律总结如下

\[\left\{ \begin{align*} 奇次反射：&成镜像，右手坐标变为 左手坐标；\\ 偶次反射：&成相似像，坐标方向不 变。虚实相反。 \end{align*}\right.\]

平面镜旋转特性

假如入射光线方向不变，我们将平面镜旋转\(\alpha\) 角度，则出射光线旋转\(2\alpha\)角度（以顺时针旋转为正方向）

等效于入射光线先增大\(\alpha\)，然后再旋转\alpha$，所及就有\(2 \alpha\)

光杠杆

2 双平面镜系统

双平面镜反射

\[\begin{align} \alpha&=I''-I_2 \tag{1.3.1}\\ \beta&=2I''-2I_2=2\alpha \tag{1.3.2} \end{align}\]

如图所示

双平面镜连续成像

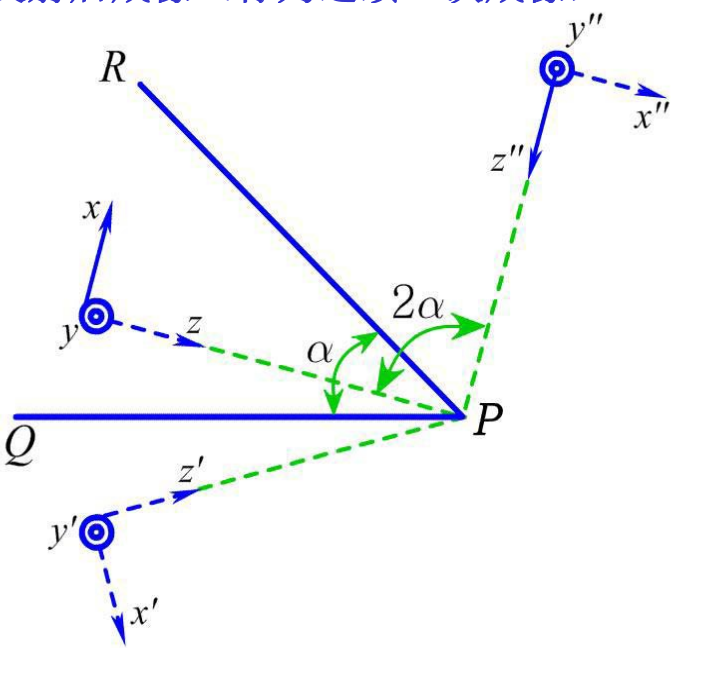
坐标系相同，成一致像。可认为是由物体绕棱边旋转\(2\alpha\)角形成的， 其转向与光线在反射面的反射次序所形成的转向一致。

3 平行平板折射

平行平板是由两个相互平行的折射平面构成的光学元件。
平行平板是光学仪器中应用较多的一类光学元件，如
分划板、 盖玻片、 滤波片

成像特征

①平行平板折射后方向不���

用折射公式（两平板之间折射率为\(n\)）

\[\begin{align} \sin I_1=n\sin I_1'&=n \sin I_2=\sin I_2' \tag{1.3.1.a}\\ I_1&=I_2' \tag{1.3.1.b} \\ U_1&=U_2 \tag{1.3.1.c} \end{align}\]

② 平行平板无光焦度

平行平板不会使物体放大或缩小， 是个无光焦度元件，
在系统中对光焦度无贡献

\[\alpha=\beta=\gamma=1 \tag{1.3.2} \]

③ 侧向位移\(\Delta L=DG\)

TODO: \(DG\neq EF\)?

\[\begin{aligned} DG&= DE \sin \angle DEG=DE \sin (I_1-I_1') \hspace{0.3cm} (延长A'D)\\ &=\frac{d}{\cos I_1'} \sin (I_1-I_1')\\ &=\frac{d}{\cos I_1'} (\sin I_1 \cos I_1'-\sin I_1'\cos I_1)\\ &=d \sin I_1\left( 1-\frac{\tan I_1'}{\tan I_1}\right)\\ &=d \sin I_1\left( 1-\frac{\cos I_1}{n\cos I_1'}\right) \end{aligned} \tag{1.3.3}\]

④ 轴向位移\(\Delta L'\)

\[\begin{aligned} \Delta L'&=\frac{\Delta L}{\sin U_1}=\frac{\Delta L}{\sin I_1}\\ &=d \left( 1-\frac{\tan I_1'}{\tan I_1}\right)\\ &=d \left( 1-\frac{\cos I_1}{n\cos I_1'}\right) \end{aligned} \tag{1.3.4}\]

轴向位移随入射角而变，即轴上点物\(A_1\)不成点像,平行平板不能成完善像。

⑤平行平板的位移成像——像的位置

平行平板的等效光学系统

近轴区成像（入射角很小时）

\[\begin{align} \cos I_1 &\thickapprox \cos I_1'=1 \tag{1.3.5} \\ \Delta L'&=d(1-\frac{1}{n}) \tag{1.3.6} \end{align}\]

此时点物成点像，平行平板在近轴区以细光束成像是完善的。

等效空气平板

并不是完全相等的！是“等效”的一个概念，因此我们在计算平行平板的光学系统时候，将其简化成等效空气层，最后再沿光轴移动一个轴向位移。
等效空气平板的厚度为

\[\overline{d} =d-\Delta L'=d-d(1-\frac{1}{n})= \frac{d}{n} \tag{1.3.7} \]

反射棱镜

一个或多个反射面磨制在同一个棱镜上的光学元件，称为反射棱镜。

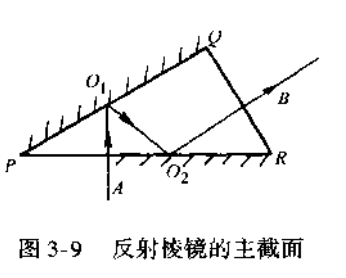
光轴：光学系统的光轴在棱镜中的部分称为棱镜的光轴，一般为折线，如图3-9中的\(AO_1,O_1O_2\)
和\(O_2B\)。每经过一次反射，光轴就折转一次。

入射面和出射面：反射棱镜的工作面为两个折射面和若干个反射面，光线从一个折射面入射，从另一个折射面出射，因此，两个折射面分别称为入射面和出射面，大部分反射棱镜的入射面和出射面都与光轴垂直。

棱：工作面之间的交线称为棱镜的棱

主截面：垂直于棱的平面叫主截面
光轴截面：在光路中，所取主截面与光学系统的光轴重合，因此又叫光轴截面。

反射棱镜大体上分为简单棱镜、屋脊棱镜、立方角锥棱镜和复合棱境四类，下面分别予以介绍。

(一)简单棱镜

简单棱镜只有一个主截面，它所有的工作面都与主截面垂直。根据反射面数的不同，又分为一次反射棱镜、二次反射棱镜和二次反射棱镜。

一次反射棱镜

上图中的a,b,c分别为等腰直角棱镜【\(\angle 90^o\)】，等腰梯形棱镜【\(\angle r^o\)】和道威棱镜（等腰直角棱镜去掉不必要的直角部分）。并且经过反射，右手坐标系会变成左手坐标系。

道威棱镜的重要特性之一是，当其绕光轴旋转\(\alpha\)角时，反射像(或者说，坐标系)同方向旋转\(2\alpha\)角。如上图(c)中的第二个图可以看出是道格棱镜垂直纸面向内旋转90度，像坐标系垂直纸面向里旋转180度。
如下的周视瞄准仪^[1:1]就利用了这一特征。

因为我们想要始终得到正立的像，垂直纸面向里旋转上方棱镜\(2 \alpha\)度，就要反方向旋转道威棱镜$ \alpha$度。

二次反射棱镜

偶次成像，没有镜像。

三次反射棱镜

光路很长，可以折叠光路，使仪器紧凑。

屋脊棱镜

用交线位于棱镜光轴面内的两个相互垂直的反射面取代原来的反射面，使垂直于主截面的坐标被这二个
相互垂直的反射画依次反射。
这两个相互垂直的反射面叫做屋脊面，带有屋脊面的棱镜称为屋脊棱镜。

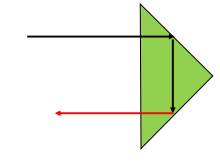
作用： 实现倒像功能，使像相对于物转过180° 同时还是右手坐标系

折射棱镜

忻射棱镜是通过两个折射表面对光线的折射进行工作的，两折射面的交线称为折射棱，两折射面间的二面角
\(\alpha\)称为折射棱镜的折射角。同样，垂直于折射棱的平面称为折射棱镜的主截面。

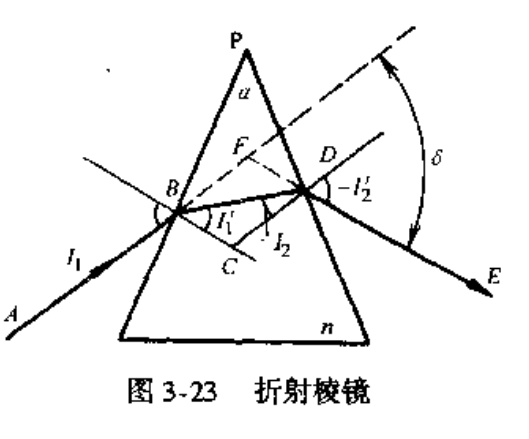
注意一下图中是\(-I_2\)

1、折射棱镜的偏转

如图3-23所示，光线AB入射到折射棱镜P上，经两折射面入的折射，出射光线DE与射光线AB的夹角\(\delta\)称为偏向角，其正负规定为：由入转出，顺正逆负。下面进行公式推导：

首先使用两次折射公式

\[\begin{align} \sin I_1&=n'\sin I_1' \tag{2.1.1.a}\\ \sin I_2'&=n'\sin I_2 \tag{2.1.1.b} \end{align}\]

同时有

\[\begin{align*} \delta&=\angle FDB+ \angle FBD \\ &=I_1-I_1'+[(-I_2')+I_2] \tag{2.1.2} \end{align*}\]

继续在四边形PBCD 中，

\[\alpha+\angle BCD=180^o=I_1'-I_2+\angle BCD\tag{2.1.3} \]

显然将(2.1.3)代入(2.1.2)中，可得

\[\delta=I_1-I_2'-\alpha \tag{2.1.4} \]

也就是

\[\delta+\alpha=I_1-I_2' \tag{2.1.5} \]

我们通过式(2.1.1.a)减去(2.1.1.b)，再用和差化积求解出\(\sin(I_1-I_2')\),设\(\displaystyle i_1=\frac{I_1+I_2'}{2} \hspace{0.3cm} i_2=\frac{I_1-I_2'}{2} \hspace{0.3cm} i_1'=\frac{I_1'+I_2}{2} \hspace{0.3cm} i_2'=\frac{I_1'-I_2}{2}\)，可得

\[\sin i_2 \cos i_1=\sin i_2' \cos i_1' \tag{2.1.6} \]

将(2.1.5)代入，得

\[\begin{align*} \sin \frac{\delta+\alpha}{2}=\sin i_2&=n'\sin i_2'\frac{\cos i_1'}{\cos i_1}\\ &=n'\sin \frac{\alpha}{2} \frac{\cos \frac{I_1'+I_2}{2}}{cos \frac{I_1+I_2'}{2}} \end{align*} \tag{2.1.7}\]

2、最小偏角

对(2.1.5)两边对\(I_1\)求偏导，得

\[\frac{\mathrm{d}{\delta}}{\mathrm{d}{I_1}}=1-\frac{\mathrm{d}{I_2'}}{\mathrm{d}{I_1}}\tag{2.1.8} \]

对(2.1.1)两边对\(I_1\)求偏导，并且等式两边同乘\(\mathrm{d}{I_1}\),得

\[\begin{align} \cos I_1 \mathrm{d}{I_1}&=n'\cos I_1' \mathrm{d}{I_1'}\tag{2.1.9.a}\\ \cos I_2' \mathrm{d}{I_2'}&=n'\cos I_2 \mathrm{d}{I_2} \tag{2.1.9.b} \end{align}\]

对(2.1.3)两边对\(I_1\)求偏导,得\(\mathrm{d}{I_1'}=\mathrm{d}{I_2}\),将(2.1.9)两式相除，得

\[\frac{\mathrm{d}{I_2'}}{\mathrm{d}{I_1}}=\frac{\cos I_1' \cos I_2'}{\cos I_1 \cos I_2} \tag{2.1.10} \]

根据折射定律

如果\(\delta\)要取最小，(2.1.10)=1,再根据折射定律，可得联立方程组

\[\begin{align*} \frac{\sin I_1}{\sin I_1'}&=\frac{\sin I_2'}{\sin I_2}=n \tag{2.1.11.a}\\ \frac{\cos I_1}{\cos I_1'}&=\frac{\cos I_2'}{\cos I_2} \end{align*} \]

这里带入\(I_1+I_2'=0,I_1+I_2'=0\)

TODO: WHY NOT =<

代入(2.1.7)可得最小偏向角

\[\sin \frac{\delta+\alpha}{2}=n' \sin \frac{\alpha}{2} \tag{2.1.12} \]

3、色散现象

长波长的色光折射率低，短波长的色光折射高。

红光波长760~622纳米，折射率低，偏向角小。紫光波长低，折射率高，偏向角大。

一些定理

棱镜转动定理

附录

参考链接

• https://zhidao.baidu.com/question/1833157291350784140.html

• 周视瞄准镜 https://wenku.baidu.com/view/e5eb94c0915f804d2a16c117.html?wkts=1679381588808

foot note

---

1. 周视瞄准仪是一种光学系统，可以让观察者在目镜不动的情况下，360度旋转物镜观察周围的环境¹²。它由直角棱镜和道威棱镜组成，利用折射和反射的原理实现水平周视和俯仰观察⁴。它广泛应用于一些需要精确瞄准和定位的仪器和机器，如坦克、火炮等¹²⁵⁶。 ↩︎ ↩︎