互感电路
互感(mutual inductance)
自感(self-inductance)

- The change in current produces a change in magnetic field(磁场), which in turn creates an induced(感应的) voltage.
- 当电压的正极是电流流入的的方向的时候,有(这时候跟绕向无关,具体见下解析)
\[U=L \frac{\mathrm{d}{i}}{\mathrm{d}{t}} \]
为什么跟绕向无关
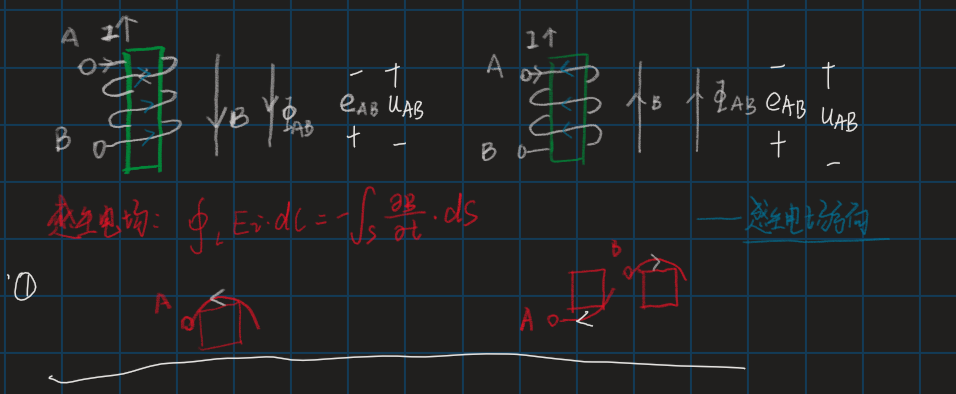
这里一开始我之所以困惑是因为没有深刻理解了法拉第电磁感应定律,其感应电压方向的确定方法,下面介绍两种方法。
- 使用楞次定律,产生电压的方向一定会阻碍原来磁通量的增加
- 或者使用由楞次定律推导出的感生电场的公式(磁场增加的反方向和感生电场成右手螺旋关系)
\[\int _ { L } E _ { i } \cdot d I = - \int _ { S } \frac { \partial B } { \partial t } \cdot d S
\]
互感(mutual inductance)
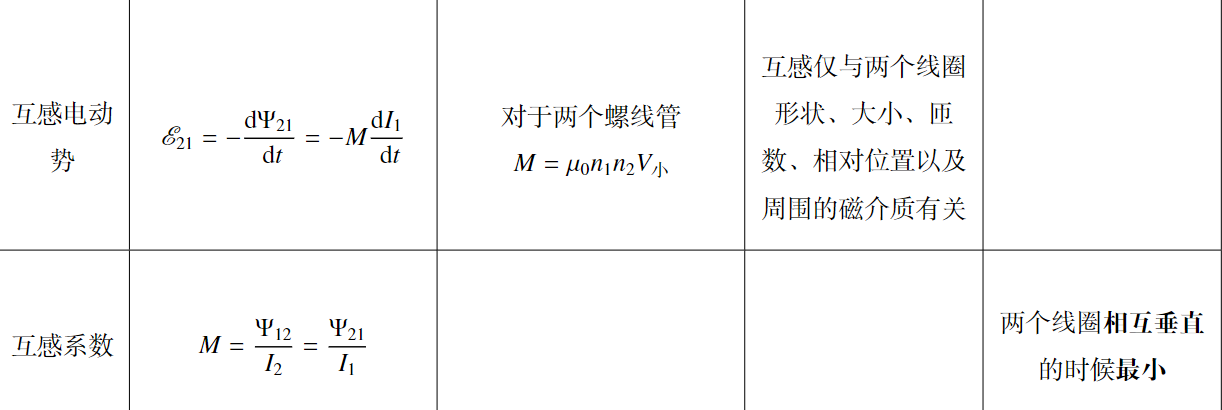
耦合系数
\[k=\frac{M}{\sqrt{L_1L_2}}
\]
同名端
为什么要定理同名端呢?见下图
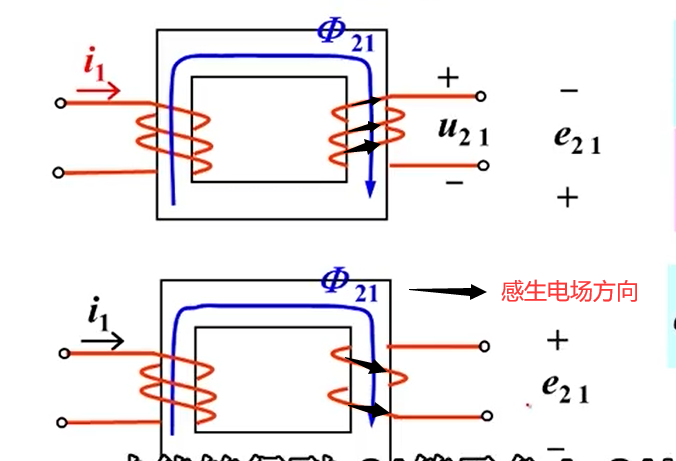
其中右端仅仅改变了绕向,产生的互感电压方向就发生了改变,与之前的自感线圈的绕向不会影响其电压方向不同。
我们定义同名端为(官方为第一种概念,第二种是我自己推导出来的):
- 当电流通过同名端其一接线端流入时(与线圈缠绕方式有关),在另一个接线端产生的互感磁通相互加强。
- 选定双端网络的任意一个接线端,与在另外一个电感产生的感应电场流向的(感生电动势为正的)接线端。
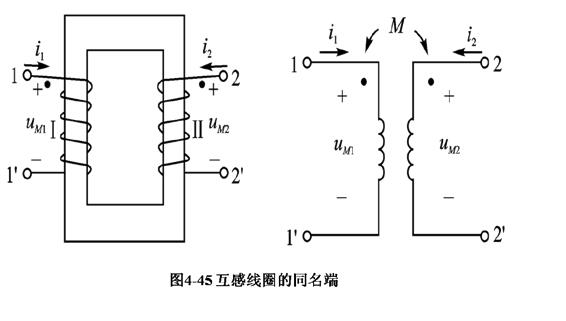

- 同时,
标准情况下一定是电流流入的地方是电压的正电位,这是基于我们之前讨论的自感电压的参考方向。 - 使用替代定理,我们仅分析一端有激励的时候,电路从一端的同名接线端流入,感生出的电压的正极在另一同名端,这与之前的定义相吻合。
关系
根据元件的KVK列出
\[\begin{bmatrix}
u_1 \\
u_2
\end{bmatrix}=\begin{bmatrix}
L_1&\pm M \\
\pm M&L_2
\end{bmatrix}\begin{bmatrix}
\frac{\mathrm{d}i_1}{\mathrm{d}t} \\
\frac{\mathrm{d}i_2}{\mathrm{d}t}
\end{bmatrix}=K\begin{bmatrix}
\frac{\mathrm{d}i_1}{\mathrm{d}t} \\
\frac{\mathrm{d}i_2}{\mathrm{d}t}
\end{bmatrix}
\]
\[\begin{bmatrix}
\dot{U_1}\\
\dot{U_2}
\end{bmatrix}=j \omega\begin{bmatrix}
L_1&\pm M \\
\pm M&L_2
\end{bmatrix}\begin{bmatrix}
\dot{I_1} \\\dot{I_2}
\end{bmatrix}=j \omega K\begin{bmatrix}
\dot{I_1} \\\dot{I_2}
\end{bmatrix}
\]
mutual reactance(互感电抗)
\[X_M=\omega M=2 \pi f M
\]
K:自己定义的常数矩阵
\[K=\begin{bmatrix}
L_1&\pm M \\
\pm M&L_2
\end{bmatrix}
\]
去耦等效
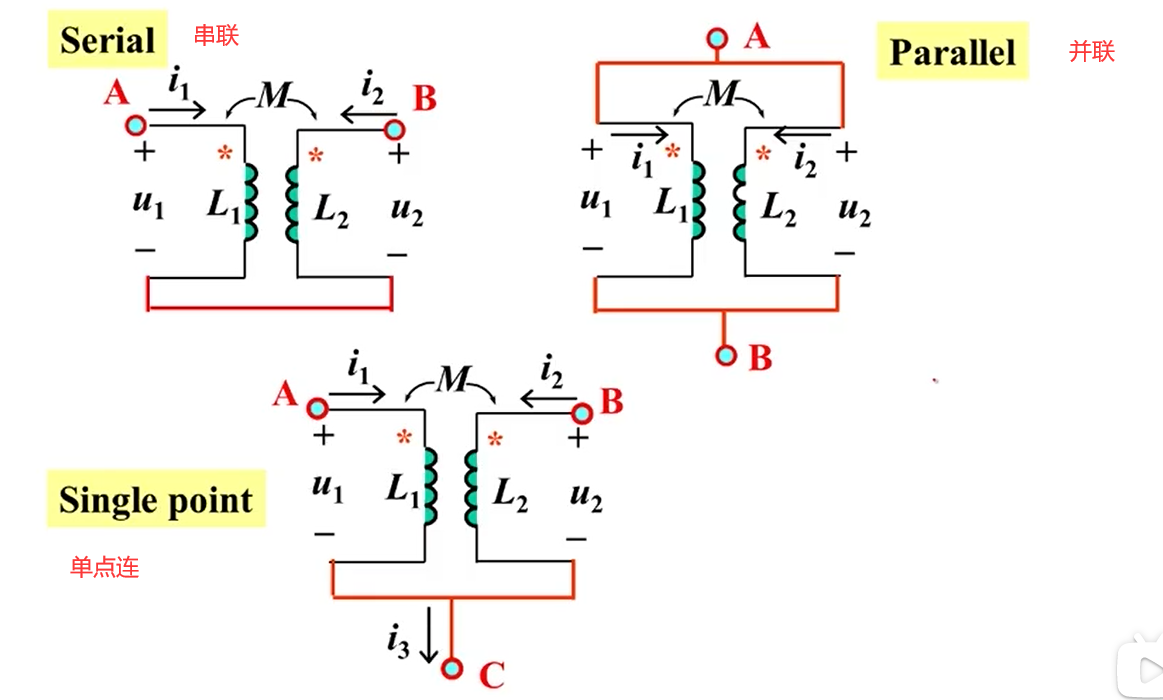
串联(Serial)
\[\begin{bmatrix}
\dot{U_1}\\\dot{U_2}
\end{bmatrix}= j\omega K\begin{bmatrix}
\dot{I} \\ \dot{I}
\end{bmatrix}
\]
\[Z=\frac{1}{\dot{I}}(\dot{U_1}+\dot{U_2})=j\omega \begin{bmatrix}
1&1
\end{bmatrix}K\begin{bmatrix}
1\\1
\end{bmatrix}=j \omega L_s
\]
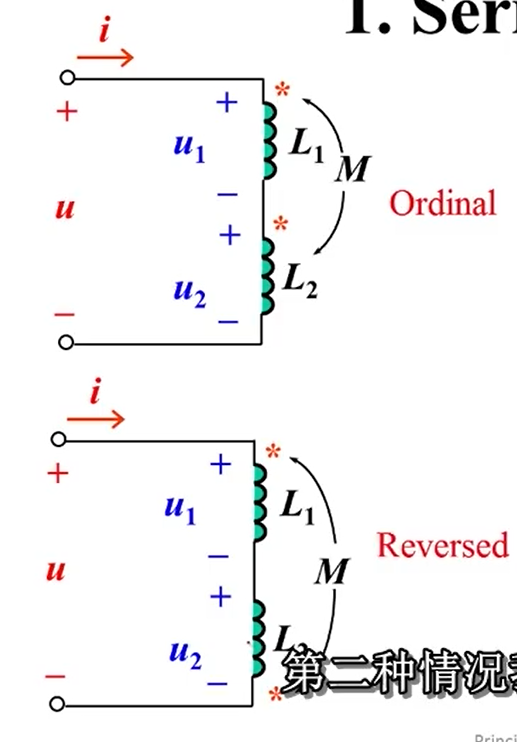
顺连
\[K=\begin{bmatrix}
L_1&M\\
M&L_2
\end{bmatrix}
\]
\[L_s=\begin{bmatrix}
1&1
\end{bmatrix}K\begin{bmatrix}
1\\1
\end{bmatrix}=L_1+L_2+2M
\]
逆连
\[K=\begin{bmatrix}
L_1&-M\\
-M&L_2
\end{bmatrix}
\]
\[L_s=\begin{bmatrix}
1&1
\end{bmatrix}K\begin{bmatrix}
1\\1
\end{bmatrix}=L_1+L_2-2M
\]
并联(Parallel)
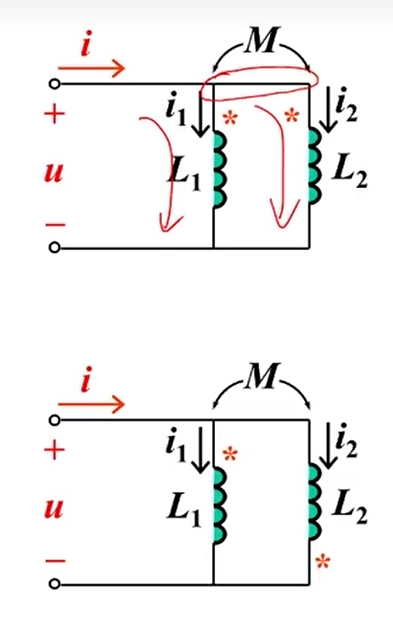
\[\begin{bmatrix}
\dot{U}\\\dot{U}
\end{bmatrix}=j\omega K\begin{bmatrix}
\dot{I_1}\\\dot{I_2}
\end{bmatrix}
\]
\[Y=\frac{1}{Z}=\frac{1}{\dot{U}}(\dot{I_1}+\dot{I_2})=j \omega
\begin{bmatrix}
1&1
\end{bmatrix}
K^{-1}
\begin{bmatrix}
1\\1
\end{bmatrix}=j \omega \frac{1}{L_p}
\]
顺连
\[K=\begin{bmatrix}
L_1&M\\
M&L_2
\end{bmatrix} \quad K^{-1}=\left[
\begin{array}{cc}
\frac{L_2}{L_1 L_2-M^2} & -\frac{M}{L_1 L_2-M^2} \\
-\frac{M}{L_1 L_2-M^2} & \frac{L_1}{L_1 L_2-M^2} \\
\end{array}
\right]
\]
\[\frac{1}{L_p}=\begin{bmatrix}
1&1
\end{bmatrix}K^{-1}\begin{bmatrix}
1\\1
\end{bmatrix}=\frac{L_1+L_2-2M}{L_1L_2-M^2}
\]
逆连
\[K=\begin{bmatrix}
L_1&-M\\
-M&L_2
\end{bmatrix} \quad K^{-1}\left[
\begin{array}{cc}
\frac{L_2}{L_1 L_2-M^2} & \frac{M}{L_1 L_2-M^2} \\
\frac{M}{L_1 L_2-M^2} & \frac{L_1}{L_1 L_2-M^2} \\
\end{array}
\right]
\]
\[\frac{1}{L_p}=\begin{bmatrix}
1&1
\end{bmatrix}K^{-1}\begin{bmatrix}
1\\1
\end{bmatrix}=\frac{L_1+L_2+2M}{L_1L_2-M^2}
\]
单点连(Single Point)
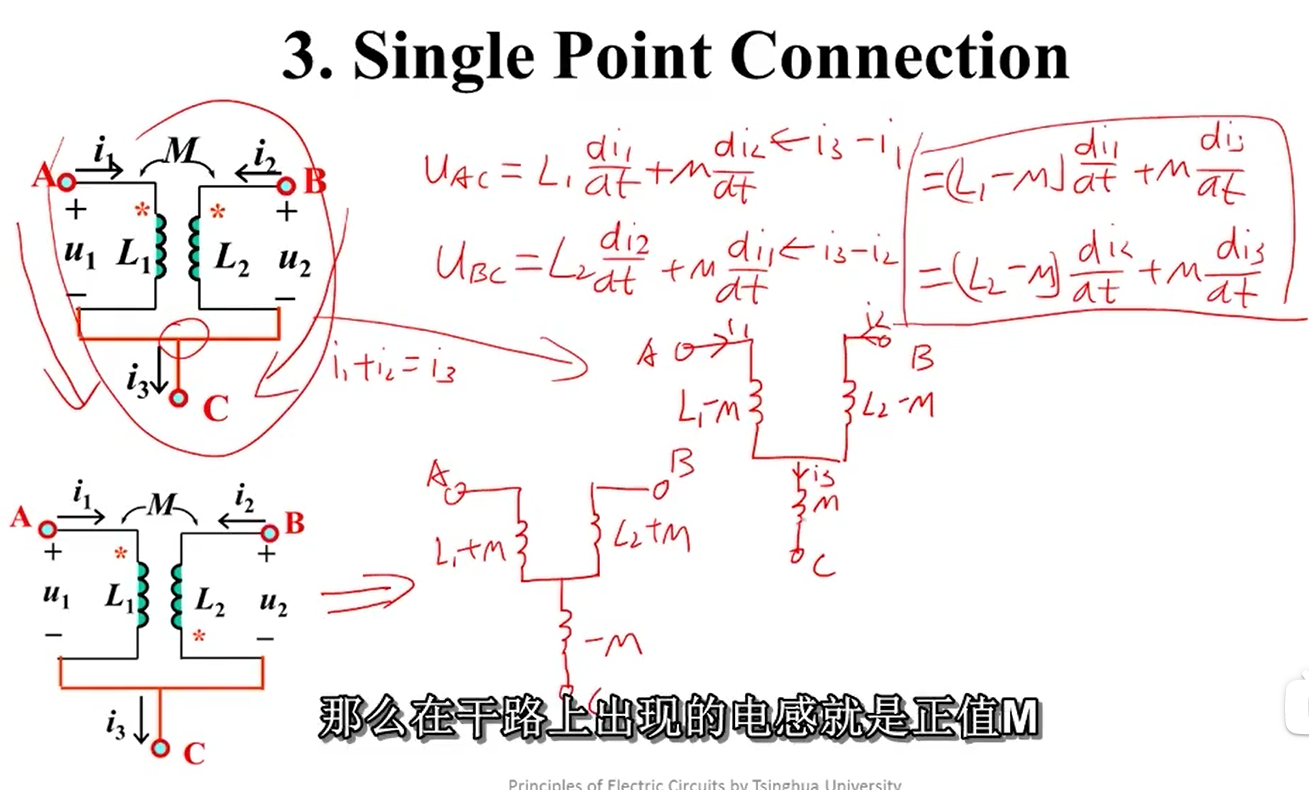
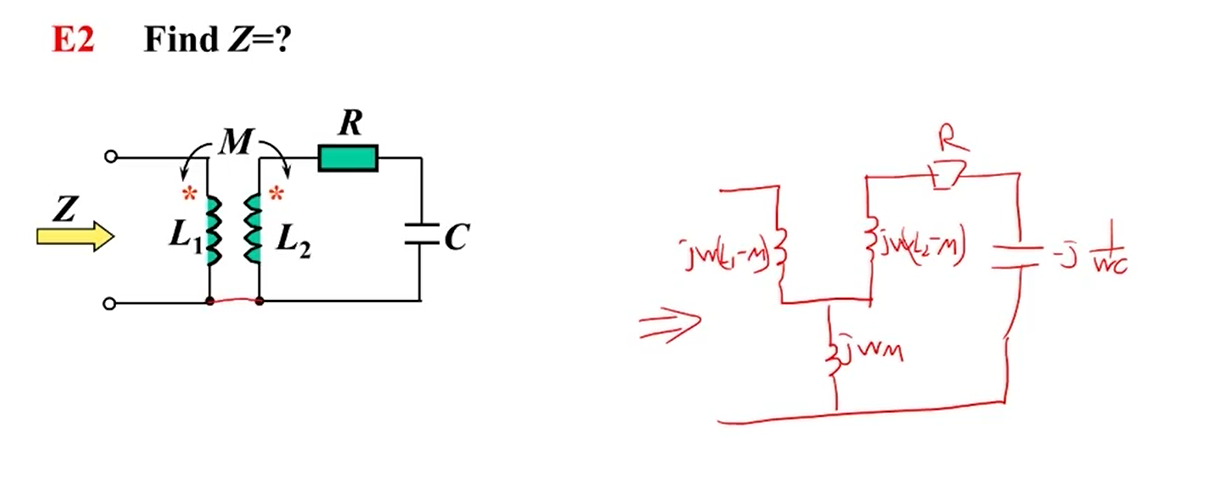
变压器(Transformer)
空芯变压器
我的评价是,直接解耦~~~~。
理想变压器
也直接解耦
变比
\[k_b=\frac{u_1}{u_2}=\frac{N_1}{N_2}
\]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号