正弦稳态分析
正弦量的定义和相量的引入
| 定义 | 说明 |
|---|---|
| 频率\(f\) | \(\displaystyle f=\frac{1}{T}\) |
| 角频率\(\omega\) | \(\omega=2\pi f\) |
| 初相位$\varphi $ | 同一频率下的正弦波的相位差始终是一个定值 |
| 振幅\(X_m\) | |
| 相量\(\dot{X}\) | \(\dot{X}=X_m \angle \theta=X_me^{\theta j} \hspace{0.3cm} \theta \in[-180,180]\) |
| 有效值\(X\) | \(\displaystyle X=\frac{\sqrt{2}}{2}X_m\) |
| 瞬时值\(x\) | \(x=x_m \cos \left( \omega t +\varphi \right)\) |
- \(X \in \{U,I\} \quad x\in \{u,i\}\)
超前,落后:看初始相位- 相量(Phase)只能反映一在正弦波的振幅和初相位,并且有关系
\[x=\mathrm{Im}\left[ e^{\omega tj}\cdot \dot{X} \right] \tag{1.1}
\]
并且我们可以很容易的写出正弦量\(x\)的微分积分关系(根据式(1.1))
\[\begin{align*}
\frac{\mathrm{d}{x}}{\mathrm{d}{t}}&=j \omega \mathrm{Im}\left[ e^{\omega tj}\cdot \dot{X} \right]=j \omega x \tag{1.2}\implies \frac{\mathrm{d}{\dot{X}}}{\mathrm{d}{t}}=j \omega \dot{X}\\
\int{x}\mathrm{d}t&=\frac{1}{ j \omega }\mathrm{Im}\left[ e^{\omega tj}\cdot \dot{X} \right]=\frac{x}{ j \omega }\implies \int{\dot{X}}\mathrm{d}t=\frac{\dot{X}}{j \omega} \tag{1.3}
\end{align*}
\]
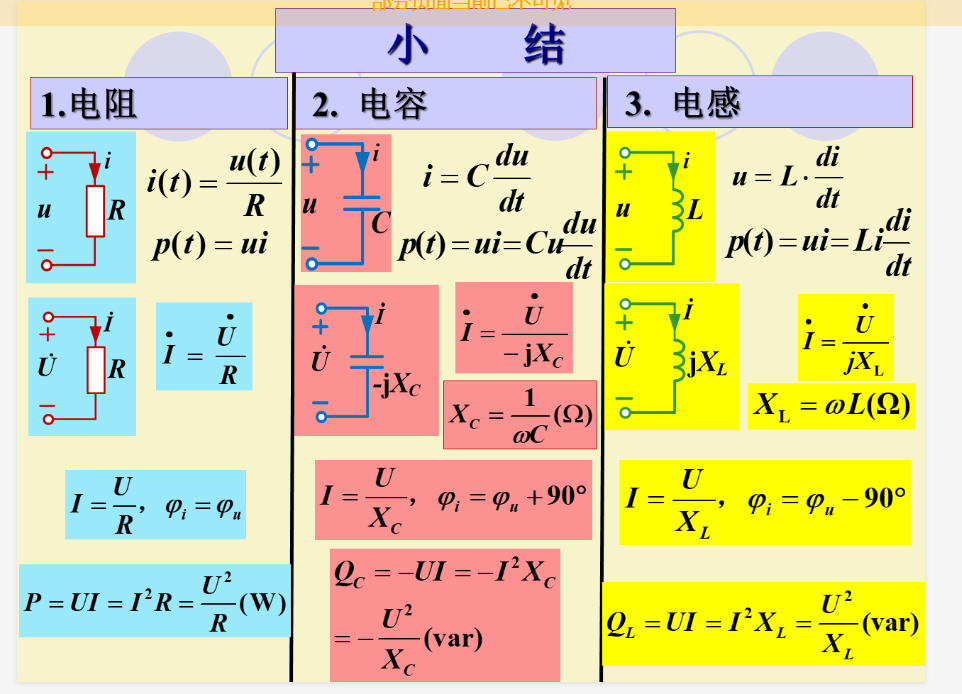
RLC 元件UI的相量关系
| 元件 | \(UI\)关系 | \(\dot{u}\dot{i}\)关系 | 说明 |
|---|---|---|---|
| 电阻 | \(u=Ri\) | \(\dot{U}=R\dot{I}\) | |
| 电容 | \(\displaystyle i=C\frac{\mathrm{d}{u}}{\mathrm{d}{t}}\) | \(\dot{I}=j\omega C\dot{U}\) | \(容抗\displaystyle X_C=\frac{1}{B_C(\text{容纳})}=\omega C\) |
| 电感 | \(\displaystyle u=L \frac{\mathrm{d}{i}}{\mathrm{d}{t}}\) | \(\dot{U}=j \omega L\dot{I}\) | 感抗\(X_L=\omega L\) |
- 实际情况往往复杂
复阻抗和复导纳
\[\begin{align*}
Z&=\frac{\dot{U}}{\dot{I}}=R+jX=ze^{j \varphi } \tag{3.1} \\
Y&=\frac{\dot{I}}{\dot{U}}=G+jB=ye^{j \varphi '} \tag{3.2}
\end{align*}
\]
其中一些定义如下表所示
| 名称 | 说明 | 名称 | 说明 |
|---|---|---|---|
| 电阻 | \(R=\mathrm{Re}[Z]\) | 电导 | \(G=\mathrm{Re}[Y]\) |
| 电抗 | \(X=\mathrm{Im}[Z]\) | 电纳 | \(G=\mathrm{Im}[Y]\) |
| 阻抗角 | \(\displaystyle \varphi=\arctan \frac{X}{R}=\varphi_u-\varphi_i\) | 阻纳角 | \(\displaystyle \varphi'=\arctan \frac{B}{G}=\varphi_i-\varphi_u\) |
| 模 | ~ | ~ | ~ |
相量图
- (1)同频正弦量才能表示在同一个相量图中;
- (2)选定一个参考相量(设初相位为零)。
功率
对于一二端元件,我们假设其电流为\(i=I_m \cos \left(\omega t\right)\),电压\(u=U_m \cos \left( \omega t+\varphi \right)\)。并且一些常用概念如下表
| 概念 | 阐述 | 说明 |
|---|---|---|
| 功率因数 | \(\cos \left( \varphi \right)\) | 越大说明阻性成分越高 |
| 向量图 | 一系列正弦波的向量\(在t=0\)时候的位置 | |
| 平均功率/有效功率/额定功率 | \(UI \cos \left( \cos \right)\) |
瞬时功率
\[p=ui=U_mI_m\cos (\omega t)\cos \left( \omega t+\varphi \right)
\]
平均功率(有功功率,额定功率)
\[P=ui\cos \varphi
\]
无功功率
\[Q=UI \sin \varphi
\]
视在功率
\[S=UI=\sqrt{Q^2+S^2}
\]
功率因数
\[F_p=\cos \varphi=\frac{p}{EI}=\frac{I^2R}{EI}=\frac{R}{|Z_T|}=\frac{P}{S} \tag{4.4}
\]
- 感性无功和容性无功
最大功率传输定理
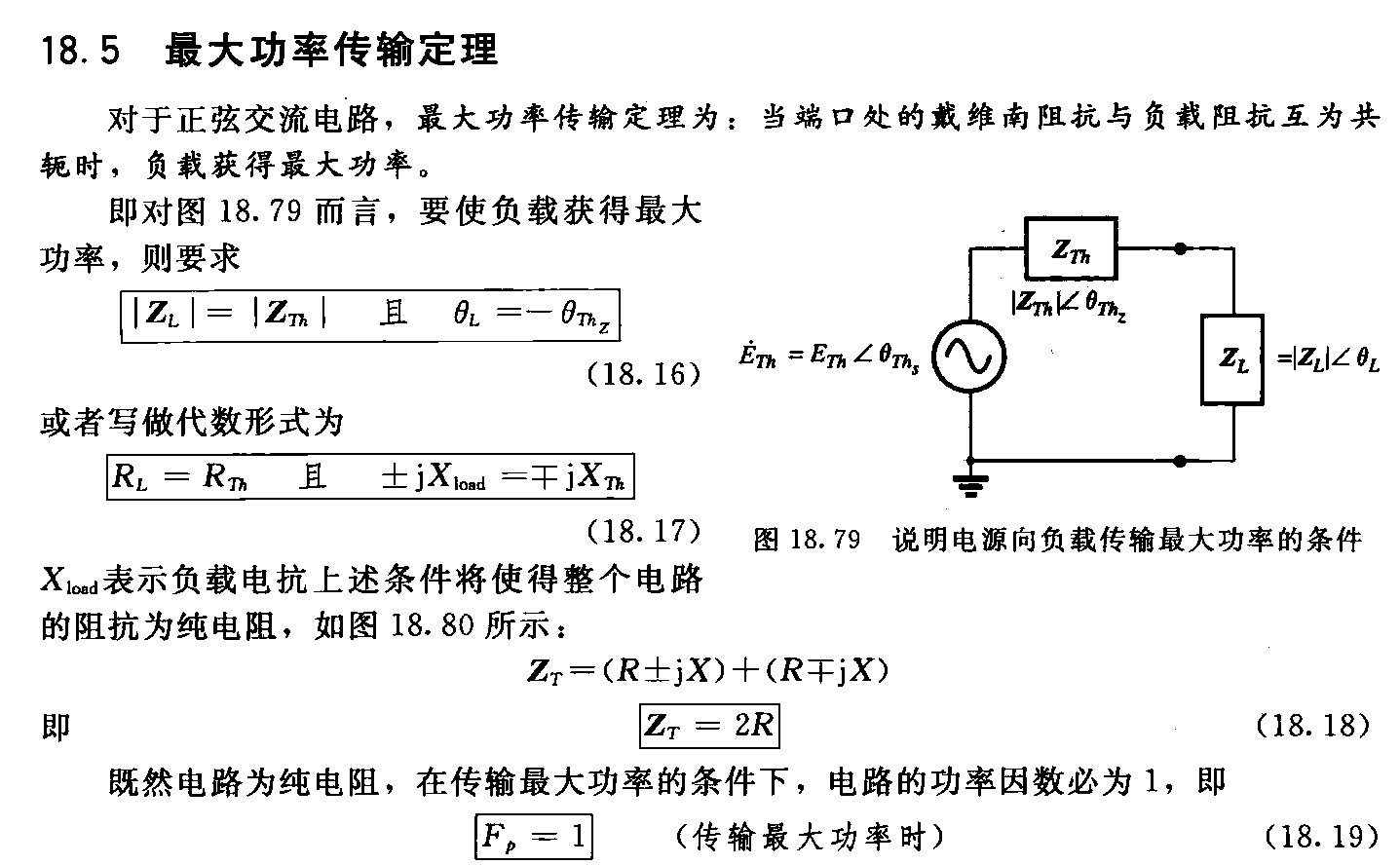
模匹配
TODO: ADD THIS
复功率
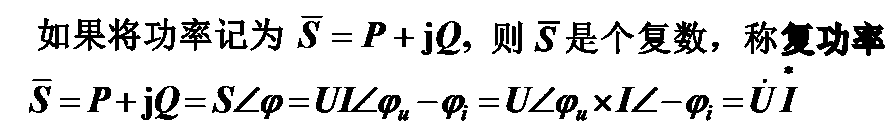
具体例子
| 类型 | 瞬时功率 | 平均功率 | 无功功率 |
|---|---|---|---|
| 电阻 |