二端网络
概览
本章主要研究在内部受限的情况下,如何进行二端口的端口分析,将建立二端口网络的三种参数:阻抗(z)参数、导纳(y)参数和混合(h)参数。本章末尾的表26.1将讨论这三种参数的转换关系。(
抽象,等效,分析方法))
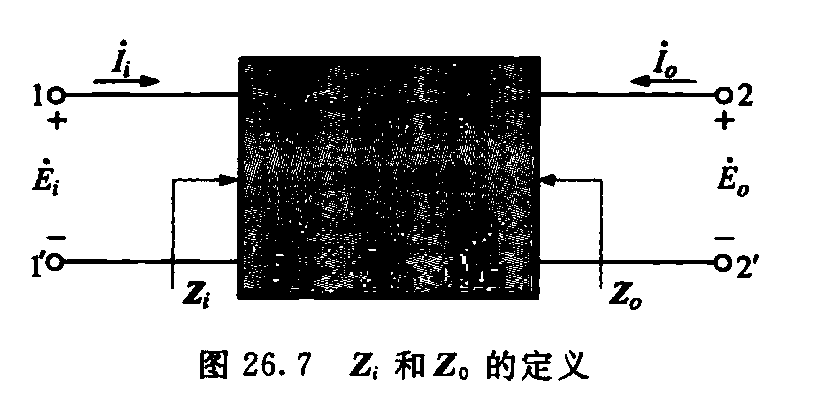
- 区分二端网络,二端口网络
- 本章只讨论
不含独立源的线性双端电路
定义
| 名称 | 定义 | 说明 |
|---|---|---|
端口(Port) |
两个接线端,满足一个接线端流入的电流等于另外一个接线端流出的电流 | |
二端口(Two-Port) |
一个电路和外接通过两个端口链接的时候就叫做二端口 | |
互易二端口 |
参数矩阵\(A=A^T\) | |
对称二端口 |
参数矩阵\(A_{11}=A_{22} \quad and \quad A=A^T\) | |
(短路)导纳参数方程Y |
\(\left[ \begin{array} { l } { i _ { 1 } } \\ { i _ { 2 } } \end{array} \right] = \left[ \begin{array} { l } { G _ { 11 } } & { G _ { 12 } } \\ { G _ { 21 } } & { G _ { 22 } } \end{array} \right] \left[ \begin{array} { l } { u _ { 1 } } \\ { u _ { 22 } } \end{array} \right]\) | \(G_{ij}=\frac{\dot{I}_j}{\dot{U}_j}|_{U_i=0}\) |
(开路)阻抗参数方程Z |
\(\left[ \begin{array} { l } { u _ { 1 } } \\ { u _ { 2 } } \end{array} \right] = \left[ \begin{array} { l } { R _ { 11 } } & { R _ { 12 } } \\ { R _ { 21 } } & { R _ { 22 } } \end{array} \right] \left[ \begin{array} { l } { i _ { 1 } } \\ { i _ { 2 } } \end{array} \right]\) | \(R_{ij}=\frac{\dot{U}_j}{\dot{I}_j}|_{I_i=0}\) |
(短路)导纳参数方程和阻抗参数方程
求解
- 列写电路定理,KVL,LCL。
- 导纳参数方程一侧加
电压源,一侧短路 - 阻抗参数方程一侧加
电流源,一侧开路 - 同时对于所有的纯电阻二端网络,我们可以知道其都是
互易二端口

