2023-02-25 22:11阅读: 150评论: 0推荐: 0

储能元件和暂态分析

储能元件

电容(Capacitors)

$\begin{tikzpicture}[] \node[] (A) at (0,0) {}; \node[] (B) at (4,0) {}; \node (a) at (1,1) {}; \node (b) at (3,1) {}; \node (c) at (1,-1) {}; \node (d) at (3,-1) {}; \node at (0.7,0.5) {$+Q$}; \node at (3.3,0.5) {$-Q$}; \node at (0.7,-0.5) {$S$}; \node at (3.3,-0.5) {$S$}; \draw[semithick] (a) to (c); \draw[semithick] (b) to (d); \draw (A) to (1,0); \draw (B) to (3,0); \draw[] (A) circle (0.10) (B) circle (0.1); \draw[-latex] (1,-0.5) to (3,-0.5); \draw[-latex] (3,-0.5) to (1,-0.5); \node[below] at (2,-0.4) {$d$}; % \fill[pattern={Lines[angle=45,yshift=-.5pt,distance=3pt]}](1,1) rectangle (3,-1); \end{tikzpicture}$

\begin{matrix} (1.1.1) & ∮ \vec{D} \cdot \vec{d S} = D Δ S = \frac{Q}{S} Δ S \end{matrix}

$\oint{\vec{D}\cdot \vec{\mathrm{d}{S}}}=D \Delta S=\frac{Q}{S}\Delta S \tag{1.1.1}$

假设是线性均匀场，所以可以得到

\begin{matrix} (1.1.2) & E = \frac{S}{ϵ} = \frac{Q}{ϵ S} ⟹ U = \int_{A}^{B} E d l = \frac{Q D}{ϵ S} \end{matrix}

$E=\frac{S}{\epsilon}=\frac{Q}{\epsilon S}\implies U=\int_{A}^B{E\mathrm{d}{l}}=\frac{QD}{\epsilon S} \tag{1.1.2}$

定义不变量电容 $C$

\begin{matrix} (1.1.3) & C = \frac{Q}{U} = \frac{ϵ d}{d} (F) \end{matrix}

$C=\frac{Q}{U}=\frac{\epsilon d}{d} \hspace{0.2cm} (\mathrm{F}) \tag{1.1.3}$

给出电压电流的表达形式（关联参考方向下）

\begin{aligned} (1.1.4) & i & = \frac{d Q}{d t} = C \frac{d u}{d t} \\ (1.1.5) & U & = \frac{1}{C} \int_{- \infty}^{+ \infty} i d t = U (0) + \frac{1}{C} \int_{0}^{+ \infty} i d t \end{aligned}

$\begin{align} i&=\frac{\mathrm{d}{Q}}{\mathrm{d}{t}}=C \frac{\mathrm{d}{u}}{\mathrm{d}{t}} \tag{1.1.4} \\ U&=\frac{1}{C}\int_{-\infty}^{+\infty}i\mathrm{d}{t}=U(0)+ \frac{1}{C}\int_{0}^{+\infty}i\mathrm{d}{t} \tag{1.1.5} \end{align}$

接下来我们在关联参考方向上考虑其能量[假设 $u(-\infty)\thickapprox 0$ ]：

\begin{aligned} (1.1.6) & P & = \pm u i = (\pm u) \cdot [\pm C \frac{d u}{d t}] \\ (1.1.7) & W (t) & = \int_{- \infty}^{t} P d t = C \int_{- \infty}^{t} u d u = \frac{1}{2} C u^{2} (t) = \frac{Q^{2} (t)}{2 C} \end{aligned}

$\begin{align*} P&=\pm ui=(\pm u) \cdot \left[\pm C \frac{\mathrm{d}{u}}{dt} \right] \tag{1.1.6} \\ W(t)&=\int_{-\infty}^{t}{P\mathrm{d}{t}}=C\int_{-\infty}^{t}{u\mathrm{d}{u}}=\frac{1}{2}Cu^2(t)=\frac{Q^2(t)}{2C} \tag{1.1.7} \\ \end{align*}$

直流的话 $i=0$ ，相当于开路。
记忆元件，储能元件， $t$ 时刻存储的能量仅与 $u(t)$ 有关。
电流 $i$ 与参考方向有关，但是 功率没有。

对于电流关联为正，非关联为负

这和我们对电容 $C$ 的定义和对电动势方向的理解有关系，在我们的推导过程中，场强的方向（电势下降的方向）和电荷转移的方向是一致的，所以参考方向的话，我们得到的电流会是正值。

电容的串并联

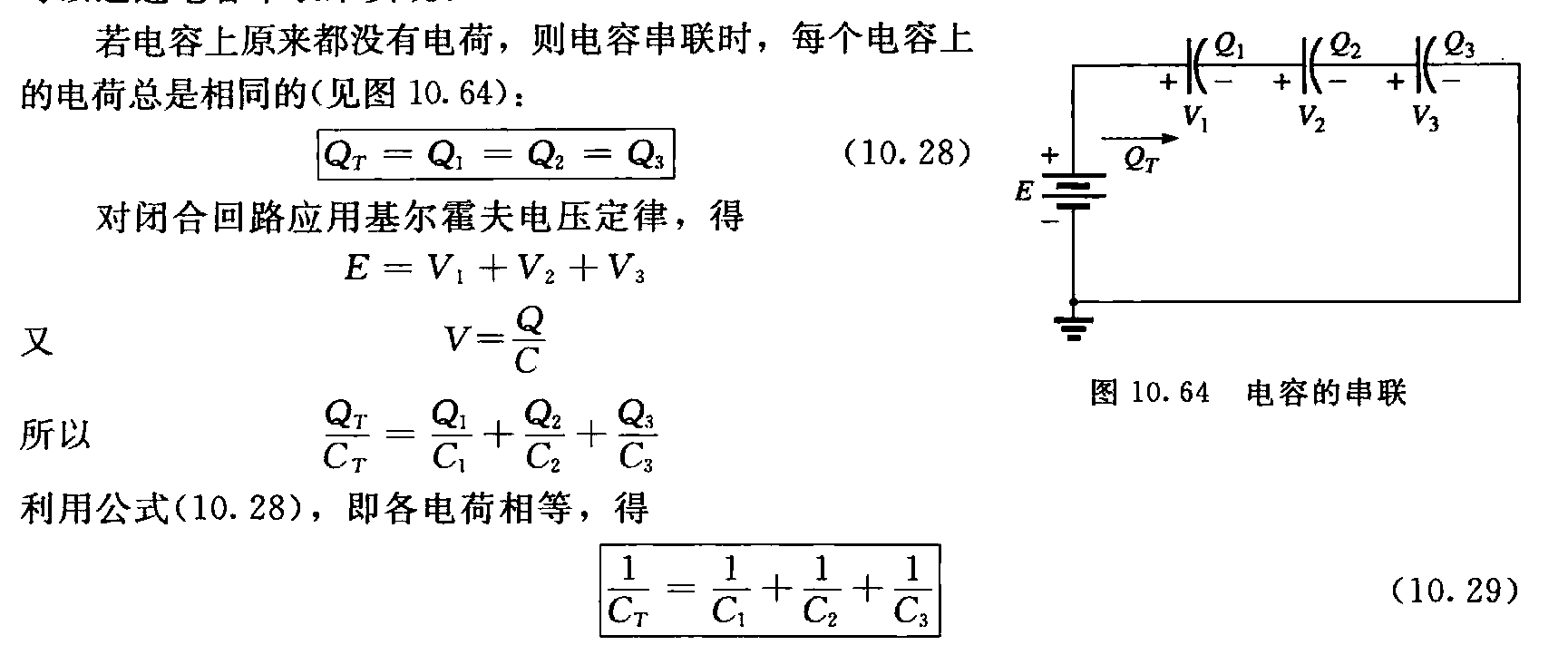
串联通过他们的电流相等,所以 $Q(t)=\int_{0}^{t}{i}\mathrm{d}t$ 相同。
并联的话， $i_T=\sum_{n}i_j\implies Q_T=\sum_{n}Q_j$

电感

电感同样是储能元件，只不过跟电容存储电场能量不一样，它存储的是磁场的能量。
在带有磁心或是不带磁心的线圈中通以电流，会在线圈内部和周围形成磁场。这种元件（见图11.16）被称做电感器。

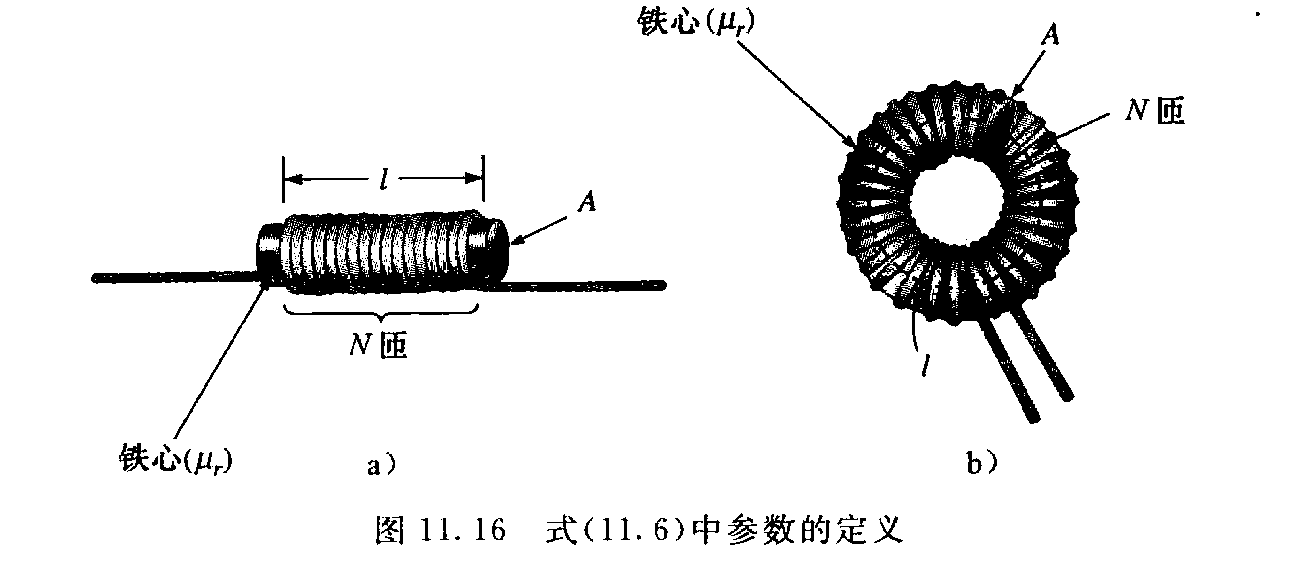
并且我们可以知道电感的值为

L = \frac{μ N^{2} A}{l} = μ_{r} L_{0}

$L=\frac{\mu N^{2} A}{l}=\mu_rL_0$

式中, $\mu$ 是磁导率, 单位为 $\mathrm{Wb} / \mathrm{A} \cdot \mathrm{m}$ ; N 是线圈匝数; A 是磁心的横截面积, 单位为 $\mathrm{m}^{2}$ ; $l$ 是线圈长度, 单位为 $\mathrm{m}$ ; $L$ 是电感值, 单位为 $\mathrm{H}$ 。

下面我们求解其感生电压：

e = N \frac{d Φ}{d t} = N \frac{d Φ}{d i} \frac{d i}{d t} = L \frac{d i}{d t}

$e=N \frac{\mathrm{d}{ \Phi}}{\mathrm{d}{t}}=N \frac{\mathrm{d}{\Phi}}{\mathrm{d}{i}} \frac{\mathrm{d}{i}}{\mathrm{d}{t}}=L \frac{\mathrm{d}{i}}{\mathrm{d}{t}}$

其和电流感应电流公式类似，其他参数结果也类似，请自行推导，略去证明。

电感的串并联

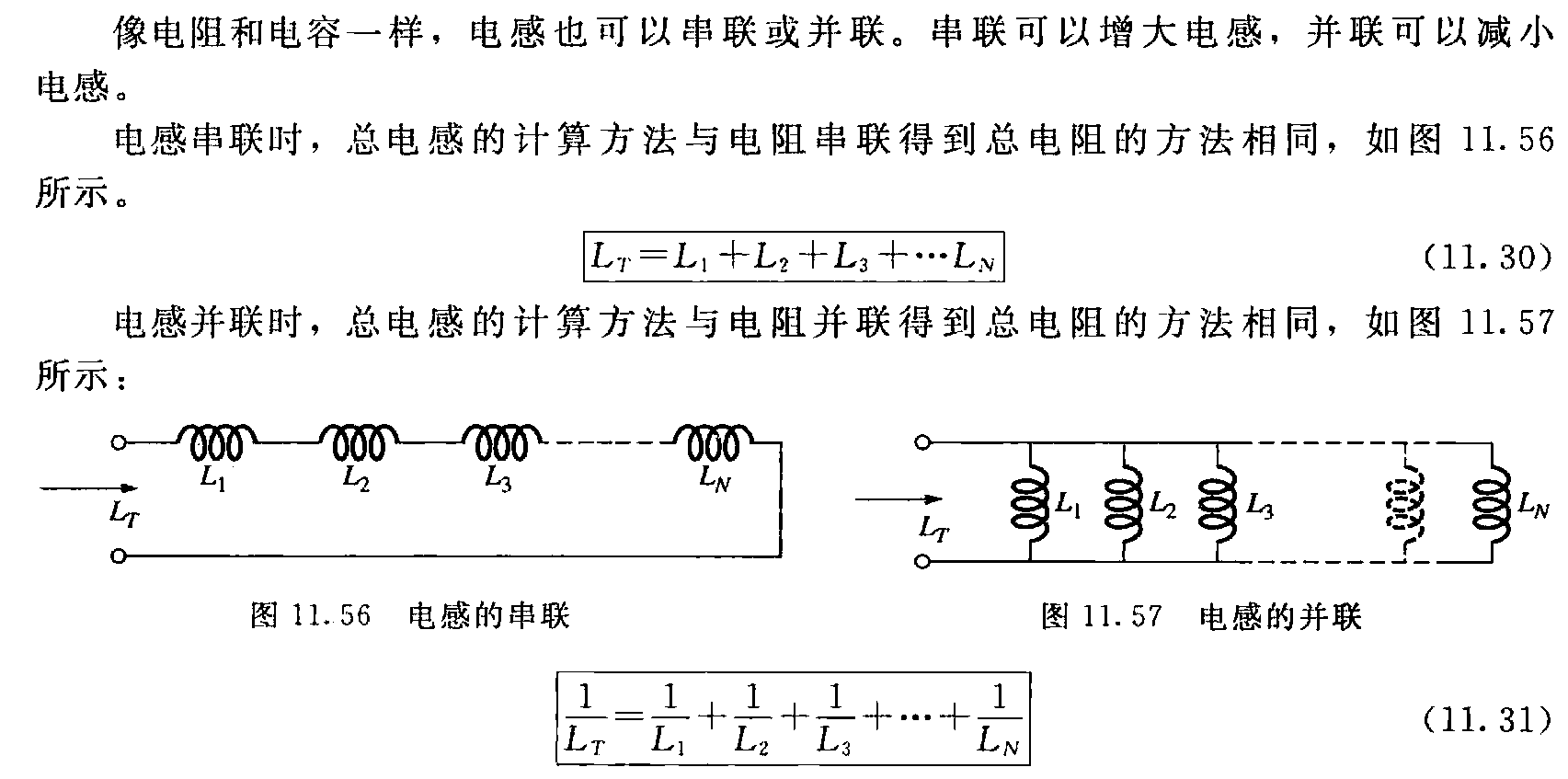
展开/收起证明过程

其实方法和上面是类似的，对于串联: $\displaystyle \frac{\mathrm{d}{i_j}}{\mathrm{d}{t}}$ 都相等，所以有

L_{总} = \frac{\sum v_{j}}{\frac{d i_{j}}{d t}} = \sum [L_{j}]

$L_{总}=\frac{\sum{v_j}}{\frac{\mathrm{d}{i_j}}{\mathrm{d}{t}}}=\sum\left[ L_j \right]$

对于并联,电压都相等：

\frac{1}{L_{总}} = \frac{\sum \frac{d i_{j}}{d t}}{v} = \sum \frac{1}{L_{j}}

$\frac{1}{L_{总}}=\frac{\sum{\frac{\mathrm{d}{i_j}}{\mathrm{d}{t}}}}{v} =\sum{\frac{1}{L_j}}$

附录

$m$	$\mu$	$n$	$p$
$10^{-3}$	$10^{-6}$	$10^{-9}$	$10^{-12}$

单位表

单位	说明1	说明2
库伦 $\hspace{0.2cm} \mathrm{C}$	电荷量 $Q$ 的单位	$1C=6.242 \times 10^{18}\text{电子}$
法拉利 $\hspace{0.2cm} \mathrm{F}$	电容 $C$ 的单位
特斯拉 $\hspace{0.2cm} \mathrm{T}$	磁感应强度B的单位	$1 \mathrm{T}=1 \mathrm{Wb}$
韦伯 $\hspace{0.2cm} \mathrm{Wb}$	磁通量的单位