电路定理
本章介绍一些童要的电路定理,包括叠加定理(舍齐性定理),替代定理,戴维南定理,诺顿定理,最大功率传输定理,特勒根定理、互易定理,并扼要介绍有关对偶原理的概念。
预览
| 电路定律 | 定理简单说明 | 适用范围 |
|---|---|---|
| 叠加定理 | 激励源单独作用线性组合 | 线性电路[1] |
| 齐性原理(homogeneity propert) | 响应和激励成正比 | 一个独立源(可以推广到线性电路[1:1]) |
| 替代定理 | 一端口网络可被替代成激励源 | 任意一端口网络(条件见下边)) |
| 戴维南定理 | 等效成理想电压源和电阻串联 | 存在独立源和电阻、受控源的线性网络 |
| 诺顿定理 | 等效成理想电流源和电阻并联 | 同上 |
| 其他方法 | 1.电源转移 |
叠加定理
叠加定理可表述为:
在线性电阻电路中,某处电压或电流都是电路中各个独立电源单独作用时,在该处分别产生的电压或电流的叠加。
- 仅仅适用于线性电路[1:2],功率不能用
- 独立作用:不作用的电压源开路,电压源处用短路代替
展开/收起证明过程
由节点电压法或者回路电流法列写出一个有着\(b\)个支路和\(k\)个节点的电路的方程组形式:
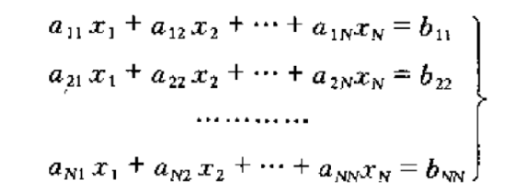
我们可以显然地知道右端\(b_{kk}\)是激励源的叠加作用效果;(对于两种源混合,并且含有独立源的来说,见下)
如果使用回路电流法中遇到了无伴电流源\(I_S\),其电阻无限大,列写困难,我们可以引入\(U_S\) 的概念,将原n个方程组列写成\(n-1\) 个方程组,右边多了\(I_S\)的激励,以此类推,不再赘述。
求解方程组的解,我们使用克莱姆法则[2]将其求出,此时每个\(x_i\)都是多个激励源的线性叠加形式,而我们要求解的电压电流是多个\(x_i\)的线性叠加,类似以下形式
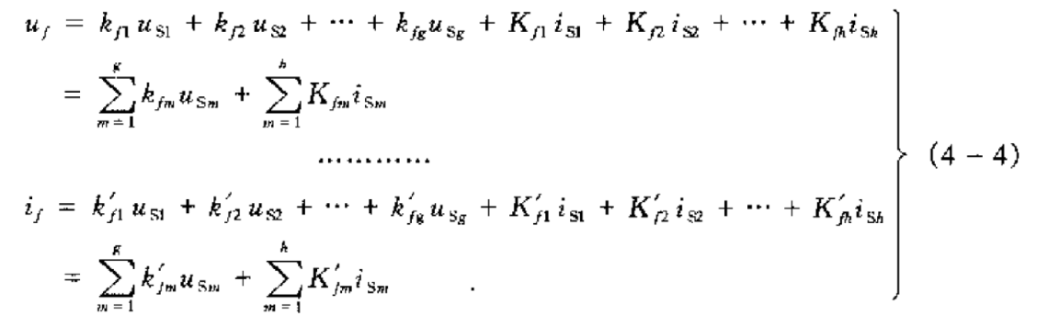
那显然我们只考虑一个激励源对其影响的时候其他源就要置为0
一个含有受控源的叠加定理的说明
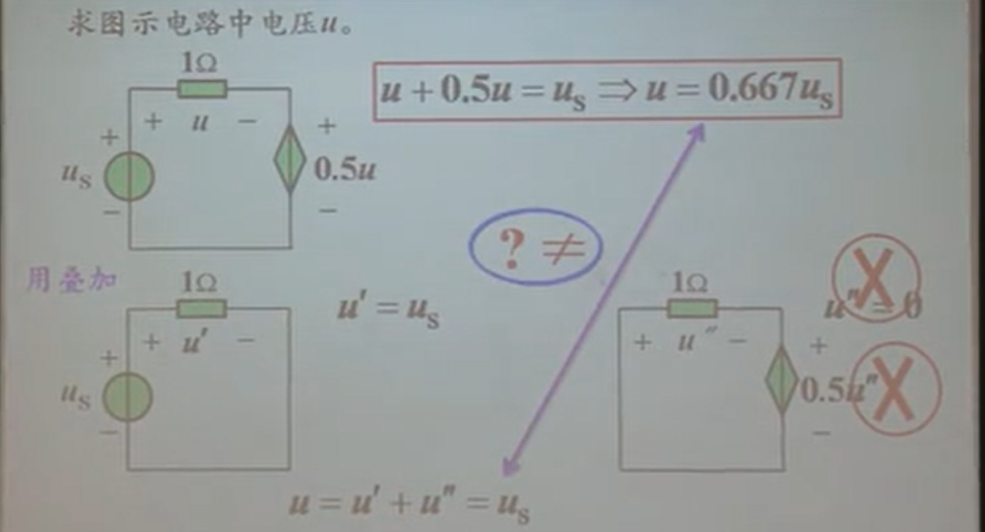
通过一些处理,在运用叠加定理时可以将受控源像独立源一样让其单独作用,从而对电路进行求解。但需要强调的是,这仅仅是一种解题技巧,不是叠加定理的本质;并且这样处理的结果往往会由于概念不清导致结果错误。
这里其实就是写错了受控激励源的控制量而已,so easy。
齐性原理(homogeneity propert)
当电路中只有一个激励(独立源)时,则响应(电压或电流)与激励成正比。显然这个定义也可以推广到线性电路[1:3] ,用齐性定理分析梯形电路[3]特别有效。
下面我们来看个例子,求下图各支路电流
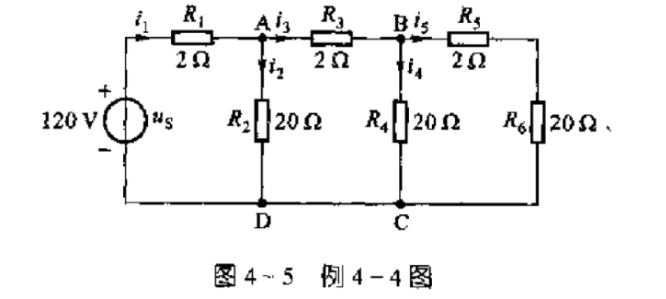
我们先假设\(i_5=i_5'=1A\),然后根据一系列关系倒推导出\(U_S=30.02\hspace{0.1cm} \mathrm{V}\)

这种方法叫做“倒推法”。
替代定理
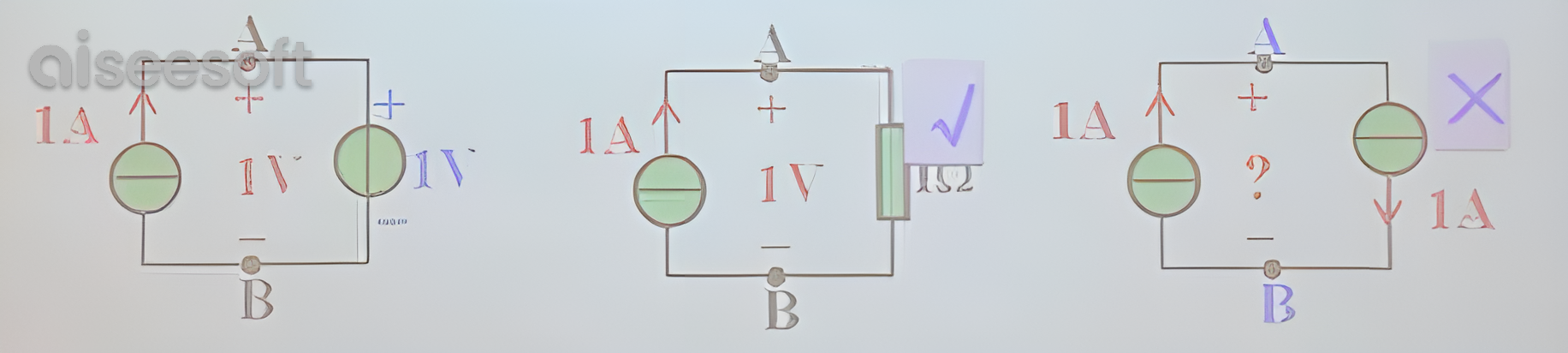
替代定理不仅适用于线性电路, 也适用于非线性电路。
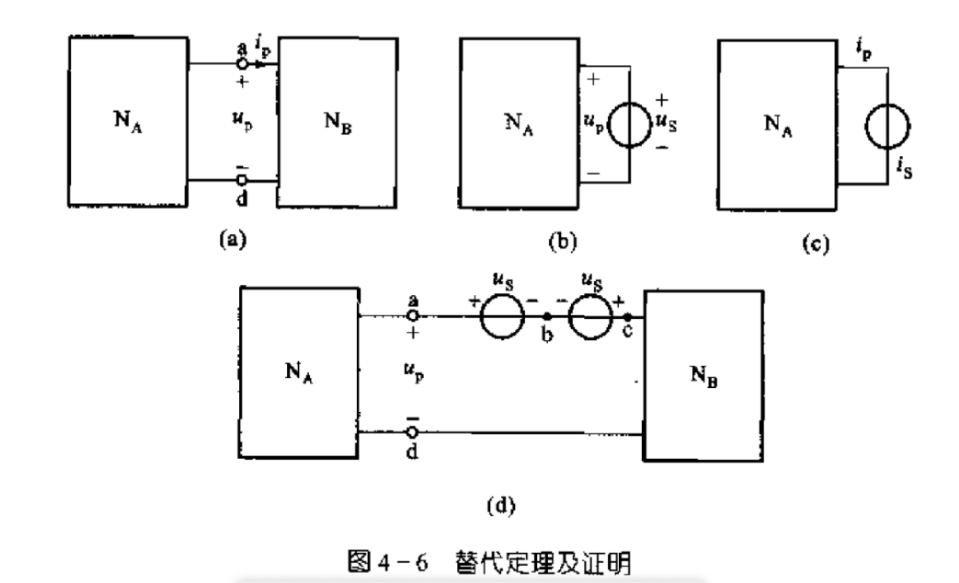
已知\(N_{A}\)与 \(N_{B}\)两个一端口网络端口电压 \(u_{\mathrm{p}}\)与电流 \(i_{\mathrm{p}}\), 用一\(u_{\mathrm{S}}=u_{\mathrm{p}}\)[4] 电压源或一\(i_{\mathrm{S}}=i_{\mathrm{p}}\)电流源替代其中任一网络, 而另一个网络的内部压流维持不变。
图 4-6(a) 是原电路, 图 4-6(b) 是将\(\mathrm{N}_{\mathrm{B}}\)替代为一个电压源\(u_{5}\); 图 4-6(c) 是将\(\mathrm{N}_{\mathrm{B}}\)热代为一个电流源\(i_{\mathrm{S}}\)。
展开/收起证明过程
如图 4-6(c)所示,另外一个证明方法,其实也同理。- 替代后具有唯一解
-
- 没有耦合关系(非要用,等效替代)
戴维南定理
对于一个没有独立电源的电路,其端口电压和电流成比例关系,可以等效成一个电阻。
注意在求解这种电路的等效电阻时候,应外接激励。同时非参考方向出来的才是正电阻。
为什么可以这么说?
我们可以先将其内部的受控源当作独立源,列写回路电流或节点电压方程,我们得到的方程组右边定只有外部激励或内部受控源的激励。
但是内部的受控源的激励一定可以写成左边变量\(I_{ii}/U_{ii}\)又或者外部激励的组合。也就是说方程组右边将有且仅有外部激励项。
所以,证毕。
为什么是非参考方向?
那么,对于内部存在着独立源的电路,我们又应该去怎么等效呢?我们接下来给出戴维南定理:
任何一个含有独立电源、线性电阻和线性受控源的一端口网络,可以用一个独立电压源\(u_s\)和电阻\(R\)的串联组合来等效替代,其中电压等于端口开路电压,电阻\(R\)等于端口中所有独立电源置零后端口的入端等效电阻。
展开/收起证明过程
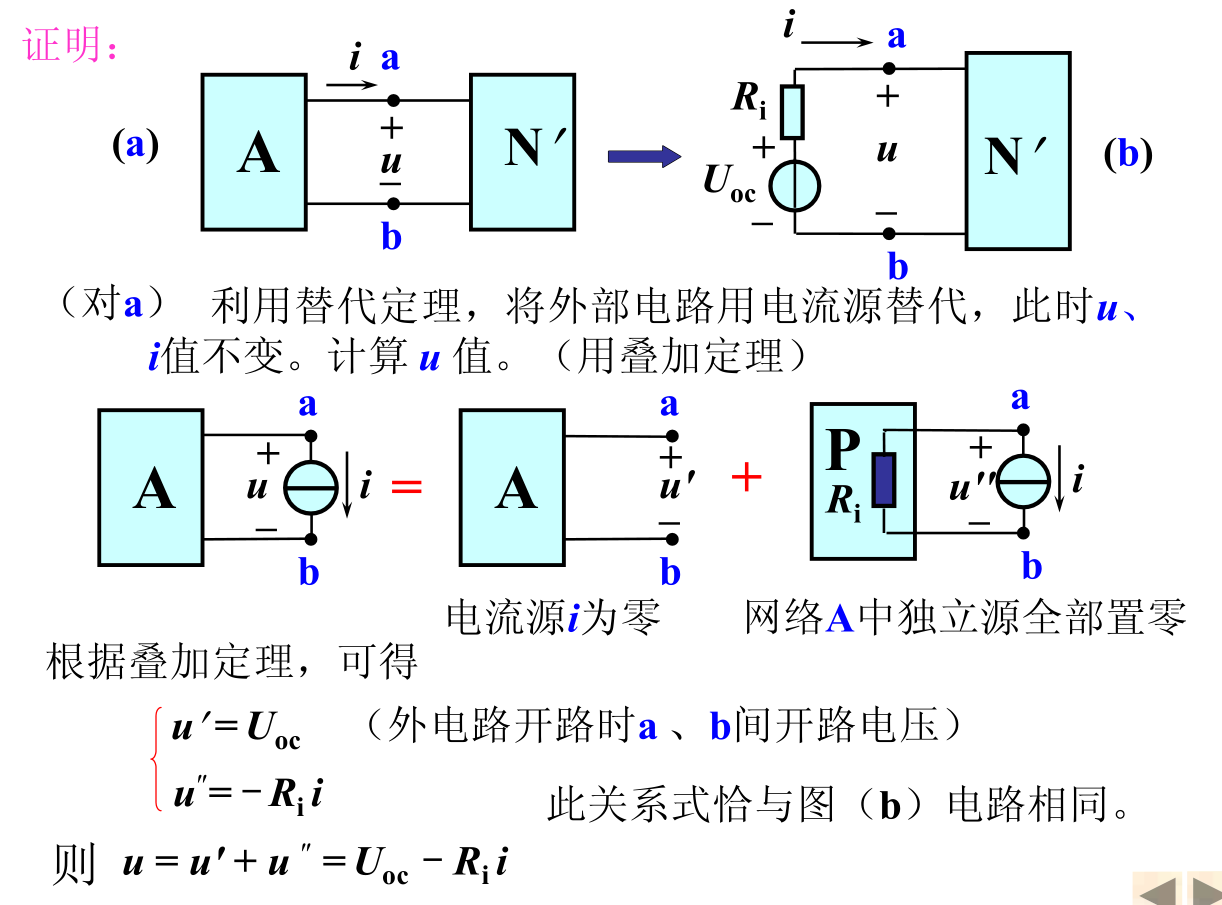
如何求解这个入端等效电阻
- a. 网络内部不含有受控源时可采用电阻串并联的方法计算。
- b. 端口加电压求电流法或加电流求电压法(
内部独立源置零)。 - c. 等效电阻等于端口的开路电压与短路电流的比 (内部独立源保留) 。
- 当一端口内部含有受控源时,控制支路与受控源支路必须包含在被等效变换的同一部分电路中。
- 注意
参考方向,如果内部有受控源的的话,可能是负电阻。
Some Example
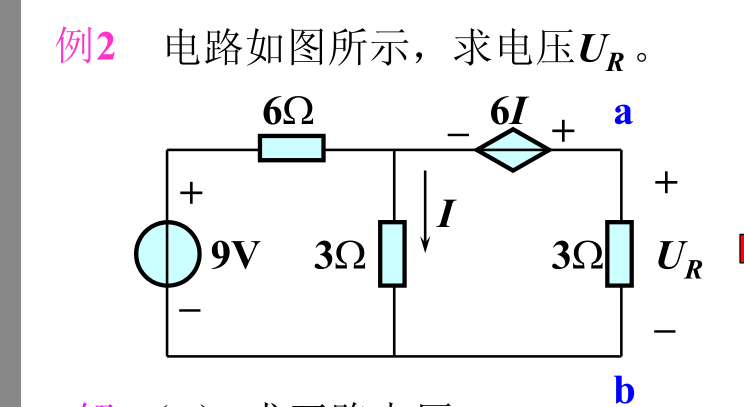
例题
- 求出开路电压\(U_S=9V\),求出等效内阻\(R=6\Omega\),\(U_R=3V\)
放大器的例子
TODO:ADD THIS
诺顿定理
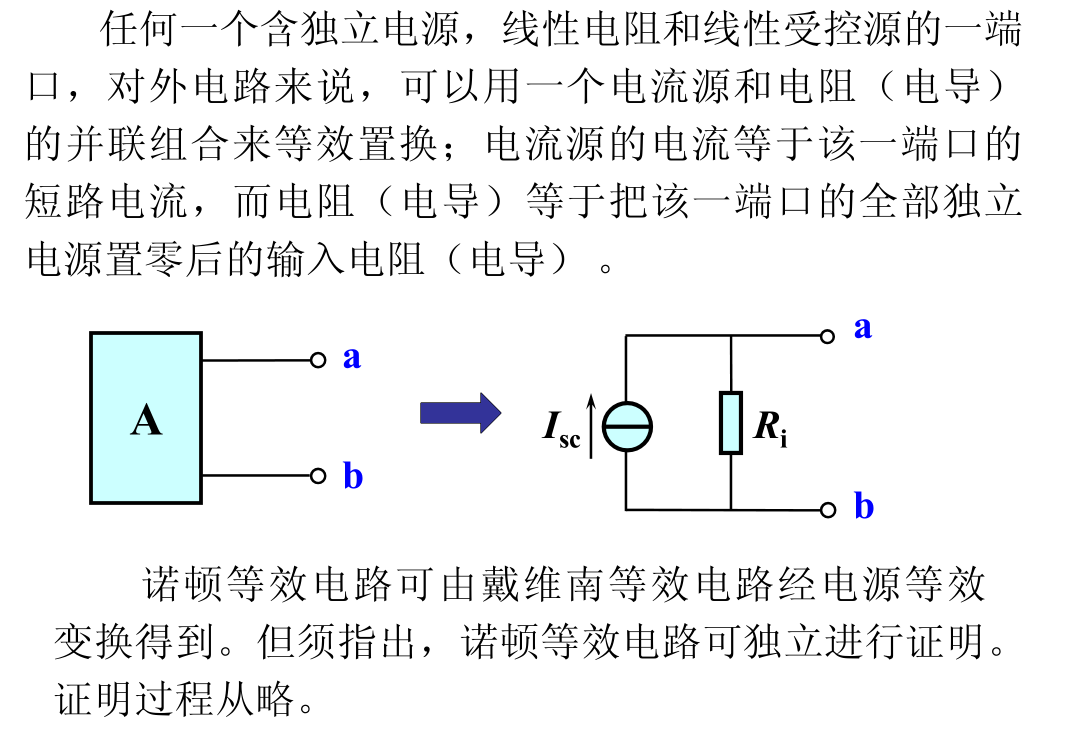
其他方法
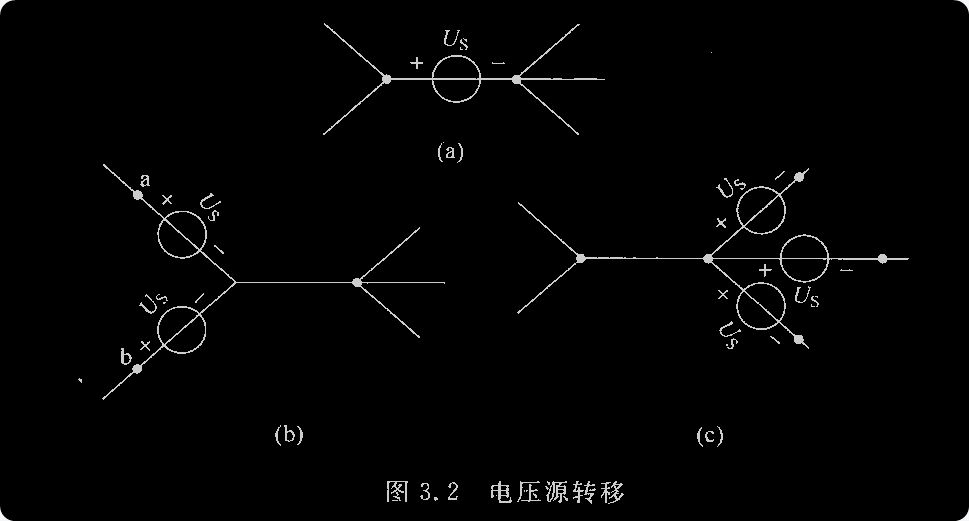
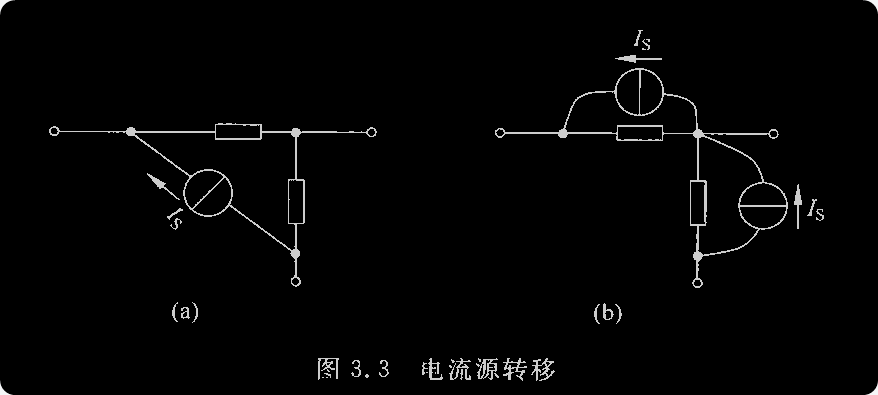
电源转移
应用节点法分析电路时,有时会遇到两个独立节点之间接有单独一个理想电压源的情况。下面介绍一种可以有效解决这种问题的一个方法:电源转移。
所谓源转移,本质上就是在满足基尔霍夫定律的前提下,改变电源的位置,得到原电路的一个等效电路。
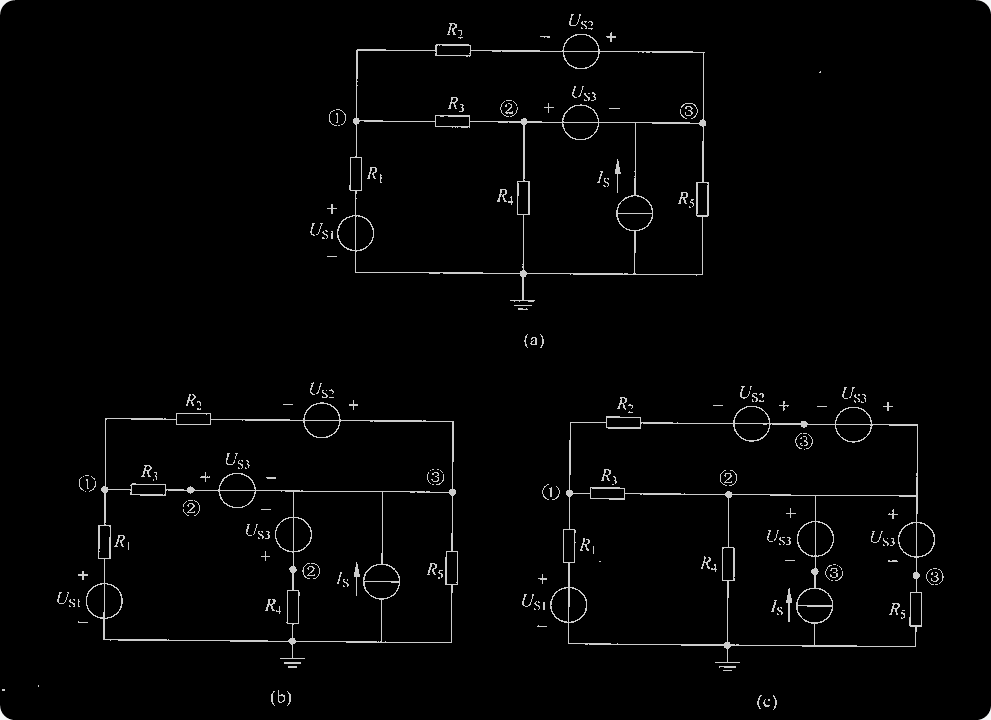
A Example
附录
参考内容
- 《电路》邱关源-第五版
- BASIC CIRCUIT CONCEPTS[一个牛人的电路博客]
- 于歆杰 《电路原理导学导教》
- 王竹萍.受控源当作独立源处理的叠加定理分析方法[J].电气电子教学学报,2005(03):26-27+32.全文阅读--XML全文阅读--中国知网 (cnki.net)
引用和注解
线性电路是指完全由线性元件、独立源或线性受控源构成的电路[1]。这些线性元件的电阻R,电流I,电压U之间的联系有欧姆定律:U=R*I,这表明它们之间的联系是线性联系[2],而不是曲线联系。 ↩︎ ↩︎ ↩︎ ↩︎
- 克莱姆法则,又称克拉默法则(Cramer's Rule),是线性代数中一个关于求解线性方程组的定理[1][2][3]。该法则适用于变量和方程数目相等的线性方程组,可以通过计算行列式来求解方程组的所有解。它由瑞士数学家克莱姆(Gabriel Cramer)于1750年在他的《线性代数分析导言》中发表。↩︎
克莱姆法则的基本思想是将每个未知量对应的系数和常数项分别构成一个新的矩阵,然后计算该矩阵的行列式和各个元素的代数余子式,最后用这些值来表示每个未知量的解。 梯形电路代表一种常用的电路样式, 完全基于串联和并联连接进行配置。
 ↩︎
↩︎这里不用大写是因为这里有可能是时变的 ↩︎