线性时间排序算法：基数排序

 一、基本原理

基数排序是基于计数排序的，基数排序着眼于输入序列的每一位数，每一轮排序都是根据序列中的某一位数进行排序，从低位到高位各进行一次这种排序思想，最终序列便是有序的。由于输入序列每一位数都是有限的，比如十进制序列，每位数都是0~9的数字，于是可以选择计数排序对序列某一位数进行排序。同样，基数排序也不能处理非负数。

二、图解思考过程

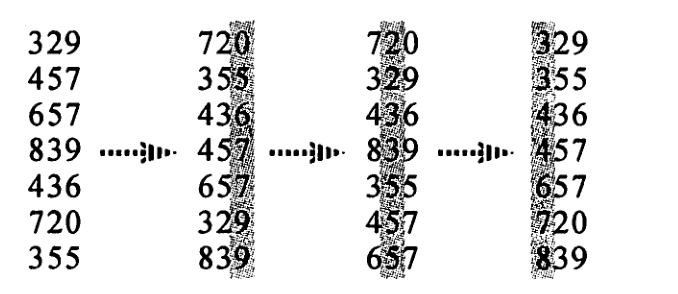
 三、实现代码

import random

def list_to_buckets(li,iteration):
    """
    :param li: 列表
    :param iteration: 装桶是第几次迭代
    :return:
    """
    buckets = [[] for _ in range(10)]
    for num in li:
        digit = (num // (10 ** iteration)) % 10
        buckets[digit].append(num)
    return buckets

def buckets_to_list(buckets):
    return [num for bucket in buckets for num in bucket]


def radix_sort(li):
    maxval = max(li) #10000
    it = 0
    while 10 ** it <= maxval:
        li = buckets_to_list(list_to_buckets(li,it))
        it += 1
    return  li

li = [random.randint(0,100) for _ in range(100)]
print(radix_sort(li))

输出结果

"C:\Program Files\Python35\python.exe" E:/python/test/radix_sort.py
[1, 2, 3, 3, 4, 4, 7, 7, 7, 8, 8, 12, 12, 13, 14, 15, 16, 17, 18, 18, 19, 21, 23, 23, 24, 24, 25, 25, 25, 27, 28, 29, 29, 29, 32, 32, 32, 33, 34, 34, 36, 37, 39, 40, 41, 42, 43, 43, 45, 46, 51, 52, 52, 54, 57, 59, 61, 61, 64, 66, 67, 67, 68, 68, 68, 70, 71, 71, 72, 73, 73, 73, 74, 75, 75, 76, 77, 77, 77, 79, 81, 82, 83, 84, 86, 86, 88, 91, 91, 92, 92, 93, 93, 95, 96, 96, 96, 96, 97, 98]

Process finished with exit code 0

 

四、性能分析

1、时间复杂度

• 时间复杂度：O(n)O(n)
• 空间复杂度：O(n)O(n)
• 是否稳定：是
• 应用场景：同计数排序

2、应用场景

计数排序虽然时间复杂度较低，但需要满足的条件较多，如果能满足限制条件与空间需求，计数排序自然很快