数据结构与算法之美学习笔记：第二十八讲

一、如何理解堆

1、堆是一个完全二叉树

2、大顶堆

对于每个节点的值都大于等于子树中每个节点值的堆

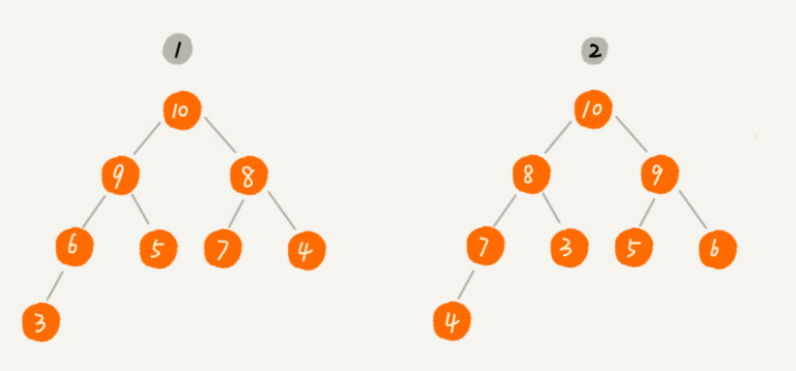
3、小顶堆

对于每个节点的值都小于等于子树中每个节点值的堆

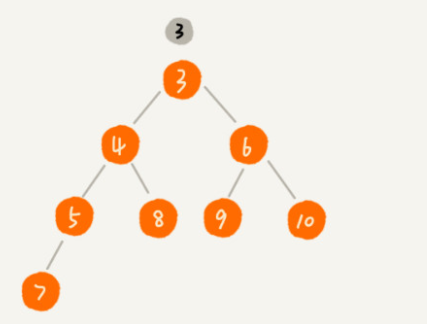
 二、如何实现一个堆

1、如何存储一个堆

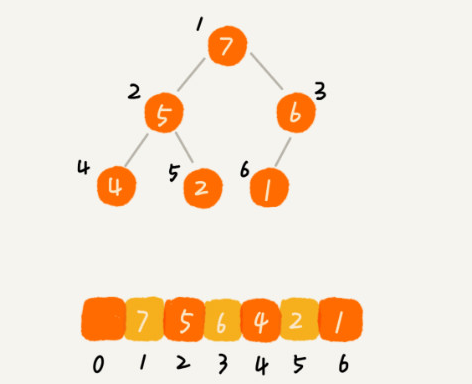
 从图中我们可以看到：
1、数组中下标为 i 的节点的左子节点，就是下标为 i∗2 的节点，
2、右子节点就是下标为 i∗2+1 的节点，父节点就是下标为 i2 的节点。

2、往堆中插入一个元素

1、堆化

2、从下往上的堆化方法

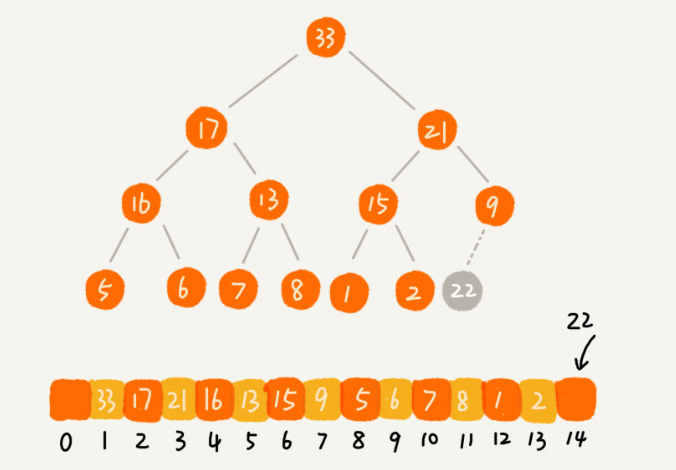
 让新插入的节点与父节点对比大小

1、让新插入的节点与父节点对比大小
2、如果不满足子节点小于等于父节点的大小关系、我们就互换两个节点
3、一直重复这个过程，直到父子节点之间满足刚说的那种大小关系。 

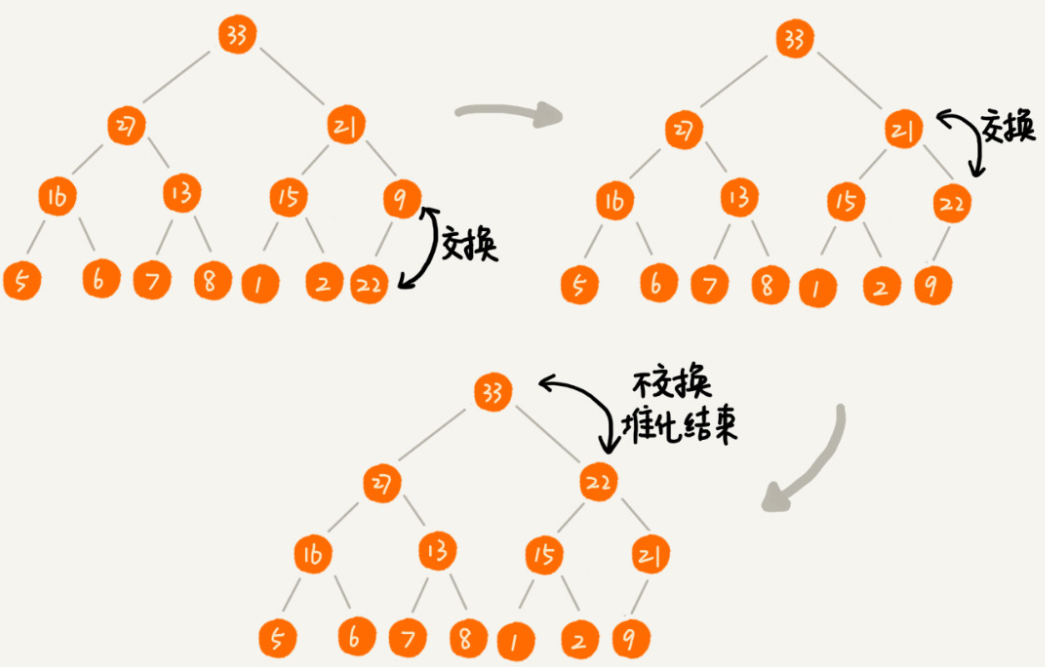
3、删除堆顶元素

从上往下的堆化方法

 4、复杂度分析

三、 如何基于堆实现排序？

1、堆排序过程：

1.建立堆。
2.得到堆顶元素，为最大元素
3.去掉堆顶，将堆最后一个元素放到堆顶，此时可通过⼀一次调整重新使堆有序。
4.堆顶元素为第二大元素。
5.重复步骤3，直到堆变空。

2、堆排序实现

def sift(li, low, high):
    """
    :param li: 列表
    :param low: 堆的根节点位置
    :param high: 堆的最后一个元素的位置
    :return:
    """
    i = low # i最开始指向根节点
    j = 2 * i + 1 # j开始是左孩子
    tmp = li[low] # 把堆顶存起来
    while j <= high: # 只要j位置有数
        if j + 1 <= high and li[j+1] > li[j]: # 如果右孩子有并且比较大
            j = j + 1  # j指向右孩子
        if li[j] > tmp:
            li[i] = li[j]
            i = j           # 往下看一层
            j = 2 * i + 1
        else:       # tmp更大，把tmp放到i的位置上
            li[i] = tmp     # 把tmp放到某一级领导位置上
            break
    else:
        li[i] = tmp  # 把tmp放到叶子节点上


def heap_sort(li):
    n = len(li)
    for i in range((n-2)//2, -1, -1):
        # i表示建堆的时候调整的部分的根的下标
        sift(li, i, n-1)
    # 建堆完成了
    for i in range(n-1, -1, -1):
        # i 指向当前堆的最后一个元素
        li[0], li[i] = li[i], li[0]
        sift(li, 0, i - 1) #i-1是新的high

3、图解堆堆化代码

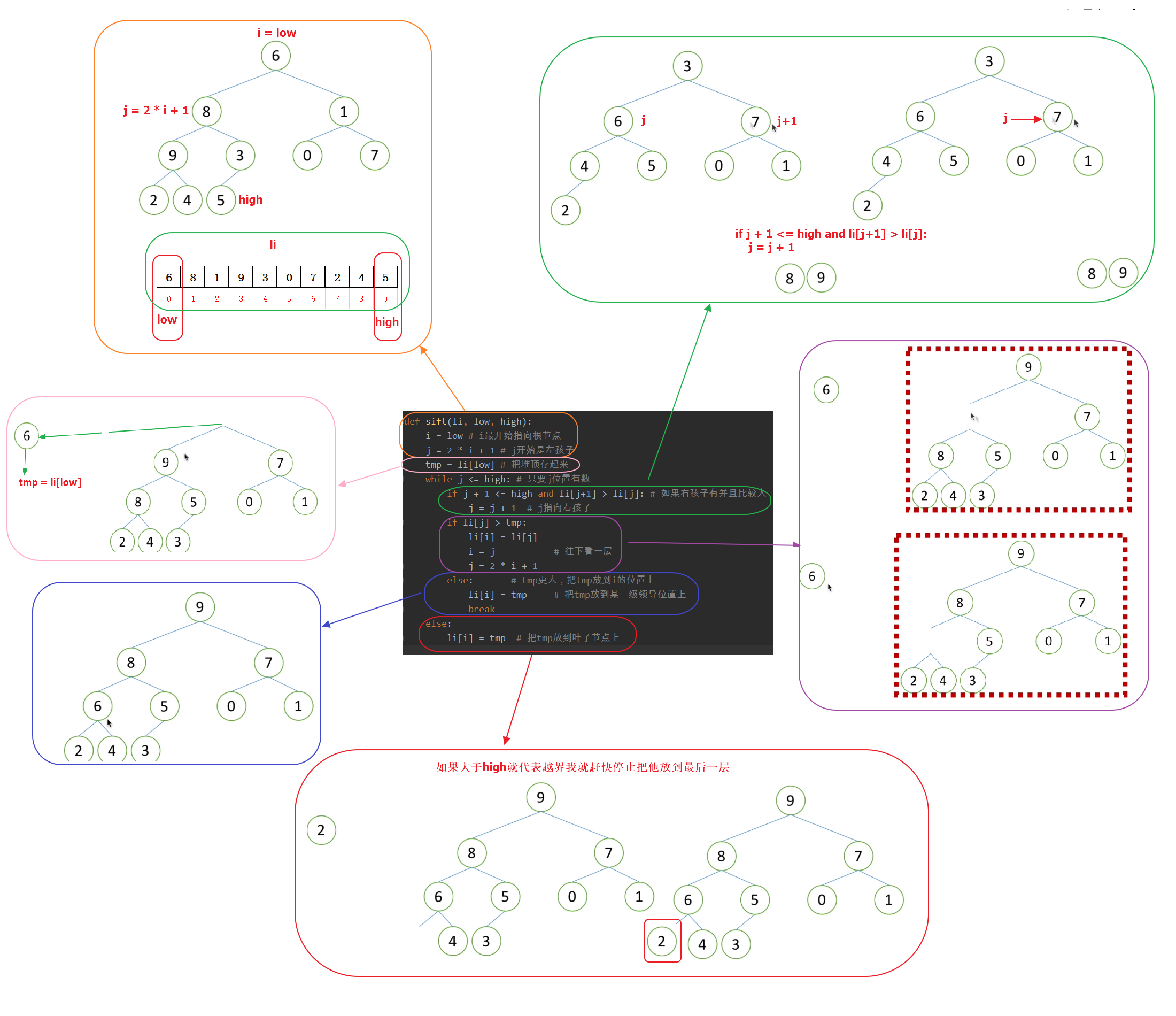
4、图解堆排序代码