数据结构与算法之美学习笔记：第十五讲

一、课前问题

今天我们讲一种针对有序数据集合的查找算法：二分查找（Binary Search）算法，也叫折半查找算法。二分查找的思想非常简单，很多非计算机专业的同学很容易就能理解，
但是看似越简单的东西往往越难掌握好，想要灵活应用就更加困难。老规矩，我们还是来看一道思考题。

假设我们有1000万个整数数据，每个数据占8个字节，如何设计数据结构和算法，快速判断某个整数是否出现在这1000万数据中？ 我们希望这个功能不要占用太多的内存空间，
最多不要超过100MB，你会怎么做呢？带着这个问题，让我们进行今天的内容吧！

二、无处不在的二分思想

二分查找是一种非常简单易懂的快速查找算法，生活中到处可见。比如说，我们现在来做一个猜字游戏。我随机写一个0到99之间的数字，然后你来猜我写的是什么。猜的过程中，
你每猜一次，我就会告诉你猜的对了还是错了，直到猜中为止。你来想想，如何快速猜中我写的数字呢？

假设我写的数字是23，你可以按照下面的步骤来试一试。（如果猜测范围的数字有偶数个，中间数有两个，就选择较小的那个。）

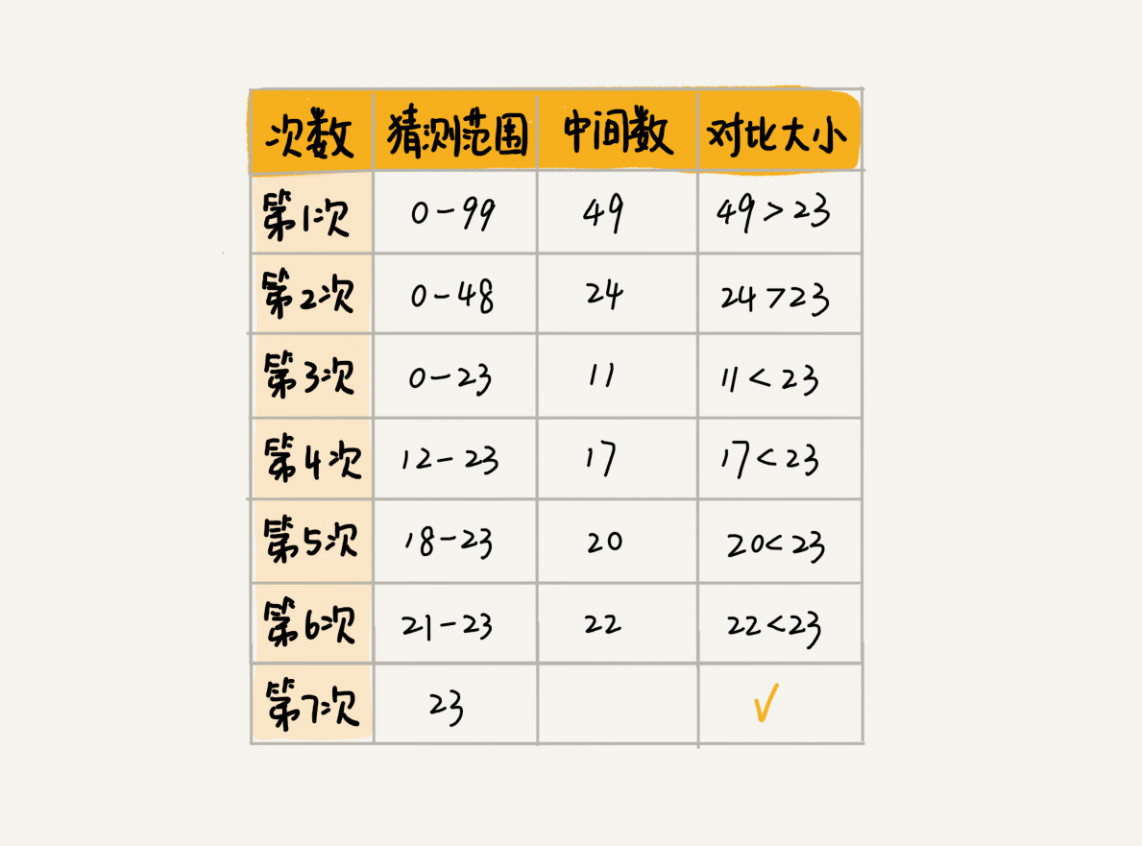
• 7次就猜出来了，是不是很快？这个例子用的就是二分思想，
• 按照这个思想，即便我让你猜的是0到999的数字，最多也只要10次就能猜中。不信的话，你可以试一试。

这是一个生活中的例子，我们现在回到实际的开发场景中。

• 假设有1000条订单数据，已经按照订单金额从小到大排序，
• 每个订单金额都不同，并且最小单位是元。
• 我们现在想知道是否存在⾦金额等于19元的订单。
• 如果存在，则返回订单数据，如果不存在则返回null。

最简单的办法当然是从第一个订单开始，一个一个遍历这1000个订单，

直到找到金额等于19元的订单为止。但这样查找会比较慢，最坏情况下，可能要遍历完这1000条记录才能找到。

那用二分查找能不能更快速地解决呢？

为了方便讲解，我们假设只有10个订单，订单金额分别是：8，11，19，23，27，33，45，55，67，98。

• 还是利用二分思想，每次都与区间的中间数据比对大小，
• 缩小查找区间的范围。为了更加直观，

我画了一张查找过程的图。其中，low和high表示待查找区间的下标，mid表示待查找区间的中间元素下标。

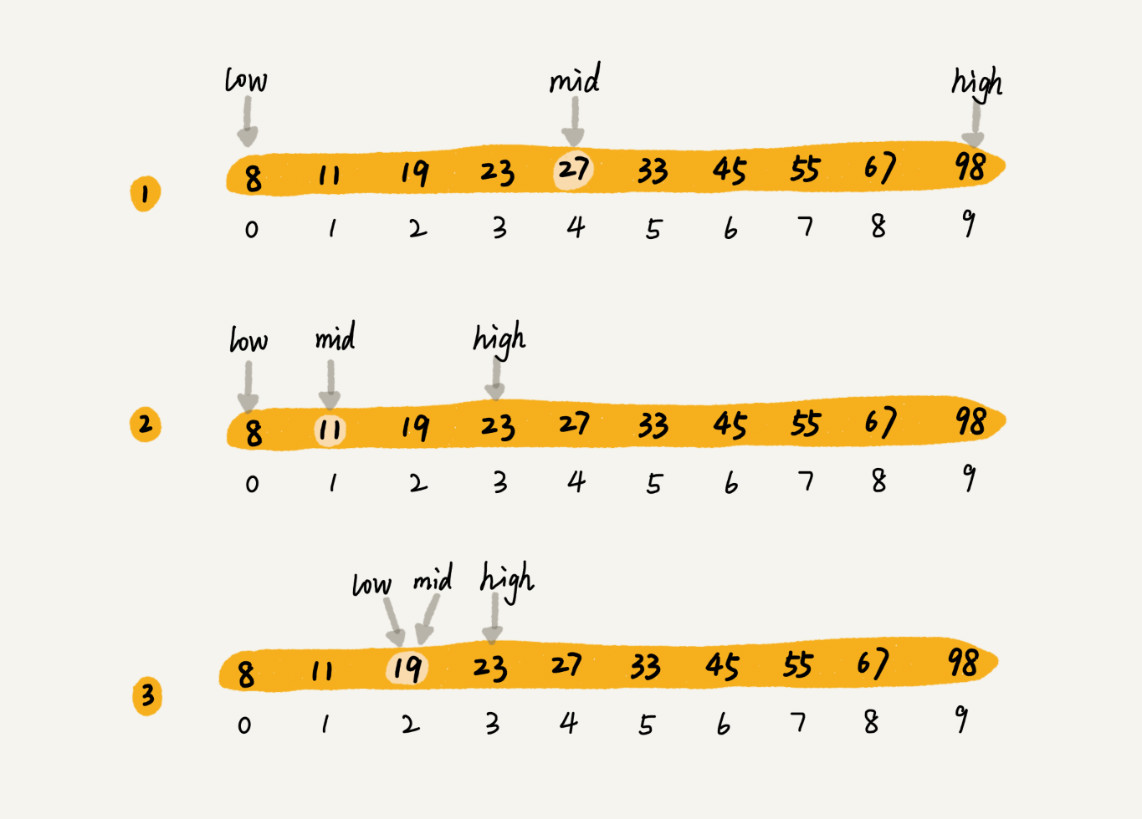
看懂这两个例子，你现在对二分的思想应该掌握得妥妥的了。我这里稍微总结升华一下，

• 二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。
• 每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为0。

三、O(logn)惊人的查找速度

二分查找是一种非常高效的查找算法，高效到什么程度呢？我们来分析一下它的时间复杂度。

我们假设数据大晓是n，每次查找后数据都会缩小为原来的一半，也就是会除以2。最坏情况下，直到查找区间被缩小为空，才停来。

可以看出来，这是一个等比数列。其中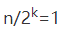时，k的值就是总共缩小的次数。而每一次缩小操作只涉及两个数据大小的比较，所以，经过了k次区间缩⼩操作，

通过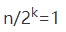，我们可以求得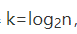，所以时间复杂度就是O(logn)。时间复杂度就是O(k)

O(logn)是一种极其高效的时间复杂度

• 二分查找是我们目前为止遇到的第一个时间复杂度为O(logn)的算法。
• 后面章节我们还会讲堆、二叉树的操作等等，它们的时间复杂度也是O(logn)。

我这里就再深入地讲O(logn)这种对数时间复杂度。这是一种极其高效的时间复杂度，有的时候甚至比时间复杂度是常量级O(1)的算法还要高效。为什么这么说呢？

因为logn是一个非常“恐怖”的数量级，即便n非常非常大，对应的logn也很小。比如n等于2的32次方，这个数很大了吧？大约是42亿。也就是说，
如果我们在42亿个数据中用二分查找一个数据，最多需要比较32次。

我们前面讲过，用大O标记法表示时间复杂度的时候，会省略掉常数、系数和低阶。对于常量级时间复杂度的算法来说，O(1)有可能表示的是一个非常大的常量值，比如O(1000)、O(10000)。所以，
常量级时间复杂度的算法有时候可能还没有O(logn)的算法执行效率高。

反过来，对数对应的就是指数。有一个非常著名的“阿基米德与国王下棋的故事”，你可以自行搜索一下，感受一下指数的“恐怖”。这也是为什么我们说，
指数时间复杂度的算法在小规模数据面前是我无效的。

四、二分查找的递归与非递归实现

实际上，简单的二分查找并不难写，注意我这里的“简单”二字。下一节，我们会讲到二分查找的变体问题，那才是真正烧脑的。今天，我们来看如何来写最简单的二分查找。

最简单的情况就是有序数组中不存在重复元素，我们在其中用二分查找值等于给定值的数据。我用Java代码实现了一个最简单的二分查找算法。

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;

  while (low <= high) {
    int mid = (low + high) / 2;
    if (a[mid] == value) {
      return mid;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }

  return -1;
}

这个代码我稍微解释一下：

• low、high、mid都是指数组下标，其中low和high表示当前查找的区间范围，
• 初始low=0， high=n-1。mid表示[low, high]的中间位置。我们通过对比a[mid]与value的大小，来更新接下来要查找的区间范围，
• 直到找到或者区间缩小为0，就退出。

如果你有一些编程基础，看懂这些应该不成问题。现在，我就着重强调一下容易出错的3个地方。

1、循环退出条件

注意是low<=high，而不是low<high。

2、mid的取值

• 实际上，mid=(low+high)/2这种写法是有问题的。因为如果low和high比较大的话，两者之和就有可能会溢出。
• 改进的方法是将mid的计算公式写成low+(high-low)/2。
• 更进一步，如果要将性能优化到极致的话，我们可以将这⾥的除以2操作转化成位运算low+((high-low)>>1)。

因为相比除法运算来说，计算机处理位运算要快得多。

3、low和high的更新

• low=mid+1，high=mid-1。注意这里的+1和-1，
• 如果直接写成low=mid或者high=mid，就可能会发生死循环。
• 比如，当high=3，low=3时，如果a[3]不等于value，就会导致一直循环不退出。

如果你留意我刚讲的这三点，我想一个简单的二分查找你已经可以实现了。实际上，二分查找除了用循环来实现，还可以用递归来实现，过程也非常简单。

我用Java语言实现了一下这个过程，正好你可以借此机会回顾一下写递归代码的技巧。

// 二分查找的递归实现
public int bsearch(int[] a, int n, int val) {
  return bsearchInternally(a, 0, n - 1, val);
}

private int bsearchInternally(int[] a, int low, int high, int value) {
  if (low > high) return -1;

  int mid =  low + ((high - low) >> 1);
  if (a[mid] == value) {
    return mid;
  } else if (a[mid] < value) {
    return bsearchInternally(a, mid+1, high, value);
  } else {
    return bsearchInternally(a, low, mid-1, value);
  }
}

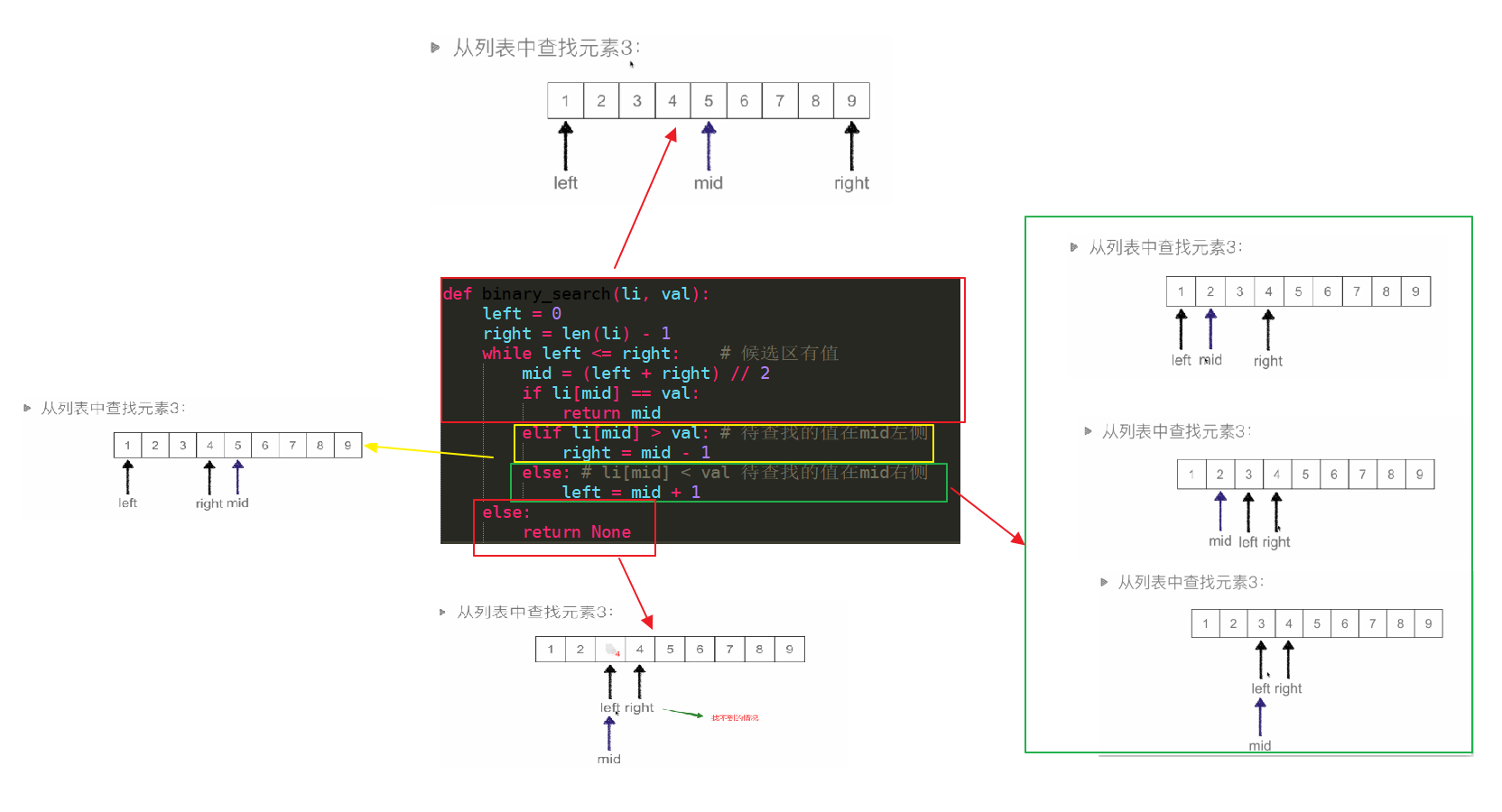
python实现代码

def binary_search(li, val):
    left = 0
    right = len(li) - 1
    while left <= right:    # 候选区有值
        mid = (left + right) // 2
        if li[mid] == val:
            return mid
        elif li[mid] > val: # 待查找的值在mid左侧
            right = mid - 1
        else: # li[mid] < val 待查找的值在mid右侧
            left = mid + 1
    else:
        return None

代码图解

五、二分查找应用场景的局限性

前面我们分析过，二分查找的时间复杂度是O(logn)，查找数据的效率非常高。不过，并不是什么情况下都可以用二分查找，它的应用场景是有很局局限性的。

那什么情况下适合用二分查找，什么情况下不适合呢？

1、首先，二分查找依赖的是顺序表结构，简单点说就是数组

那二分查找能否依赖其他数据结构呢？

比如链表。答案是不可以的，主要原因是二分查找算法需要按照下标随机访问元素。我们在数组和链表那两节讲过，数组按照下标随机访问数据的时间复杂度是O(1)，
而链表随机访问的时间复杂度是O(n)。所以，如果数据使用链表存储，二分查找的时间复杂就会变得很大。

二分查找只能用在数据是通过顺序表来存储的数据结构上。如果你的数据是通过其他数据结构存储的，则无法应用二分查找。

2、其次，二分查找针对的是有序数据

二分查找对这一点的要求比较苛刻，数据必须是有序的。如果数据没有序，我们需要先排序。前面章节里我们讲到，排序的时间复杂度最低是O(nlogn)。所以，如果我们针对的是一组静态的数据，
没有频繁地插入、删除，我们可以进行一次排序，多次二分查找。这样排序的成本可被均摊，二分查找的边际成本就会比较低。

但是，如果我们的数据集合有频繁的插入和删除操作，要想用二分查找，要么每次插入、删除操作之后保证数据仍然有序，要么在每次二分查找之前都先进行排序。针对这种动态数据集合，
无论哪种一法，维护有序的成本都是很大的。

所以，二分查找只能用在插入、删除操作不频繁，一次排序多次查找的场景中。针对动态变化的数据集合，二分查找将不再适合。那针对动态数据集合，
如何在其中快速查找某个数据呢？别急，等到二叉树那一节我会详细讲。

3、再次，数据量太小不适合二分查找。

如果要处理的数据量很小，完全没有必要用二分查找，顺序遍历就足够了。比如我们在一个大小为10的数组中查找一个元素，不管用二分查找还是顺序遍历，查找速度都差不多。
只有数据量比较大的时候，二分查找的优势才会比较明显。

不过，这里有一个例外。如果数据之间的比较操作非常耗时，不管数据量大小，我都推荐使用二分查找。比如，数组中存储的都是长度超过300的字符串，如此大的两个字符串之间的对比大小，就会非常耗时。我们需要尽可能地减少比较次数，二比较次数的减少会大大提高性能，这个时候二分查找就比顺序遍历更有优势。

4、最后，数据量太不也不适合二分查找。

二分查找的底层需要依赖数组这种数据结构，二数组为了只持随机访问的特性，要求内存空间连续，对内存的要求比较苛刻。

比如，我们有1GB大小的数据，如果希望用数组来存储，那就需要1GB的连续内存空间。

注意这的的“连续”二字，也就是说，即便有2GB的内存空间剩余，但是如果这剩余的2GB内存空间都是零散的，没有连续的1GB大小的内存空间，那照样无法申请一个1GB大小的数组。
而我们的二分查找是作用在数组这种数据结构之上的，所以太大的数据用数组存储就比较吃里了，也就不能用二分查找了。

六、解答开篇

二分查找的理论知识你应该已经掌握了。我们来看下开篇的思考题：

如何在1000万个整数中快速查找某个整数？

• 这个问题并不难。我们的内存限制是100MB，每个数据大小是8字节，最简单的办法就是将数据存储在数组中，
• 内存占用差不多是80MB，符合内存的限制。借助今天讲的内容，我们可以先对这1000万数据从小到大排序，
• 然后再利用二分查找算法，就可以快速地查找想要的数据了。

看起来这个问题并不难，很轻松就能解决。实际上，它暗藏了“玄机”。

如果你对数据结构和算法有一定了解，知道散列表、二叉树这些支持快速查找的动态数据结构。你可能会觉得，用散列表和二叉树也可以解决这个问题。实际上是不对的。

• 虽然大部分情况下，用二分查找可以解决的问题，但散列表、二叉树都可以解决。
• 但是，我们后面会讲，不管是散列表还是二叉树，都会需要比较多的额外的内存空间。
• 如果用散列表或者二叉树来存储这1000万的数据，用100MB的内存肯定是存不下的。
• 用二分查找底层依赖的是数组，除了数据本身之外，不需要额外存储其他信息，是最省内存空间的存储方式，

所以刚好能在限定的内存大小下解决这个问题。

七、内容小结

今天我们学习了一种针对有序数据的高效查找算法，二分查找，它的时间复杂度是O(logn)。

二分查找的核心思想理解起来非常简单，有点类似分治思想。即每次都通过跟区间中的中间元素对比，将待查找的区间缩小为一半，直到找到要查找的元素，或者区间被缩小为0。但是二分查找的代码实现比较容易写错。你需要着重掌握它的三个容易出错的地方：

• 循环退出条件
• mid的取值
• low和high的更新。

二分查找虽然性能比较优秀，但应用场景也比较有限。

• 底层必须依赖数组，
• 并且还要求数据是有序的。对于较小规模的数据查找，我们直接使用顺序遍历就可以了，二分查找的优势并不明显。
• 二分查找更适合处理静态数据，也就是没有频繁的数据插入、删除操作。

八、课后思考

1. 如何编程实现“求一个数的平方根”？要求精确到小数点后6位。

经典留言蒋礼锐

因为要精确到后六位，可以先用二分查找出整数位，然后再二分查找小数第一位，第二位，到第六位。

整数查找很简单，判断当前数小于+1后大于即可找到，

小数查找举查找小数后第一位来说，从x.0到(x+1).0，查找终止条件与整数一样，当前数小于，加0.1大于，

后面的位数以此类推，可以用x*10^(-i)通项来循环或者递归，终止条件是i>6，

想了一下复杂度，每次二分是logn，包括整数位会查找7次，所以时间复杂度为7logn。空间复杂度没有开辟新的储存空间，空间复杂度为1。

没有具体用代码实现，只是思路，还请多多指正。之后会用js去实际实现。

2. 我刚才说了，如果数据使用链表存储，二分查找的时间复杂就会变得很大，那查找的时间复杂度究竟是多少呢？如果你自己推导一下，你就会深刻地认识到，为何我们会选择数数组而不是链表来实现二分查找了。

经典留言Jerry银银

说说第二题吧，感觉争议比较大:
假设链表长度为n，二分查找每次都要找到中间点(计算中忽略奇偶数差异):
第一次查找中间点，需要移动指针n/2次；
第二次，需要移动指针n/4次；
第三次需要移动指针n/8次；
......
以此类推，一直到1次为值

总共指针移动次数(查找次数) = n/2 + n/4 + n/8 + ...+ 1，这显然是个等比数列，根据等比数列求和公式：Sum = n - 1.

最后算法时间复杂度是：O(n-1)，忽略常数，记为O(n)，时间复杂度和顺序查找时间复杂度相同

但是稍微思考下，在二分查找的时候，由于要进行多余的运算，严格来说，会比顺序查找时间慢