大素数判断算法 Miller_Rabin

引言：

如果你遇见很多个非常大的数n，有10的18次方这么大，让你来判断是不是素数，你有什么快速的方法呢？

用普通的判断会超时，用筛法又筛不到，这时候就可以用上大素数判断算法。

（其实这个算法理解原理后很简单，我也就wa了11次）

---

 

原理部分：

首先我们知道，对于一个质数P，他一定满足费马小定理，

  即   a^(p-1)≡1(mod p)

那么我们反过来想，对于任意一个数n，若它满足 a^(n-1)≡1(mod n)，那么它是不是就是一个质数呢?

答案是 不一定，但是 在绝大多数的状况下，n就是个质数。因此，对于一个很大的数n，我们可以随便取一个a,然后用

快速幂计算a^(n-1)mod n,看最后的结果是不是1，以此来判断是不是质数。

但这样还是有很大的误差，为此我们引入一个新定理——二次探测原理。

若P是一个质数，且满足0<x<p、x^2 mod p =1，则可以推断出x一定等于1或p-1。

因为除了2，所有的质数都是奇数，所以n若是偶数且不为2，那他一定不是质数，若他是奇数，则（n-1）一定是偶数,

我们就可以把a^(n-1)改写成(a^{^(n-1)/2})²,就满足了二次探测原理的x^2的形式，我们就可以用二次探测原理来验证n是不是质

数，即若x^2%n=1,但x不等于1或n-1，则n一定不是一个质数。

更关键的是，若（n-1）/2仍是一个偶数，我们还可以把a^{^(n-1)/2}改写乘某个数的平方，以此类推。

即把n-1化为2^s * d  ,   a^(n-1)=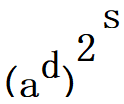

 

 

 

 

 

我们就可以在求 a^(n-1)mod n的过程中，多次验证二次探测原理。

通过上面两个原理，我们再多用几个a验证，判断n是不是质数准确率就可以达到99.9999999999999....%。

另外有一个结论：如果我们选择2,3,7,61,24251,9875321这6个质数作为a的话，在10^14内不存在误判。

好了，如果没有看懂上面的的理论就看下面的代码吧。

---

 代码部分：

inline LL quick_mul(LL a,LL b,LL m) //快速乘 
{
    ll ans = 0;
    a %= m;
    b %= m;
    while (b) {
        if (b & 1) {
            ans = (ans + a) % m;
        }
        a = (a + a) % m;
        b >>= 1;
    }
    return ans;
}

LL quick_pow(LL a,LL b,LL m) //快速幂 
{
    LL res=1;
    a%=m;
    while(b)
    {
        if(b&1) res=quick_mul(res,a,m);
        a=quick_mul(a,a,m);
        b>>=1;
    }
    return res;
}
bool Miller_rabin(LL n,int num)
{
//先将特殊情况判断一下
    if(n==2||n==3) return true;
    if(n%2==0||n==1) return false;
    srand((unsigned)time(NULL)); //为接下来a的随机取值用 
    LL d=n-1;
    int s=0;
    while(!(d&1)) s++,d>>=1;//若d的二进制的最后一位不是1，则说明d还是偶数 
    for(int i=0;i<num;i++)
    {
        LL a=rand()%(n-2)+2;//2~n-1;
        LL x=quick_pow(a,d,n), y=0;
        for(int j=0;j<s;j++)//一共平方s次 
        {
            y=quick_mul(x,x,n);//先平方 
            if(y==1&&x!=1&&x!=(n-1)) return false;//验证二次探测原理 
            x=y;
        }
        if(y!=1) return false;//不满足费马小定理，那就肯定不是质数
    }
    return true;
}

另外补充一点就是，对于上面的快速乘，还有一种更快速的写法

inline LL quick_mul(LL a,LL b,LL m)
{
    LL t=(ld)a/m*b;
    LL res=(ull)a*b-(ull)t*m;
    return (res+m)%m;
}

利用的是 相乘溢出的是高位，但由于取模我们只需要的是低位。

还有就是a*b%m=a*b-(a*b/m)*m