平方根倒数快速算法
平方根是什么?
给定一个,我想算,就是在算平方根
在计算机里最常见的算法是牛顿迭代法
平方根倒数是什么?
给定一个,我想算,就是在算平方根的倒数
平时我们是如何计算的?
如果在纸上写,就是一步一步的算,先算平方根(一般就是查表法),再求倒数;
但是大部分的数是无法在表格上查找到的
所以,这个快速算法是非常高效的
怎么个快速法?
计算机中的浮点数#
- 假设一个数是浮点数Y
我们可能不太清楚,它在计算机是如何存储的,但是这就是这个算法的牛逼之处,所以我尽量让大伙明白
eg:浮点数:00111111111000000000000000000000,我们要怎么看? - 首先将浮点数分成这样0 0111 1111 1100 0000 0000 0000 0000 000
其中第一位是符号位(0是正数,1是负数),再过来的八位数(科学记数法里的指数位),再过来23位(科学计数法的有效位数,有效位数就是指小数点前不能为0,且只能有1位,所以第一个位的范围就是1~9)
- 好,那么好,这个数是不是就是1100 0000 0000 0000 0000 000 *10^(0111 1111)呢?
答案是,错误;这个E的范围其实是-127~128,因为我们知道,在指数上面的负号不是说数字是负数,而是指小数点前有几个零
那个M也是错的,之前都说了他只有代表1~9之前的数,然后后面是小数点位数,怎么会是1111 1100 0000 0000 0000 0000 000
我们考虑一下,如果我们用二进制的科学记数法去表示数,那么我们的有效位数是不是就变成了1.xxxxx,
而xxxxx都是由0跟1组成的序列,那么好,其实M记录的就是xxxxx序列,
所以其实是1.1100 0000 0000 0000 0000 000 * 2^(0111 1111 - 0111 1111),
这里减0111 1111就是为了让E的范围是-127~128,
所以十进制为1.1100 0000 0000 0000 0000 000 * 2^(0111 1111 - 0111 1111)=1.75 * 2 ^ 0 = 1.75
我们可以得出一个公式,这是一个十进制表示的公式,这里有疑问的同学可以自己去搜一下为什么是这个表达式
如果你不想搜,我可以给你一个方向,把这题搞明白就知道了----->“我有10个箱子,箱子需要放苹果,此时,我想用10个箱子去表示0~ 1000数量的苹果,请问这些箱子我要如何去放苹果才能用这些箱子表示0~1000之间任意数量的苹果”(答案:1 2 4 16 32 64 128 256 512这样子装就行)
对数#
好嘞,看完,我们开始
- 给你一个,你要算出,我们假设 = ,
取对数,问题转到了计算机如何算一个数 - 用刚刚的公式:得,
,
其中很小,所以利用近似思想,
,这样就将运算,转成了除法跟乘法了
但是细心的同学们会发现这个形式跟浮点数的公式好像,可不可以转成浮点数的样子呢? - ,这个相当于左移了23位,刚好跟浮点数的对上,这里加减不能用浮点数运算去理解,得用整数运算理解,所以,是存储在计算机中的浮点数格式,如果这个数字按整数解读是一个相当大的数字
所以也是一样的,所以,是存储在计算机中的浮点数格式
得到等式:,现在问题转变成了求解A是什么数
,是存储在计算机中的浮点数格式, =
就是存储在计算机中的浮点数格式,得到的就是一个近似解
总结:从开始的 = ,转成了计算机如何算一个数,然后将运算转成了线性运算,到最后问题转变成了求解,是存储在计算机中的浮点数格式
注意:我这里忽略了符号位的计算
代码
//部分示例
int ksqrt (float num) {
int const_num = 0x5F400000; //这里可以改成0x5f3759df,答案更精确
float y = num;
int i = * (int *) &y; //将y转成int 类型运算
int a = const_num - (i >> 1);//右移奇数,会少了小数,相当于整除
y = * (float*) &a;//把a变回浮点数
//一步牛顿迭代法就够了
//牛顿迭代的步骤
//xn+1 = xn - f(xn) / f'(xn)
//f(x)如何构建?
//y = a ^ -(1/2)
//y^-(1/2) = a
//y^-(1/2) - a = 0
//构建一个f(y) = 1 / y^2 - a
//f(x) = 1/ x^2 - a
y = 1.5*y - (num * 0.5) * y * y * y;
return y;
}
总结
这个思想最牛的地方就是将运算转成了近似的线性运算,使得平方根倒数的求解变的简单,牛顿迭代如果最初点选择的好,就会使得运算大大减少,多思考多学习,勉励;


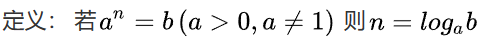
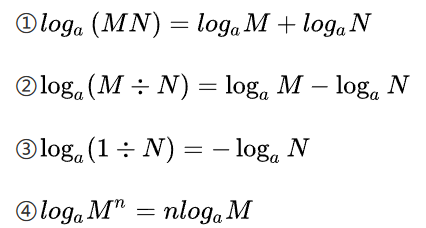



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具