代码随想录----做题篇----二分法
ABOUT
只做题,想思路
二分法
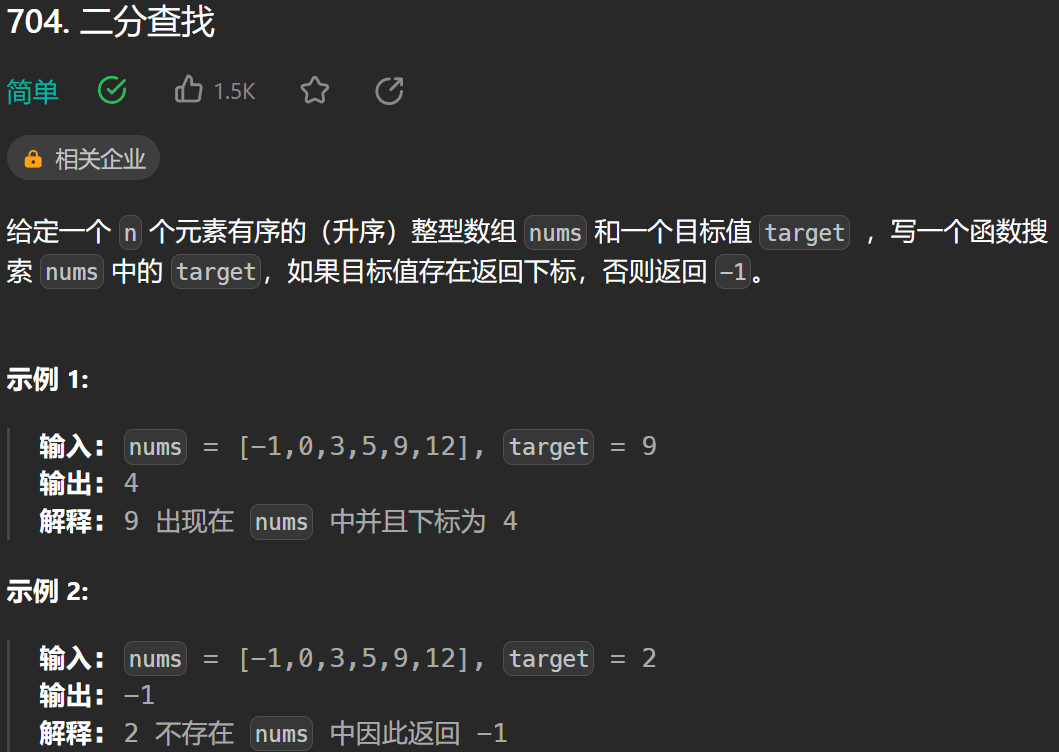
思路:两端的平均数跟要找的值对比,小了就缩小左边区间,大了就缩小右边区间,然后再次求两端的平均数,小了就缩小左边区间,大了就缩小右边区间,最终到达循环结束
- 对比加缩小区间,写法很简单
if (nums[mid] > target){
right = mid;
}
else if (nums[mid] < target){
left = mid;
}
else if (target == nums[mid]){
return mid;
}
- 结束条件呢?
while(left <= right)
or
while(left < right)
- 假设第一种结束条件
while(left <= right) {//一定会存在一种情况就是左右区间取了相同值,这个区间是左闭右闭的
if (nums[mid] > target){
right = mid;
}
else if (nums[mid] < target){
left = mid;
}
else if (target == nums[mid]){
return mid;
}
mid = (left + right) / 2;
//考虑target在最右边,这个写法有问题
//考虑target在最左边,这个写法感觉没有什么问题,但是它循环了三次
}
当我们发现给left = mid; 改成left = mid + 1;最右边的情况解决了,但是最左边的情况还是循环三次;那我们给它right = mid;改成right = mid - 1;循环次数少了一次
why?
你只要画一下图,你就会发现其实mid所指向的那个数根本没有比的必要,所以left = mid + 1;可以,我刚刚说的target就算在最左边其实也可以比到,所以left可以加一;
减一呢?是否是我上面说的减一是为了循环次数少了一次?NONONO,这个减一非常有必要的加上去,不然就会出现死循环,比如target是在0到1之间的数,left跟right最终只会等于1,而无法返回正确结果,虽然我们知道死循环就是无解,就应该返回-1。
所以代码的最终样子是这样的
class Solution {
public:
int search(vector<int>& nums, int target) {
if (0 == nums.size())
return -1;
int left = 0;
int right = nums.size() - 1;
int mid = (left + right) / 2;
if (nums[left] > target)
return -1;
if (nums[right] < target)
return -1;
if (nums[left] == target)
return left;
if (nums[right] == target)
return right;
//这四句是为了提高效率
while(left <= right){
if (nums[mid] > target){
right = mid - 1;
}
else if (nums[mid] < target){
left = mid + 1;
}
else if (target == nums[mid]){
return mid;
}
mid = (left + right) / 2;
}
return -1;
}
};
- 第二种呢?
while(left < right)
经过上面的思考,我们发现不会出现死循环了,因为left < right,所以我们也不需要right = mid -1;
所以最终代码为:
class Solution {
public:
int search(vector<int>& nums, int target) {
if (0 == nums.size())
return -1;
int left = 0;
int right = nums.size() - 1;
int mid = (left + right) / 2;
if (nums[left] > target)
return -1;
if (nums[right] < target)
return -1;
if (nums[left] == target)
return left;
if (nums[right] == target)
return right;
while(left < right){
if (nums[mid] > target){
right = mid;
}
else if (nums[mid] < target){
left = mid + 1;
}
else if (target == nums[mid]){
return mid;
}
mid = (left + right) / 2;
}
return -1;
}
};
扩展题目
1. 搜索插入位置
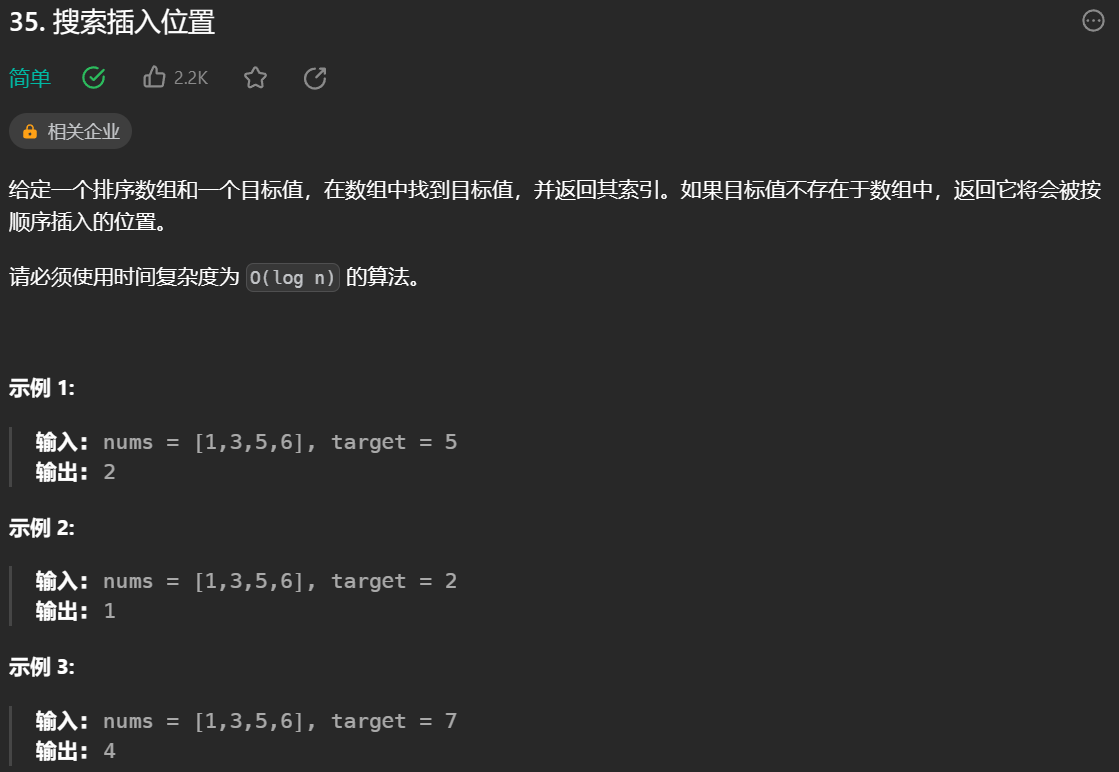
思路:二分法如果找到了就用mid,找不到就需要用到left跟right指针(我习惯叫指针了,但是他们的定义不一定是代码里的指针的定义,这个指针是一个广义上的意思),只要自己举几个例子就知道right + 1一定是找不到而且需要插入的位置,当然需要假设数组没有重复的元素
所以最终代码为:
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int right = nums.size() - 1;
int left = 0;
int mid = (right + left) / 2;
if (target > nums[right])
return (right + 1);
if (target < nums[left])
return left;
while (left <= right) {
if (nums[mid] > target)
right = mid - 1;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] == target)
return mid;
mid = (left + right) / 2;
}
return (right + 1);
}
};
- 在排序数组中查找元素的第一个和最后一个的位置
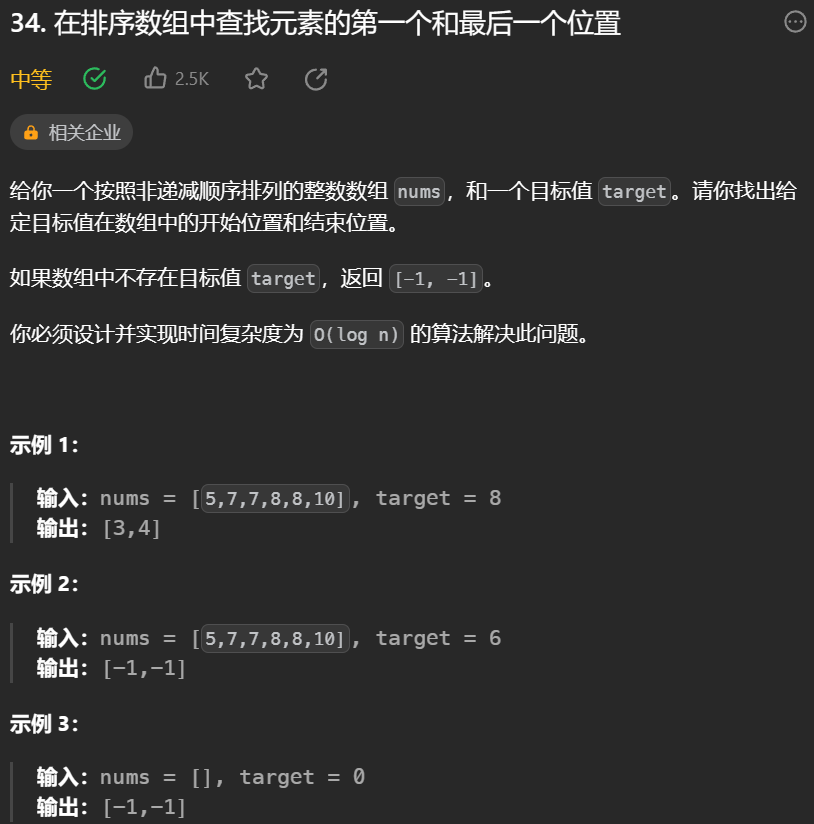
思路:二分法,mid找到的只是target的其中一个,不能确定是最左还是最右边的元素,所以我们还是要利用left_1跟right_1指针,来帮助我们找到左边界与右边界,如何找到?
边界问题
- 考虑越界
- 考虑移动
- 考虑优化
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> return_vector;
if (0 == nums.size()) { //没有元素返回-1,-1
for (int i = 0; i < 2; i++) return_vector.push_back(-1);
return return_vector;
}
int left = 0;
int right = nums.size() - 1;
int mid = (left + right) / 2;
while (left <= right) {
if (nums[mid] > target)
right = mid - 1;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] == target) {
int left_1 = mid;//左边界
int right_1 = mid;//有边界
//while考虑越界问题,if考虑移动问题
while (left_1 - 1 >= 0) {if (nums[left_1 - 1] == target) left_1--;else break;}
while (right_1 + 1 <= nums.size() - 1) {if (nums[right_1 + 1] == target) right_1++;else break;}
return_vector.push_back(left_1);
return_vector.push_back(right_1);
return return_vector;
}
mid = (left + right) / 2;
}
for (int i = 0; i < 2; i++) return_vector.push_back(-1);
return return_vector;
}
};

