516.最长回文子序列 - medium

给定一个字符串 s ，找到其中最长的回文子序列，并返回该序列的长度。可以假设 s 的最大长度为 1000 。

 示例 1:

输入:

"bbbab"
输出:

4
一个可能的最长回文子序列为 "bbbb"。

示例 2:
输入:

"cbbd"
输出:

2
一个可能的最长回文子序列为 "bb"。

 提示：

1 <= s.length <= 1000
s 只包含小写英文字母

 

 

 

 

思路：

　　• 子序列是非连续的，子串是连续的，注意区分；
　　• 最大最小，最长最短，首先想到的就是动态规划，在子串 s[i…j] 中，最长回文子序列为 dp[i][j]，即，在二维数组 dp 中，i,j 的下标表示的是子串的起始终止位置，这个一定要理解；
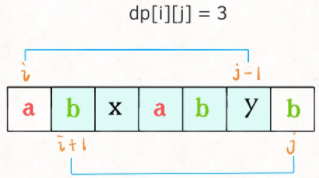
　　• 对于 dp[i][j] , 如果 s[i] == s[j] ，则 d[i][j] = dp[i+1][j-1] + 2，如果 s[i] != s[j] ,则 dp[i][j] = max(dp[i+1][j], dp[i][j-1])；

　　　　　　　　　　　　　　　　

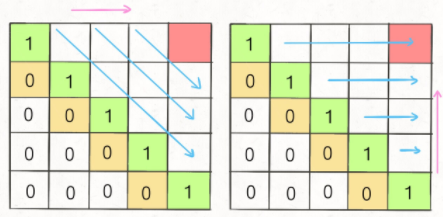
　　• 由于长范围的子串 dp，需要依赖短的子串的结果，所以，先求 dp[n][n]，再求 dp[0][n]，只能斜着或者反着遍历：

　　　　　　　　　　　　

 

 

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        int[][] dp = new int[n][n];
        for(int i = 0; i < n; i++) dp[i][i] = 1; //对角线上的单个元素为1
        for(int i = n-1; i >= 0; i--){
            for(int j = i+1; j < n; j++){ //先得到后面短的字符串，最后才得到全局的结果
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1] + 2; // i，j 是字符串中的位置，所以是 i+1, j-1
                }else dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);
            }
        }
        return dp[0][n-1]; //全部的字符串结果
    }
}