122.Best Time to Buy and Sell Stock II

 

 

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        if length == 0:
            return 0
        minBuyPrice = prices[0]
        maxProfit = 0
        for i in range(1, length):
            if prices[i] < prices[i-1] and prices[i-1] > minBuyPrice:
                maxProfit += prices[i-1] - minBuyPrice
                minBuyPrice = prices[i]
            if prices[i] < minBuyPrice:
                minBuyPrice = prices[i]
        if prices[length-1] > minBuyPrice:
            maxProfit += prices[length-1] - minBuyPrice
        return maxProfit

 

 

 

Java 版：

　　• 贪心算法（方法一）；
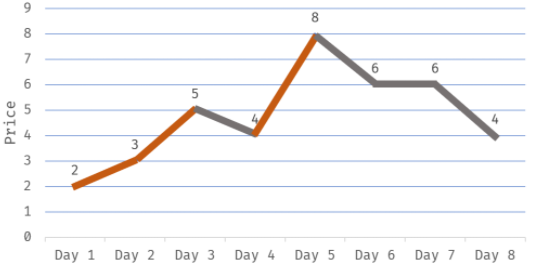
　　• 所有上涨交易日都买卖（相当于上涨第一天买，上涨最后一天卖，只是代码中表现为每一天都既买又卖），所有下降交易日都不买卖，防止亏钱。

　　　　　　　　　　

 

 

class Solution {
    public int maxProfit(int[] prices) {
        int res = 0;
        for (int i = 1; i < prices.length; i++) {
            int tmp = prices[i] - prices[i - 1]; //表示上涨
            if (tmp > 0) res += tmp;
        }
        return res;
    }
}

 

　　• 动态规划（方法二）：
　　• 每一天只能交易一次，所以第 i天要么不持有股票、要么持有股票，只有这两种状态，则用一个二维数组来表示， dp[i][0]表示不持有股票时手里的钱、dp[i][1]表示持有股票且手里剩余的钱；
　　• 最开始，第一天，设手中的钱为 0，即 dp[0][0] = 0，则手中持有股票后剩余的钱为： 0 - prices[0] = -2 ,相当于垫付 2元来买股票，欠股票市场 2 元，先欠着，等后面卖出去后来还；
　　• 第 i天时，dp[i][0]要么继承自dp[i-1][0]，要么为第 i天将之前持有的股票以第 i天的价格抛售卖出后的收益，两者取最大值；
　　• 同理，dp[i][1]要么为继承自 dp[i-1][1]的股票，要么第 i天现买的股票，取买完股票后手中剩余钱最多的；
　　• 手里持有股票，且剩余的钱最多，相当于股票的买入价格越低，也是局部最优的。

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] dp = new int[n][2];
        dp[0][1] = -prices[0]; //持有股票，手里剩余的钱,初始没钱，就是负的
        for(int i = 1; i < n; i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            //dp[i-1][1] + prices[i] 表示上一次手中持有股票且剩余的钱 + 以今天价格抛售能获得的钱
            dp[i][1] = Math.max(dp[i-1][1], dp[i][0] - prices[i]);
            //dp[i][0] - prices[i] 表示以今天的价格prices[i]买入股票后，剩余的钱
        }
        return dp[n-1][0];
    }
}