机器学习笔记(十四)——非线性逻辑回归(sklearn)
本博客仅用于个人学习,不用于传播教学,主要是记自己能够看得懂的笔记(
学习知识、资源和数据来自:机器学习算法基础-覃秉丰_哔哩哔哩_bilibili
用sklearn库就灰常简单啦~
可以自己用make_gaussian_quantiles生成数据。(就不用再把数据搞上来了)
代码:
from sklearn.preprocessing import PolynomialFeatures from sklearn import preprocessing from sklearn import linear_model import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_gaussian_quantiles #生成正态分布的数据,可以设置数量和维度等 x_data,y_data=make_gaussian_quantiles(n_samples=500,n_features=2,n_classes=2) plt.scatter(x_data[:,0],x_data[:,1],c=y_data) plt.show() #首先线性逻辑回归 model=linear_model.LogisticRegression() model.fit(x_data,y_data) w=model.coef_ b=model.intercept_ z=-(b+w[0,0]*x_data[:,0])/w[0,1] plt.scatter(x_data[:,0],x_data[:,1],c=y_data) plt.plot(x_data[:,0],z,'k') plt.show() #求出R^2值,相当于准确率 print(model.score(x_data,y_data)) poly=PolynomialFeatures(degree=3) X_data=poly.fit_transform(x_data) model=linear_model.LogisticRegression() model.fit(X_data,y_data) xmi=x_data[:,0].min()-1 xma=x_data[:,0].max()+1 ymi=x_data[:,1].min()-1 yma=x_data[:,1].max()+1 xx=np.arange(xmi,xma,0.02) yy=np.arange(ymi,yma,0.02) xx,yy=np.meshgrid(xx,yy) z=model.predict(poly.fit_transform(np.c_[xx.ravel(),yy.ravel()])) #求出全图的预测值 z=z.reshape(xx.shape) plt.contourf(xx,yy,z) #等高线图 plt.scatter(x_data[:,0],x_data[:,1],c=y_data) plt.show() print(model.score(X_data,y_data))
得到结果:
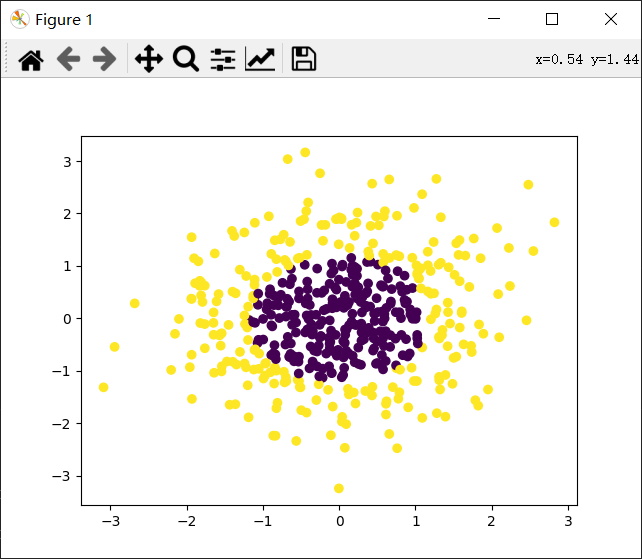
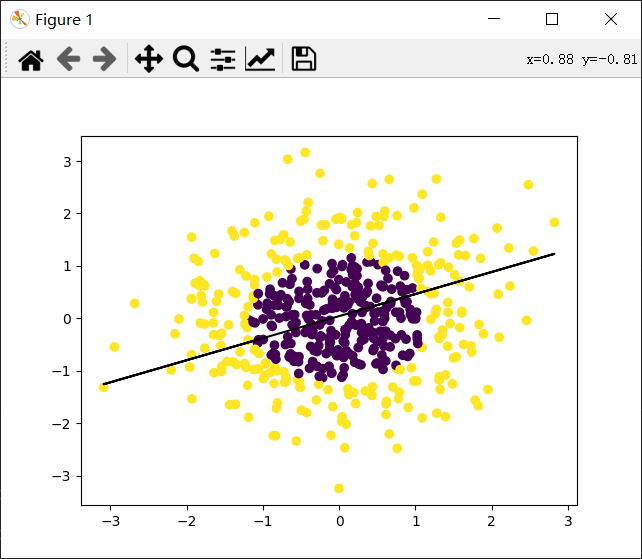
0.538
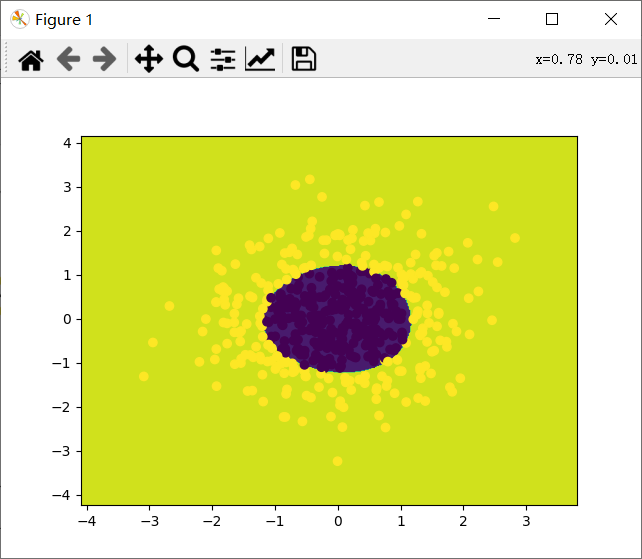
0.994
参考博客:
机器学习算法的随机数据生成 - 刘建平Pinard - 博客园 (cnblogs.com)
sklearn.datasets.make_gaussian_quantiles — scikit-learn 0.24.2 documentation
API解析------------在逻辑回归中predict()与score()的用法_data_curd的博客-CSDN博客




