机器学习笔记（十三）——非线性逻辑回归（梯度下降法）

本博客仅用于个人学习，不用于传播教学，主要是记自己能够看得懂的笔记（

学习知识、资源和数据来自：机器学习算法基础-覃秉丰_哔哩哔哩_bilibili

根据之前的经验，非线性逻辑回归与线性逻辑回归差别不大，只是多了几个特征值，也就是把x矩阵转换为多项式矩阵即可。

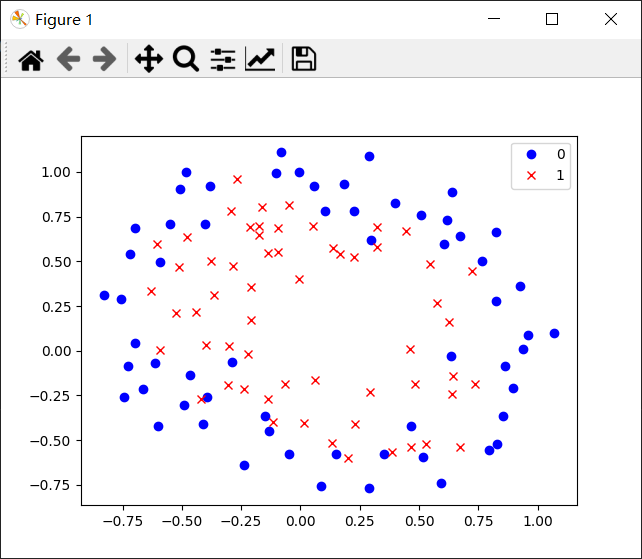
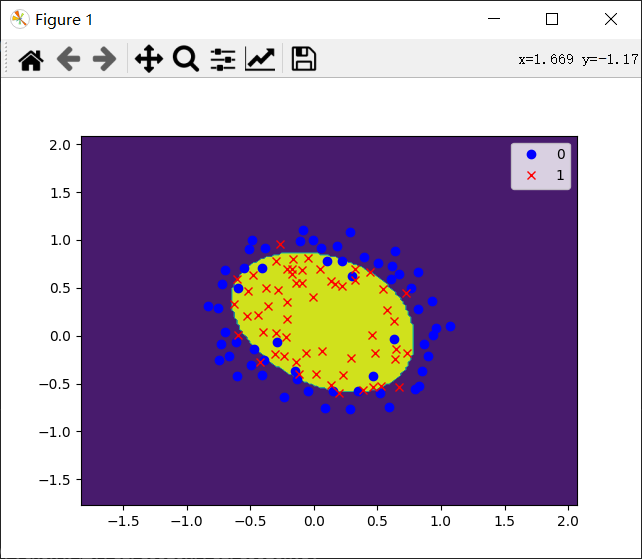
只是画图会有点困难，不太好画，只好做等高线图。

做等高线图之前，要把整个图的“高度”处理一下，所以又要用到之前用过的网格矩阵函数np.meshgrid()。然后，对于每个点，计算它的预测值，从而形成等高线图。这里的计算可以用快捷的矩阵乘法。

一些函数的含义与用法就放在参考博客里了。

Python代码如下：

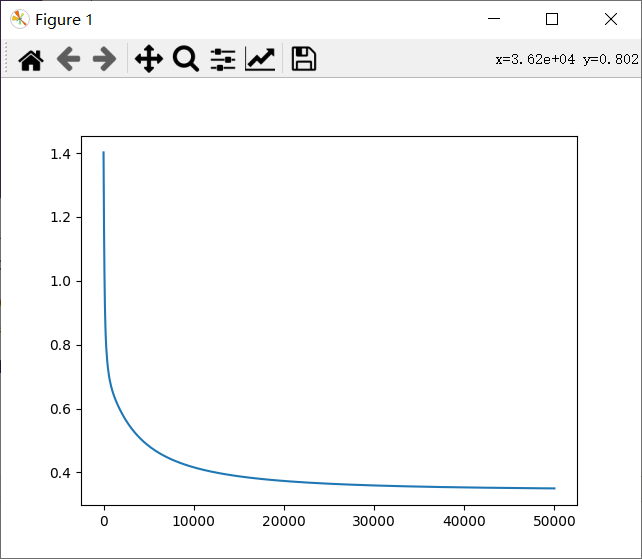
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report
from sklearn import preprocessing
from sklearn.preprocessing import PolynomialFeatures
#数据是否标准化
scale=False

#画图
def plot():
    p1,=plt.plot(x0,y0,'bo')
    p2,=plt.plot(x1,y1,'rx')
    plt.legend(handles=[p1,p2],labels=['0','1'],loc='best')

#sigmoid函数
def sig(x):
    return 1/(1+np.exp(-x))

#损失函数
def loss(x_mat,y_mat,w):
    left=np.multiply(y_mat,np.log(sig(x_mat*w)))
    right=np.multiply(1-y_mat,np.log(1-sig(x_mat*w)))
    return -np.sum(left+right)/float(len(y_mat))

data=np.genfromtxt('C:/Users/Lenovo/Desktop/学习/机器学习资料/逻辑回归/LR-testSet2.txt',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,-1,np.newaxis]
if scale: #数据标准化
    x_data=preprocessing.scale(x_data)
x0,y0,x1,y1=[],[],[],[]
for i in range(len(y_data)):
    if y_data[i]:
        x1.append(x_data[i,0])
        y1.append(x_data[i,1])
    else:
        x0.append(x_data[i,0])
        y0.append(x_data[i,1])
plot()
plt.show()

m,n=x_data.shape
model=PolynomialFeatures(degree=3) #最高次项为3次
X_data=model.fit_transform(x_data)
m,n=X_data.shape
lr=0.03
w=np.ones((n,1))
w=np.mat(w)
x_mat=np.mat(X_data)
y_mat=np.mat(y_data)
m=float(m)
costlist=[]
for i in range(50001):
    h=sig(x_mat*w)
    w_=x_mat.T*(h-y_mat)/m
    w-=lr*w_
    if i%50==0:
        costlist.append(loss(x_mat,y_mat,w)) #记录每次的Loss
print(w)

#画出决策边界
if scale==False:
    xmi=x_data[:,0].min()-1
    xma=x_data[:,0].max()+1
    ymi=x_data[:,1].min()-1
    yma=x_data[:,1].max()+1
    xx=np.arange(xmi,xma,0.02) #等差数列
    yy=np.arange(ymi,yma,0.02)
    xx,yy=np.meshgrid(xx,yy) #形成网格矩阵
    z=model.fit_transform(np.c_[xx.ravel(),yy.ravel()])*w #求出每个点对应的预测值
    for i in range(len(z)):
        if z[i]>0:
            z[i]=1
        else:
            z[i]=0
    z=z.reshape(xx.shape) #改变形状
    plot()
    plt.contourf(xx,yy,z) #作出等高线图
    plt.show()

predict=x_mat*w
for i in range(len(predict)):
    if predict[i]<=0:
        predict[i]=0
    else:
        predict[i]=1
print(classification_report(y_data,predict)) #正确率与召回率

#Loss值与梯度下降次数之间的关系
x=np.linspace(0,50000,1001)
plt.plot(x,costlist)
plt.show()

得到结果：

[[ 4.16787292]
[ 2.72213524]
[ 4.55120018]
[-9.76109006]
[-5.34880198]
[-8.51458023]
[-0.55950401]
[-1.55418165]
[-0.75929829]
[-2.88573877]]

　　　　　　precision　　recall　　f1-score　　support

0.0　　　　　　0.86　　　0.83　　　0.85　　　　60
1.0　　　　　　0.83　　　0.86　　　0.85　　　　58

accuracy　　　　　　　　　　　　　0.85　　　　118
macro avg　　　0.85　　　0.85　　　0.85　　　　118
weighted avg　　0.85　　　0.85　　　0.85　　　　118

参考博客：

python matplotlib contour画等高线图_Mr_Cat123的wudl博客-CSDN博客

Python Numpy模块函数np.c_和np.r_ - shaomine - 博客园 (cnblogs.com)

Python numpy中的ravel()，flatten()以及squeeze()的用法与区别_菜鸟小胡的学习空间-CSDN博客

使用数据：

0.051267,0.69956,1
-0.092742,0.68494,1
-0.21371,0.69225,1
-0.375,0.50219,1
-0.51325,0.46564,1
-0.52477,0.2098,1
-0.39804,0.034357,1
-0.30588,-0.19225,1
0.016705,-0.40424,1
0.13191,-0.51389,1
0.38537,-0.56506,1
0.52938,-0.5212,1
0.63882,-0.24342,1
0.73675,-0.18494,1
0.54666,0.48757,1
0.322,0.5826,1
0.16647,0.53874,1
-0.046659,0.81652,1
-0.17339,0.69956,1
-0.47869,0.63377,1
-0.60541,0.59722,1
-0.62846,0.33406,1
-0.59389,0.005117,1
-0.42108,-0.27266,1
-0.11578,-0.39693,1
0.20104,-0.60161,1
0.46601,-0.53582,1
0.67339,-0.53582,1
-0.13882,0.54605,1
-0.29435,0.77997,1
-0.26555,0.96272,1
-0.16187,0.8019,1
-0.17339,0.64839,1
-0.28283,0.47295,1
-0.36348,0.31213,1
-0.30012,0.027047,1
-0.23675,-0.21418,1
-0.06394,-0.18494,1
0.062788,-0.16301,1
0.22984,-0.41155,1
0.2932,-0.2288,1
0.48329,-0.18494,1
0.64459,-0.14108,1
0.46025,0.012427,1
0.6273,0.15863,1
0.57546,0.26827,1
0.72523,0.44371,1
0.22408,0.52412,1
0.44297,0.67032,1
0.322,0.69225,1
0.13767,0.57529,1
-0.0063364,0.39985,1
-0.092742,0.55336,1
-0.20795,0.35599,1
-0.20795,0.17325,1
-0.43836,0.21711,1
-0.21947,-0.016813,1
-0.13882,-0.27266,1
0.18376,0.93348,0
0.22408,0.77997,0
0.29896,0.61915,0
0.50634,0.75804,0
0.61578,0.7288,0
0.60426,0.59722,0
0.76555,0.50219,0
0.92684,0.3633,0
0.82316,0.27558,0
0.96141,0.085526,0
0.93836,0.012427,0
0.86348,-0.082602,0
0.89804,-0.20687,0
0.85196,-0.36769,0
0.82892,-0.5212,0
0.79435,-0.55775,0
0.59274,-0.7405,0
0.51786,-0.5943,0
0.46601,-0.41886,0
0.35081,-0.57968,0
0.28744,-0.76974,0
0.085829,-0.75512,0
0.14919,-0.57968,0
-0.13306,-0.4481,0
-0.40956,-0.41155,0
-0.39228,-0.25804,0
-0.74366,-0.25804,0
-0.69758,0.041667,0
-0.75518,0.2902,0
-0.69758,0.68494,0
-0.4038,0.70687,0
-0.38076,0.91886,0
-0.50749,0.90424,0
-0.54781,0.70687,0
0.10311,0.77997,0
0.057028,0.91886,0
-0.10426,0.99196,0
-0.081221,1.1089,0
0.28744,1.087,0
0.39689,0.82383,0
0.63882,0.88962,0
0.82316,0.66301,0
0.67339,0.64108,0
1.0709,0.10015,0
-0.046659,-0.57968,0
-0.23675,-0.63816,0
-0.15035,-0.36769,0
-0.49021,-0.3019,0
-0.46717,-0.13377,0
-0.28859,-0.060673,0
-0.61118,-0.067982,0
-0.66302,-0.21418,0
-0.59965,-0.41886,0
-0.72638,-0.082602,0
-0.83007,0.31213,0
-0.72062,0.53874,0
-0.59389,0.49488,0
-0.48445,0.99927,0
-0.0063364,0.99927,0
0.63265,-0.030612,0