机器学习笔记（十一）——线性逻辑回归（梯度下降法）

本博客仅用于个人学习，不用于传播教学，主要是记自己能够看得懂的笔记（

学习知识、资源和数据来自：机器学习算法基础-覃秉丰_哔哩哔哩_bilibili

这次bb多一点呗。逻辑回归有点离谱。

逻辑回归最重要的就是一个分类函数：

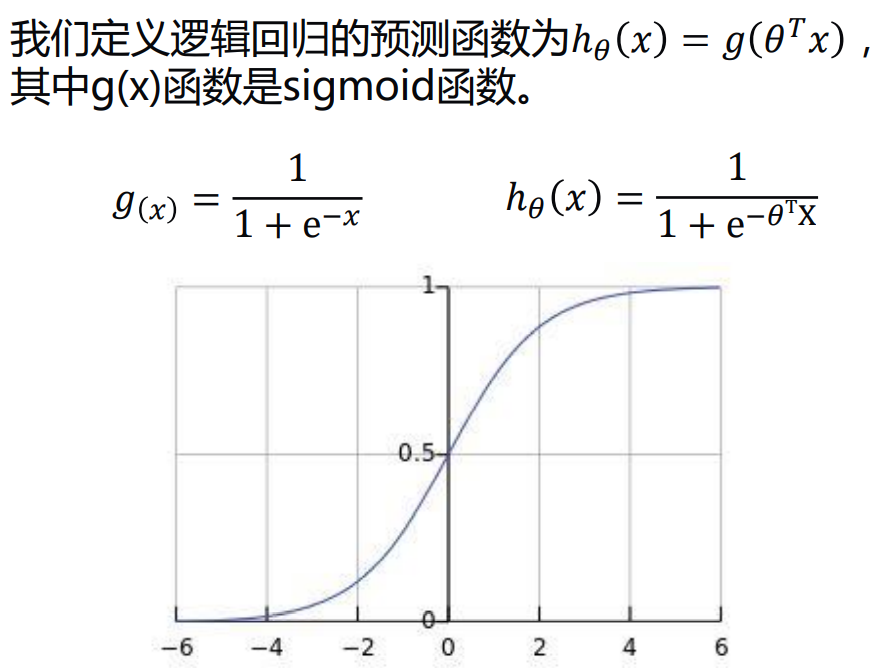
我们可以把大于0.5的部分称为1类，小于0.5的部分称为0类。其实这两类也就是θT*X大于0还是小于0的问题。（X*θ=X*w=θT*X）（后面加T表转置）

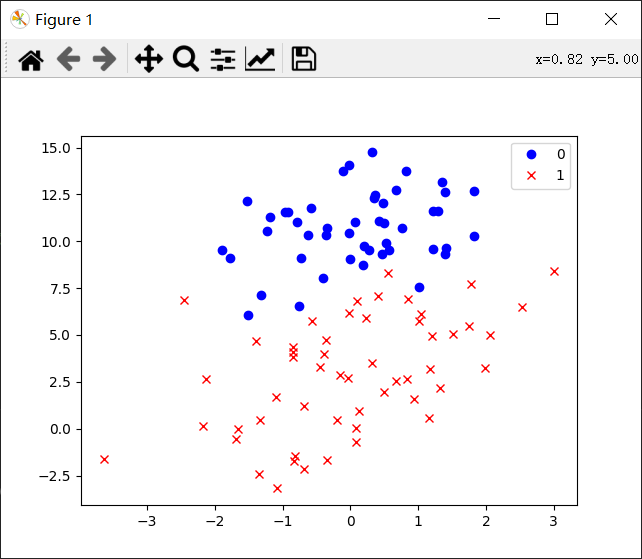
X*w与0的关系，其实就是一张图上的点和X*w所表示的线之间的关系。如下图：

所以，关键就是找出决策边界，求出决策边界的表达式。这里可以用与线性回归一样的梯度下降法。所用的Loss函数如下：

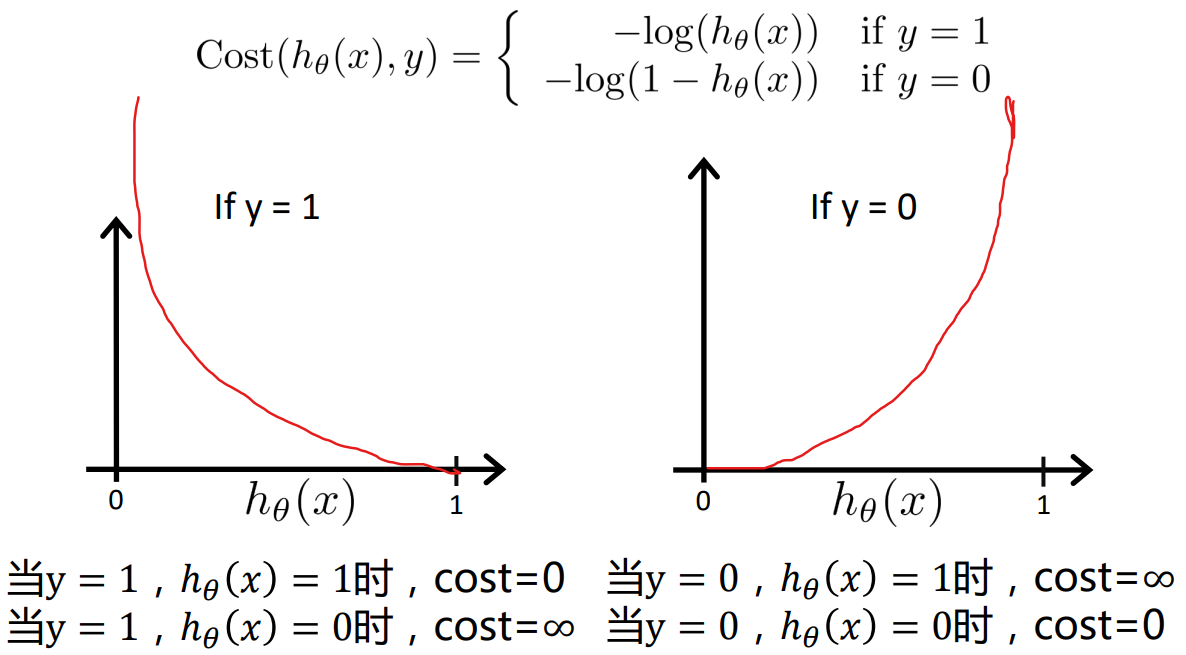
可以写成：

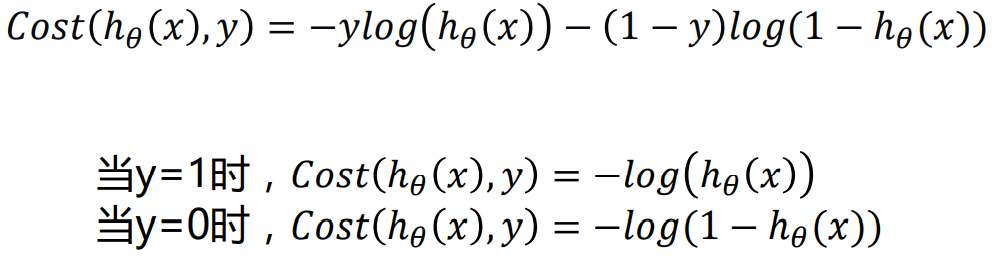
对其求导得：

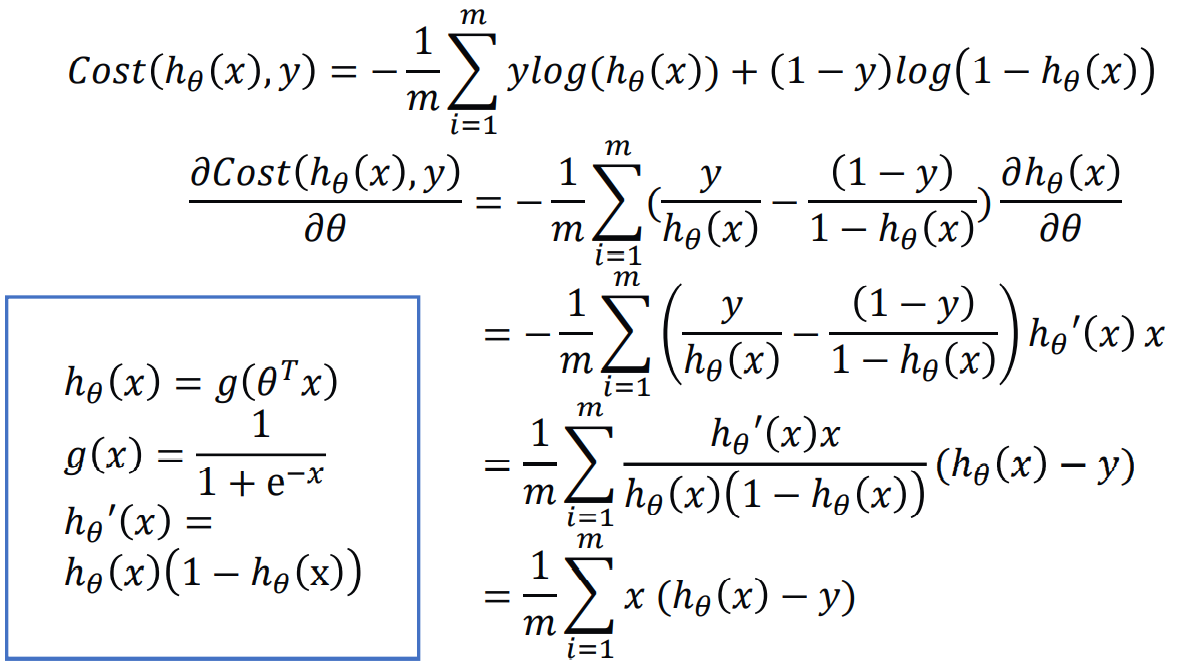
最后的结果用矩阵可表示为XT*(sigmoid(X*w)-Y)/m。

所以可以写出以下代码：（注：代码中是否标准化可以自己调）

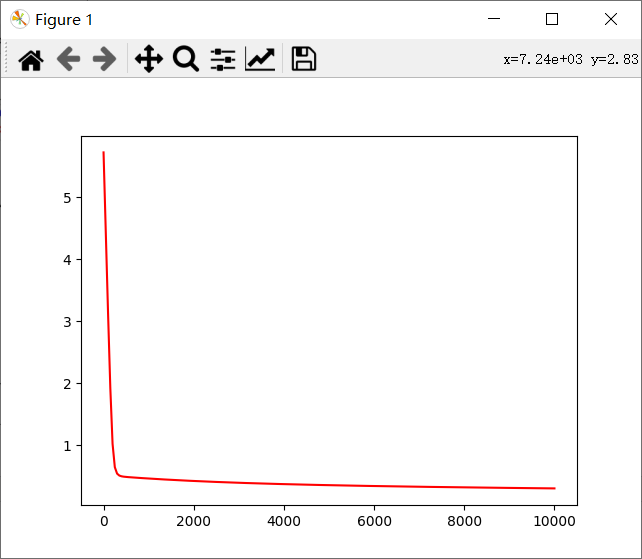
import numpy as np
from sklearn import preprocessing
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
#数据是否标准化
scale=False

#sigmoid函数
def sig(x):
    return 1/(1+np.exp(-x))

#逻辑回归中的损失函数
def loss(x_mat,y_mat,w):
    left=np.multiply(y_mat,np.log(sig(x_mat*w)))
    right=np.multiply(1-y_mat,np.log(1-sig(x_mat*w)))
    return np.sum(left+right)/float(-(len(x_mat)))

#画散点图
def plot():
    p1,=plt.plot(x0,y0,'bo',label='0')
    p2,=plt.plot(x1,y1,'rx',label='1')
    plt.legend(handles=[p1,p2],loc='best') #画出图例

data=np.genfromtxt('C:/Users/Lenovo/Desktop/学习/机器学习资料/逻辑回归/LR-testSet.csv',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,-1,np.newaxis]
if scale:
    preprocessing.scale(x_data) #数据标准化
x0,y0,x1,y1=[],[],[],[]
for i in range(len(y_data)): #分类
    if y_data[i]==0:
        x0.append(x_data[i,0])
        y0.append(x_data[i,1])
    else:
        x1.append(x_data[i,0])
        y1.append(x_data[i,1])

plot()
plt.show()

X_data=np.concatenate((np.ones((100,1)),x_data),axis=1)

x_mat=np.mat(X_data)
y_mat=np.mat(y_data)
lr=0.001
m,n=x_mat.shape
m=float(m)
w=np.mat(np.ones((n,1)))
costlist=[]
for i in range(10001): #梯度下降10001次
    h=sig(x_mat*w)
    w_=x_mat.T*(h-y_mat)/m #得到求导后的向量
    '''
    if i==0:
        print(h)
        print(w_)
    '''
    w=w-lr*w_
    if i%50==0:
        costlist.append(loss(x_mat,y_mat,w)) #每50次记录一次Loss值

#结果输出
print(w)

#画出决策边界的图
if scale==False: #数据标准化后再画此图没有意义
    plot()
    w=np.array(w)
    plt.plot(x_data[:,0],(-w[0]-x_data[:,0]*w[1])/w[2],'k')
    plt.show()

#画出Loss随下降次数的变化
x=np.linspace(0,10000,201)
plt.plot(x,costlist,'r')
plt.show()

#利用sklearn自带的函数求真实值与预测值的区别，输出正确率和召回率
predict=[1 if x>=0.5 else 0 for x in sig(x_mat*w)]
print(classification_report(y_data,predict))

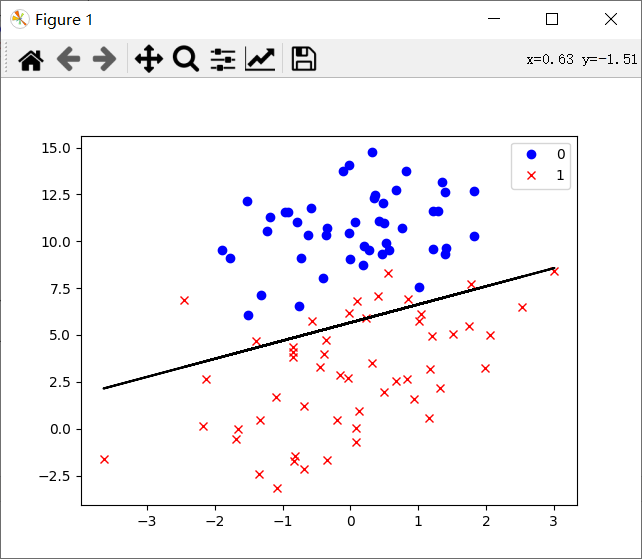
得到结果：

[[ 2.05836354]
[ 0.3510579 ]
[-0.36341304]]

　　　　precision　　recall　　f1-score　　support

　　0.0　　0.82　　　1.00　　　0.90　　　　47
　　1.0　　1.00　　　0.81　　　0.90　　　　53

accuracy 　　　　　　　　　　　0.90　　　　100
macro avg   0.91　　　0.91　　　0.90　　　　100
weighted avg 0.92　　 0.90　　　0.90　　　　100

关于正确率和召回率：见B站教学视频。

参考博客：

matplotlib命令与格式：图例legend语法及设置_开码河粉-CSDN博客

机器学习笔记－－classification_report&精确度/召回率/F1值_akadiao的博客-CSDN博客

交叉熵_听话的耳背少年的博客-CSDN博客

图片来源：

上方B站链接里的PPT。

使用数据：

-0.017612,14.053064,0
-1.395634,4.662541,1
-0.752157,6.53862,0
-1.322371,7.152853,0
0.423363,11.054677,0
0.406704,7.067335,1
0.667394,12.741452,0
-2.46015,6.866805,1
0.569411,9.548755,0
-0.026632,10.427743,0
0.850433,6.920334,1
1.347183,13.1755,0
1.176813,3.16702,1
-1.781871,9.097953,0
-0.566606,5.749003,1
0.931635,1.589505,1
-0.024205,6.151823,1
-0.036453,2.690988,1
-0.196949,0.444165,1
1.014459,5.754399,1
1.985298,3.230619,1
-1.693453,-0.55754,1
-0.576525,11.778922,0
-0.346811,-1.67873,1
-2.124484,2.672471,1
1.217916,9.597015,0
-0.733928,9.098687,0
-3.642001,-1.618087,1
0.315985,3.523953,1
1.416614,9.619232,0
-0.386323,3.989286,1
0.556921,8.294984,1
1.224863,11.58736,0
-1.347803,-2.406051,1
1.196604,4.951851,1
0.275221,9.543647,0
0.470575,9.332488,0
-1.889567,9.542662,0
-1.527893,12.150579,0
-1.185247,11.309318,0
-0.445678,3.297303,1
1.042222,6.105155,1
-0.618787,10.320986,0
1.152083,0.548467,1
0.828534,2.676045,1
-1.237728,10.549033,0
-0.683565,-2.166125,1
0.229456,5.921938,1
-0.959885,11.555336,0
0.492911,10.993324,0
0.184992,8.721488,0
-0.355715,10.325976,0
-0.397822,8.058397,0
0.824839,13.730343,0
1.507278,5.027866,1
0.099671,6.835839,1
-0.344008,10.717485,0
1.785928,7.718645,1
-0.918801,11.560217,0
-0.364009,4.7473,1
-0.841722,4.119083,1
0.490426,1.960539,1
-0.007194,9.075792,0
0.356107,12.447863,0
0.342578,12.281162,0
-0.810823,-1.466018,1
2.530777,6.476801,1
1.296683,11.607559,0
0.475487,12.040035,0
-0.783277,11.009725,0
0.074798,11.02365,0
-1.337472,0.468339,1
-0.102781,13.763651,0
-0.147324,2.874846,1
0.518389,9.887035,0
1.015399,7.571882,0
-1.658086,-0.027255,1
1.319944,2.171228,1
2.056216,5.019981,1
-0.851633,4.375691,1
-1.510047,6.061992,0
-1.076637,-3.181888,1
1.821096,10.28399,0
3.01015,8.401766,1
-1.099458,1.688274,1
-0.834872,-1.733869,1
-0.846637,3.849075,1
1.400102,12.628781,0
1.752842,5.468166,1
0.078557,0.059736,1
0.089392,-0.7153,1
1.825662,12.693808,0
0.197445,9.744638,0
0.126117,0.922311,1
-0.679797,1.22053,1
0.677983,2.556666,1
0.761349,10.693862,0
-2.168791,0.143632,1
1.38861,9.341997,0
0.317029,14.739025,0