机器学习笔记(六)——线性回归标准方程法
本博客仅用于个人学习,不用于传播教学,主要是记自己能够看得懂的笔记(
学习知识、资源和数据来自:机器学习算法基础-覃秉丰_哔哩哔哩_bilibili
关于线性回归的标准方程法,原理推导与矩阵微积分有关,我也没学过,毕竟我线性代数是比较差,想深挖的看上面的视频或者去看其他博客吧。根据公式以及推导,可得
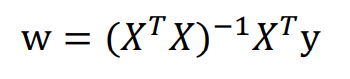
其中w为权值列向量,X为x系数矩阵,y为y系数列向量。下图或许更直观:
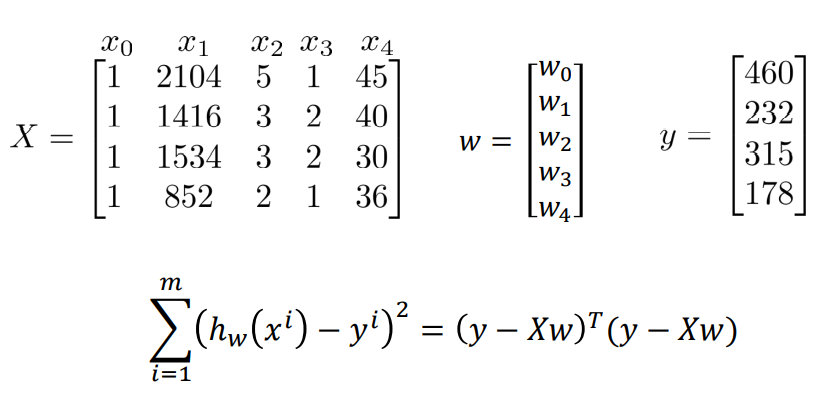
基本了解了原理后,我们可以直接通过公式,算出w向量,从而求得参数。
对于机器学习笔记(一)——一元线性回归(梯度下降法) - Lcy的瞎bb - 博客园 (cnblogs.com)中的问题,可以有以下解法:
import numpy as np import matplotlib.pyplot as plt import sys data=np.genfromtxt('C:/Users/Lenovo/Desktop/学习/机器学习资料/线性回归以及非线性回归/data.csv',delimiter=',') x_data=data[:,0,np.newaxis] y_data=data[:,1,np.newaxis] X_data=np.concatenate((np.ones([100,1]),x_data),axis=1) #为x_data添加一列1,作为x0,也就是常数项 x_mat=np.mat(X_data) y_mat=np.mat(y_data) xtx=x_mat.T*x_mat if np.linalg.det(xtx)==0.0: #判断xT*x是不是可逆矩阵 print("This matrix can not do inverse.") sys.exit() w=xtx.I*x_mat.T*y_mat #标准方程法:w=(xT*x)^(-1)*xT*y,代码中xtx.I即为xT*x的逆矩阵 z=x_mat*w #矩阵乘法求预测值 plt.plot(x_data,y_data,'b.') plt.plot(x_data,z,'r') plt.show()
得到结果:
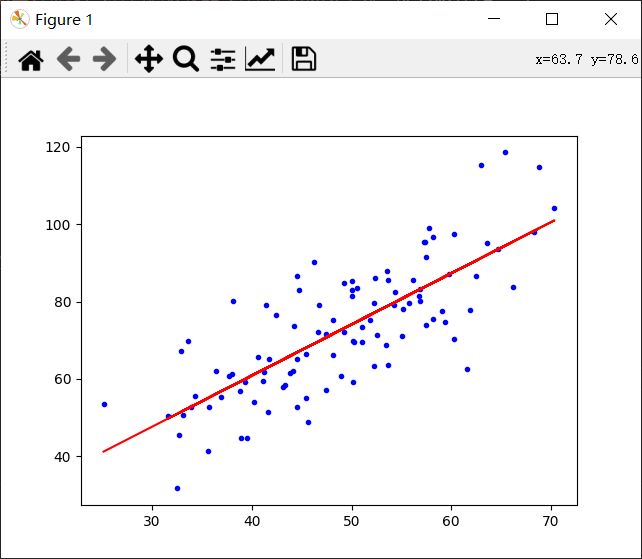
这是一元的例子。
对于机器学习笔记(三)——多元线性回归(梯度下降法) - Lcy的瞎bb - 博客园 (cnblogs.com)中的多元问题,代码如下:
import numpy as np import matplotlib.pyplot as plt import sys from mpl_toolkits.mplot3d import Axes3D data=np.genfromtxt('C:/Users/Lenovo/Desktop/学习/机器学习资料/线性回归以及非线性回归/Delivery.csv',delimiter=',') x_data=data[:,:-1] y_data=data[:,-1,np.newaxis] X_data=np.concatenate((np.ones([10,1]),x_data),axis=1) #为x_data添加一列1,作为x0,也就是常数项 x_mat=np.mat(X_data) y_mat=np.mat(y_data) xtx=x_mat.T*x_mat if np.linalg.det(xtx)==0.0: #判断xT*x是不是可逆矩阵 print("This matrix can not do inverse.") sys.exit() w=xtx.I*x_mat.T*y_mat #标准方程法:w=(xT*x)^(-1)*xT*y,代码中xtx.I即为xT*x的逆矩阵 w=np.array(w) #将w向量转化为数组 #画3D图 fig=plt.figure() ax=fig.add_subplot(111,projection='3d') ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o',s=100) x1=x_data[:,0] x2=x_data[:,1] x1,x2=np.meshgrid(x1,x2) z=w[0]+w[1]*x1+w[2]*x2 ax.plot_surface(x1,x2,z) plt.show()
得到结果:
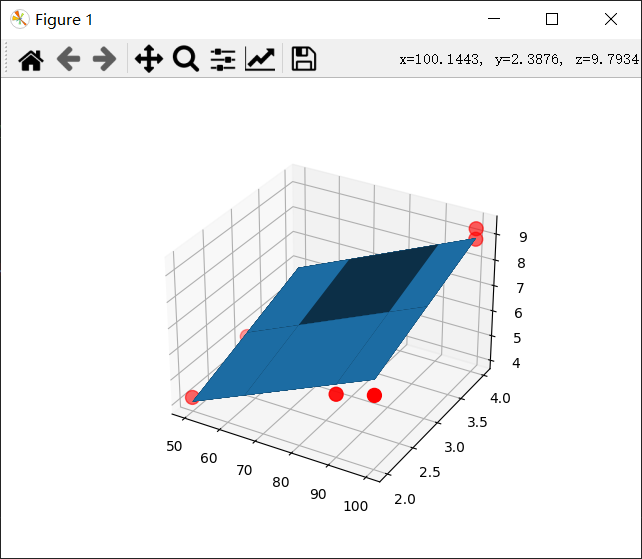
参考博客:




