机器学习笔记（三）——多元线性回归（梯度下降法）

本博客仅用于个人学习，不用于传播教学，主要是记自己能够看得懂的笔记（

因为自己基础不厚，对Python的运用不太熟，因此在画3D图的时候有亿点点问题。相关博客我会在底下列出。所用数据也会在底下列出，可自己保存为csv文件。

多元线性回归的梯度下降法与一元线性回归没有什么特别大的差别，只是多了点x参数而已。原理就不多说了，直接上代码：

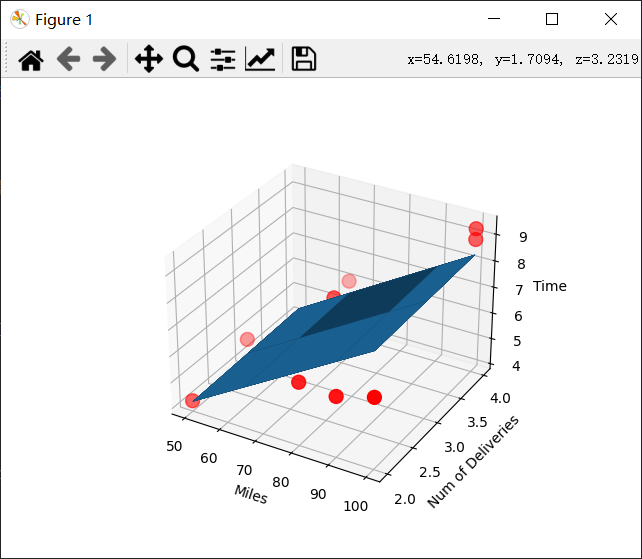
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Loss函数
def cal_error(a,b,c,x_data,y_data):
    sum=0
    for i in range(len(y_data)):
        sum+=(a+b*x_data[i,0]+c*x_data[i,1]-y_data[i])**2
    return sum/float(len(y_data))/2.0

#载入数据
data=np.genfromtxt('C:/Users/Lenovo/Desktop/学习/机器学习资料/线性回归以及非线性回归/Delivery.csv',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,-1]
a,b,c=0,0,0
m=float(len(y_data))
lr=0.0001
print("a={0},b={1},c={2},error={3}".format(a,b,c,cal_error(a,b,c,x_data,y_data)))

#梯度下降法
for i in range(1000): #梯度下降1000次
    a_,b_,c_=0,0,0
    for j in range(len(y_data)):
        a_+=(1/m)*(a+b*x_data[j,0]+c*x_data[j,1]-y_data[j])
        b_+=(1/m)*x_data[j,0]*(a+b*x_data[j,0]+c*x_data[j,1]-y_data[j])
        c_+=(1/m)*x_data[j,1]*(a+b*x_data[j,0]+c*x_data[j,1]-y_data[j])
    a-=lr*a_
    b-=lr*b_
    c-=lr*c_

#输出结果
print("a={0},b={1},c={2},error={3}".format(a,b,c,cal_error(a,b,c,x_data,y_data))) #输出
#3D画图
fig=plt.figure() #创建一个图
ax=fig.add_subplot(111,projection='3d') #创建一个3D图
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o',s=100) #绘制3D散点图
x0=x_data[:,0]
x1=x_data[:,1]
x0,x1=np.meshgrid(x0,x1) #生成网格点坐标矩阵
z=a+b*x0+c*x1
ax.plot_surface(x0,x1,z)
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')

plt.show()