机器学习笔记（一）——一元线性回归（梯度下降法）

因为是个人学习笔记向（主要是懒，啥也不想写），所以就不仔细介绍一元线性回归以及梯度下降法的具体概念了，相关知识可参见高中数学课本（一元线性回归部分）和其他博客（梯度下降法），本文只注重梯度下降法的Python实现。

学习知识、资源与数据来源：机器学习算法基础-覃秉丰_哔哩哔哩_bilibili

使用的数据在最下方，可自己保存成csv文件。

Python代码如下：

import numpy as np
import matplotlib.pyplot as plt

#计算损失函数（loss函数）
def cal_error(b,k,x_data,y_data):
    sum=0
    for i in range(len(x_data)):
        sum+=(y_data[i]-(k*x_data[i]+b))**2
    return sum/float(len(x_data))/2.0 #L(b,k)=i从0到len(x_data)对(y_data[i]-(k*x_data[i]+b))**2求和÷len(x_data)再÷2（因为求导时不用再乘2）

#导入文件里的数据，数据第一列为x，第二列为y
data=np.genfromtxt('C:/Users/Lenovo/Desktop/线性回归以及非线性回归/data.csv',delimiter=',')
x_data=data[:,0]
y_data=data[:,1]
b=0 #截距
k=0 #斜率
lr=0.0001 #梯度下降法中的learning rate
m=float(len(x_data))

for i in range(50): #梯度下降50次
    b_,k_=0.0,0.0 #loss函数关于b和k的偏导
    for j in range(len(x_data)):
        b_+=-(1/m)*(y_data[j]-(k*x_data[j]+b))
        k_+=-(1/m)*x_data[j]*(y_data[j]-(k*x_data[j]+b))
    b-=lr*b_ #梯度下降法
    k-=lr*k_

print("b={0},k={1},error={2}".format(b,k,cal_error(b, k, x_data, y_data)))
#画图
plt.plot(x_data,y_data,'b.')
plt.plot(x_data,k*x_data+b,'r')
plt.show()

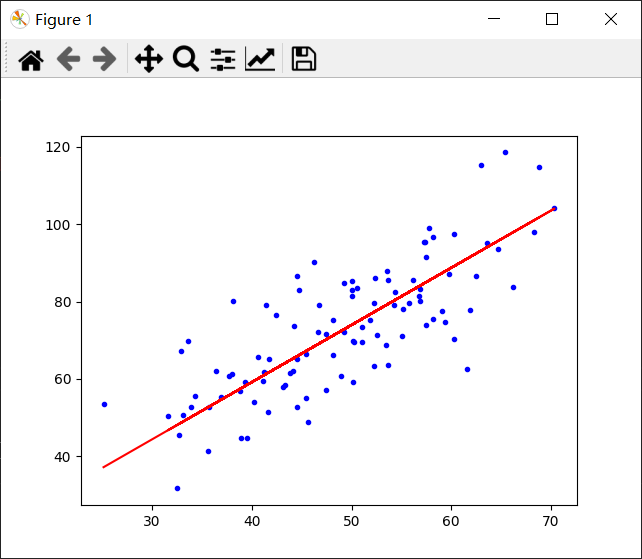
最后的结果：

b=0.030569950649287983,k=1.4788903781318357,error=56.32488184238028

使用的数据：

32.502345269453031,31.70700584656992
53.426804033275019,68.77759598163891
61.530358025636438,62.562382297945803
47.475639634786098,71.546632233567777
59.813207869512318,87.230925133687393
55.142188413943821,78.211518270799232
52.211796692214001,79.64197304980874
39.299566694317065,59.171489321869508
48.10504169176825,75.331242297063056
52.550014442733818,71.300879886850353
45.419730144973755,55.165677145959123
54.351634881228918,82.478846757497919
44.164049496773352,62.008923245725825
58.16847071685779,75.392870425994957
56.727208057096611,81.43619215887864
48.955888566093719,60.723602440673965
44.687196231480904,82.892503731453715
60.297326851333466,97.379896862166078
45.618643772955828,48.847153317355072
38.816817537445637,56.877213186268506
66.189816606752601,83.878564664602763
65.41605174513407,118.59121730252249
47.48120860786787,57.251819462268969
41.57564261748702,51.391744079832307
51.84518690563943,75.380651665312357
59.370822011089523,74.765564032151374
57.31000343834809,95.455052922574737
63.615561251453308,95.229366017555307
46.737619407976972,79.052406169565586
50.556760148547767,83.432071421323712
52.223996085553047,63.358790317497878
35.567830047746632,41.412885303700563
42.436476944055642,76.617341280074044
58.16454011019286,96.769566426108199
57.504447615341789,74.084130116602523
45.440530725319981,66.588144414228594
61.89622268029126,77.768482417793024
33.093831736163963,50.719588912312084
36.436009511386871,62.124570818071781
37.675654860850742,60.810246649902211
44.555608383275356,52.682983366387781
43.318282631865721,58.569824717692867
50.073145632289034,82.905981485070512
43.870612645218372,61.424709804339123
62.997480747553091,115.24415280079529
32.669043763467187,45.570588823376085
40.166899008703702,54.084054796223612
53.575077531673656,87.994452758110413
33.864214971778239,52.725494375900425
64.707138666121296,93.576118692658241
38.119824026822805,80.166275447370964
44.502538064645101,65.101711570560326
40.599538384552318,65.562301260400375
41.720676356341293,65.280886920822823
51.088634678336796,73.434641546324301
55.078095904923202,71.13972785861894
41.377726534895203,79.102829683549857
62.494697427269791,86.520538440347153
49.203887540826003,84.742697807826218
41.102685187349664,59.358850248624933
41.182016105169822,61.684037524833627
50.186389494880601,69.847604158249183
52.378446219236217,86.098291205774103
50.135485486286122,59.108839267699643
33.644706006191782,69.89968164362763
39.557901222906828,44.862490711164398
56.130388816875467,85.498067778840223
57.362052133238237,95.536686846467219
60.269214393997906,70.251934419771587
35.678093889410732,52.721734964774988
31.588116998132829,50.392670135079896
53.66093226167304,63.642398775657753
46.682228649471917,72.247251068662365
43.107820219102464,57.812512976181402
70.34607561504933,104.25710158543822
44.492855880854073,86.642020318822006
57.50453330326841,91.486778000110135
36.930076609191808,55.231660886212836
55.805733357942742,79.550436678507609
38.954769073377065,44.847124242467601
56.901214702247074,80.207523139682763
56.868900661384046,83.14274979204346
34.33312470421609,55.723489260543914
59.04974121466681,77.634182511677864
57.788223993230673,99.051414841748269
54.282328705967409,79.120646274680027
51.088719898979143,69.588897851118475
50.282836348230731,69.510503311494389
44.211741752090113,73.687564318317285
38.005488008060688,61.366904537240131
32.940479942618296,67.170655768995118
53.691639571070056,85.668203145001542
68.76573426962166,114.85387123391394
46.230966498310252,90.123572069967423
68.319360818255362,97.919821035242848
50.030174340312143,81.536990783015028
49.239765342753763,72.111832469615663
50.039575939875988,85.232007342325673
48.149858891028863,66.224957888054632
25.128484647772304,53.454394214850524