「FHQ_Treap」学习笔记
一、前言 & 基本理论
来自笔者的肯定:最容易理解且比较好写的平衡树(不过就是常数有点大了),可能是笔者花了较长的时间去理解旋转 Treap 和 Splay 的旋转吧()。
FHQ 不仅比旋转法编码简单,而且能用于区间翻转、移动、持久化等场合。——《算法竞赛》
FHQ_Treap 的所有操作都只用到了分裂和合并这两个基本操作,这两个操作的复杂度都为 \(O(\log n)\)。
二、定义
定义结构体 FHQ_Treap:
struct FHQ_Treap
{
int ls,rs;
int val,pri;
int siz;
}t[N];
ls,rs,左儿子 / 右儿子。val,键值(权值)。pri,随机的优先级,搭配srand(time(0));食用。siz,当前节点为根的子树的节点数量,用于求第 \(k\) 大和排名。
全文的宏定义如下:
#define ls(u) t[u].ls//左儿子
#define rs(u) t[u].rs//右儿子
三、分裂和合并的代码实现
写在前面:
update操作:
void update(int u)//更新以 u 为根的子树的 siz
{
t[u].siz=t[ls(u)].siz+t[rs(u)].siz+1;
}
- 本小节所有的代码都没有引用
push_down函数,再后面几小节会出现其代码(其实和线段树懒标记一个东西)。
详见 5.2节 区间翻转。
3.1 分裂操作
void split(int u,int x,int &L,int &R),其中 &L 和 &R 是引用传递,函数返回 \(L\) 和 \(R\) 的值。
- 权值分裂
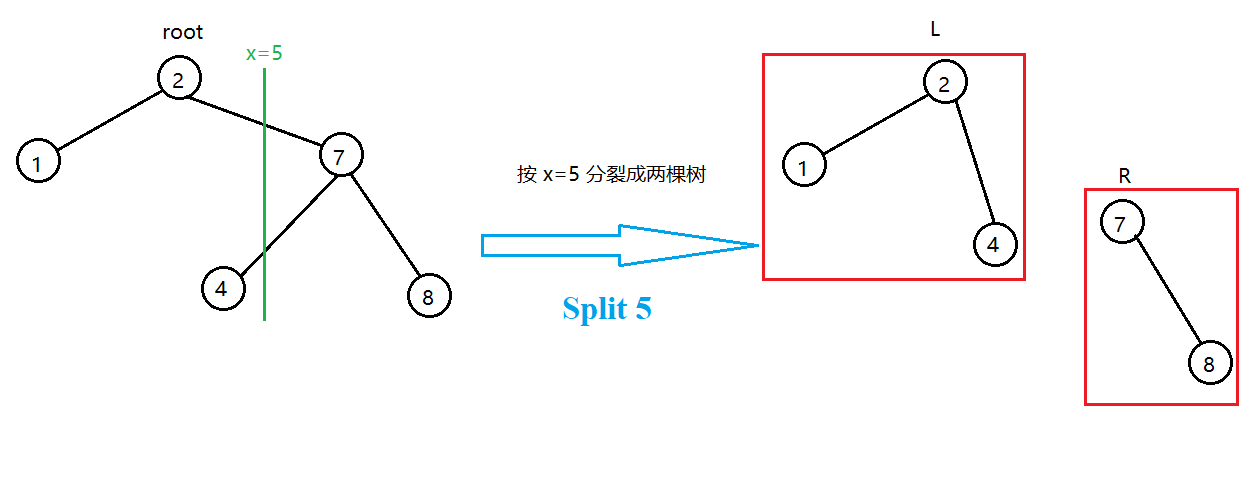
分裂后,左子树上所有的节点的键值 \(val\) 都小于右树。
即左树 \(L\) 上所有的节点的键值都小于或等于 \(x\),右树 \(R\) 上所有节点的键值都大于 \(x\)。
void split(int u,int x,int &L,int &R)//权值分裂,返回以 L 和 R 为根的两棵树
{
if(!u)//0 表示没有孩子,到达叶子,递归返回
{
L=R=0;
return;
}
if(t[u].val<=x)//本节点的键值比 x 小,那么到右子树上找 x
{
L=u;//左树的根是本节点
split(rs(u),x,rs(u),R);//通过 rs 传回新的子节点
}
else//本节点比 x 大,继续到左子树上找 x
{
R=u;//右树的根是本节点
split(ls(u),x,L,ls(u));
}
update(u);//更新当前节点的 siz
}
- 排名分裂
把树 \(u\) 分裂成包含前 \(x\) 个数的 \(L\) 和包含其他数的 \(R\)。
void split(int u,int x,int &L,int &R)//排名分裂
{
if(!u)
{
L=R=0;
return;
}
if(t[ls(u)].siz+1<=x)//第 x 个数在 u 的右子树上
{
L=u;
spilt(t[L].rs,x-t[ls(u)].siz-1,t[L].rs,R);
}
else//第 x 个数在左子树上
{
R=u;
split(t[R].ls,x,L,t[R].ls);
}
update(u);
}
3.2 合并操作
int merge(int L,int R),合并树 \(L\) 和 \(R\)。因为有 \(L\) 上所有节点的键值 \(val\) 都小于 \(R\) 的节点的隐含条件,所以合并时只需考虑节点的优先级 \(pri\)。
显然,新树的根是 \(L\) 和 \(R\) 中优先级最大的那个。
int merge(int L,int R)//合并以 L 和 R 为根的两棵树,返回一棵树的根
{
if(!L||!R) return L+R;//到达叶子,如 L==0 就是返回 L+R=R
if(t[L].pri>t[R].pri)//左树 L 优先级大于右树 R,则 L 节点是父节点
{
t[L].rs=merge(t[L].rs,R);//合并 R 和 L 的右儿子,并更新 L 的右儿子
update(L);
return L;//合并后的根是 L
}
else//合并后 R 是父节点
{
t[R].ls=merge(L,t[R].ls);//合并 L 和 R 的左儿子,并更新 R 的左儿子
update(R);
return R;//合并后的根是 R
}
}
其实,由于这里的优先级 \(phi\) 是随机生成的,尽可能的使树的结构趋向于平均,其实在一些空间卡得比较死的题可以不用定义 \(phi\),用以下代码来实现合并的优先级:
int merge(int L,int R)
{
if(!L||!R) return L|R;
if(rand()%(t[L].siz+t[R].siz)<t[L].siz)
{
L=clone(L);
t[L].rs=merge(t[L].rs,R);
update(L);
return L;
}
else
{
t[R].ls=merge(L,t[R].ls);
update(R);
return R;
}
}
四、其他操作的代码实现
4.1 插入节点
int newNode(int x),新建节点和 void insert(int x),插入节点,按新节点 \(x\) 的键值把树分裂成 \(L\) 和 \(R\) 两棵树,新建节点 \(x\),合并 \(L\) 和 \(x\),再继续与 \(R\) 合并。
int newNode(int x)//建立只有一个点的树
{
int u=++cnt;
t[u].ls=t[u].rs=0;//0 表示没有子节点
t[u].val=x;
t[u].pri=rand();
t[u].siz=1;
return u;
}
void insert(int x)//插入数字 x
{
int L,R;
split(root,x,L,R);
root=merge(merge(L,newNode(x)),R);
}
4.2 删除节点
写在前面:
下文所提到的删除节点写的模板是针对删除 \(1\) 个数的,如果要删除区间 \([x,y]\) 只需将第一个 split 的 \(x\) 改成 \(y\) 即可。
- 权值分裂删除
void del(int x),把树 \(u\) 按 \(x\) 分裂为根小于或等于 \(x\) 的树 \(L\) 和大于 \(x\) 的树 \(R\),再把 \(L\) 分裂为根小于 \(x\) 的树 \(L\) 和根等于 \(x\) 的树 \(p\),合并 \(p\) 的左右儿子,即删除了 \(x\),最后合并 \(L,p,R\)(这里是指删除一个 \(x=p\) 的数,若要全部删除就无须合并 \(x=p\) 的左右子树)。
void del(int x)
{
int L,R,p;
split(root,x,L,R);//<=x 的树和 >x 的树
split(L,x-1,L,p);//<x 的树和 >=x 的树
p=merge(t[p].ls,t[p].rs);//合并 x=p 的左右子树,即删除了 x
root=merge(merge(L,p),R);
}
- 排名分裂删除
void del(int x),把树 \(u\) 分裂成包含前 \(x\) 个树的 \(L\) 和包含其他数的 \(R\),不需要合并 \(p\) 的左右子树。
void del(int x)
{
int L,R,p;
split(root,x,L,R);
split(L,x-1,L,p);
root=merge(L,R);
}
4.3 排名
int rnk(int x),求数字 \(x\) 的排名,把树 \(u\) 按 \(x-1\) 分裂成 \(L\) 和 \(R\),\(L\) 中包含了所有小于 \(x\) 的树,那么 \(x\) 的排名为 \(siz_L+1\),排名之后记得合并 \(L\) 和 \(R\) 恢复成原来的树。
int rnk(int x)//查询 x 的排名
{
int L,R;
split(root,x-1,L,R);//<x 的树和 >=x 的树
int ans=t[L].siz+1;
root=merge(L,R);//恢复
return ans;
}
4.4 求第 \(k\) 大数
int kth(int u,int k),根据节点的 \(siz\) 值不断递归整棵树,求得第 \(k\) 大数。
int kth(int u,int k)//求排名第 k 的数
{
if(k==t[ls(u)].siz+1) return u;//这个数为根
if(k<=t[ls(u)].siz) return kth(ls(u),k);//在左子树
if(k>t[ls(u)].siz) return kth(rs(u),k-t[ls(u)].siz-1);//在右子树
}
主函数记得写的是 t[kth(root,k)].val。
4.5 前驱
int pre(int x),求比 \(x\) 小的数。把树 \(u\) 分裂成 \(L\) 和 \(R\),在 \(L\) 中找最大的树(利用求第 \(k\) 大的操作)。找到后,合并 \(L\) 和 \(R\) 恢复成原来的树。
int pre(int x)//求 x 的前驱
{
int L,R;
split(root,x-1,L,R);
int ans=t[kth(L,t[L].siz)].val;
root=merge(L,R);//恢复
return ans;
}
4.6 后继
int nxt(int x),求比 \(x\) 大的数。把树 \(u\) 分裂成 \(L\) 和 \(R\),在 \(R\) 中找最小的树(利用求第 \(k\) 大的操作)。找到后,合并 \(L\) 和 \(R\) 恢复成原来的树。
int nxt(int x)//求 x 的后继
{
int L,R;
split(root,x,L,R);
int ans=t[kth(R,1)].val;
root=merge(L,R);//恢复
return ans;
}
讲完这里其实已经讲完一道例题了()
例1. P3369 【模板】普通平衡树
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入一个数 \(x\)。
- 删除一个数 \(x\)(若有多个相同的数,应只删除一个)。
- 定义排名为比当前数小的数的个数 \(+1\)。查询 \(x\) 的排名。
- 查询数据结构中排名为 \(x\) 的数。
- 求 \(x\) 的前驱(前驱定义为小于 \(x\),且最大的数)。
- 求 \(x\) 的后继(后继定义为大于 \(x\),且最小的数)。
代码略,刚好为上面的 \(6\) 个操作。
五、应用
5.1 文本编辑器和排名分裂
因为 FHQ_Treap 可以便捷地进行分裂与合并,所以能应用于文本编辑器,注意这里的分裂是“排名分裂”。
例2. P4008 [NOI2003] 文本编辑器
文本编辑器:由一段文本和该文本中的一个光标组成的,支持如下操作的数据结构。如果这段文本为空,我们就说这个文本编辑器是空的。
| 操作名称 | 输入文件中的格式 | 功能 |
|---|---|---|
| \(Move(k)\) | Move k | 将光标移动到第 \(k\) 个字符之后,如果 \(k=0\),将光标移到文本开头 |
| \(Insert(n,s)\) | Insert n s | 在光标处插入长度为 \(n\) 的字符串 \(s\),光标位置不变 \(n\geq1\) |
| \(Delete(n)\) | Delete n | 删除光标后的 \(n\) 个字符,光标位置不变,$n \geq$1 |
| \(Get(n)\) | Get n | 输出光标后的 \(n\) 个字符,光标位置不变,\(n \geq 1\) |
| \(Prev()\) | Prev | 光标前移一个字符 |
| \(Next()\) | Next | 光标后移一个字符 |
你的任务是:
-
建立一个空的文本编辑器。
-
从输入文件中读入一些操作并执行。
-
对所有执行过的
GET操作,将指定的内容写入输出文件。
与前面代码差不多,这里就只贴出主要部分:
void print(int u)
{
if(!u) return;
print(t[u].ls);
printf("%c",t[u].val);
print(t[u].rs);
}
int main()
{
srand(time(NULL));
scanf("%d",&n);
while(n--)
{
scanf("%s",opt);
if(opt[0]=='M') scanf("%d",&pos);
if(opt[0]=='I')
{
scanf("%d",&len);
split(root,pos,L,R);
for(int i=1;i<=len;i++)
{
char ch=getchar();
while(ch<32||ch>126) ch=getchar();
L=merge(L,newNode(ch));
}
root=merge(L,R);
}
if(opt[0]=='D')
{
scanf("%d",&len);
split(root,pos+len,L,R);
split(L,pos,L,p);
root=merge(L,R);
}
if(opt[0]=='G')
{
scanf("%d",&len);
split(root,pos+len,L,R);
split(L,pos,L,p);
print(p);
printf("\n");
root=merge(merge(L,p),R);
}
if(opt[0]=='P') --pos;
if(opt[0]=='N') ++pos;
}
return 0;
}
5.2 区间翻转
像线段树那样打上懒标记 Lazy-Tag 表示翻转即可,注意翻转不会破坏优先级 pri,操作类似于线段树的 push_down()。
例3. P3391 【模板】文艺平衡树
给定一个有序序列,翻转 \(m\) 个区间 \([l_i,r_i]\),求最终序列状态。
如原序列为 \(\{5 \ 4 \ 3 \ 2 \ 1 \}\),翻转区间为 \([2,4]\),那么反转后结果为 \(\{5\ 2 \ 3 \ 4 \ 1 \}\)。
注意,在这里的分裂操作为「排名分裂」,其余代码与标准的 FHQ_Treap 相同。
这里贴出重要部分:
void push_down(int u)//下传 Lazy 标记
{
if(!t[u].tag) return;
swap(t[u].ls,t[u].rs);//翻转 u 的左右部分,翻转不会破坏优先级 pri
t[t[u].ls].tag^=1;
t[t[u].rs].tag^=1;
t[u].tag=0;//与线段树类似
}
void split(int u,int x,int &L,int &R)
{
if(!u)
{
L=R=0;
return;
}
push_down(u);//处理 Lazy 标记
if(t[t[u].ls].siz+1<=x)
{
L=u;
split(t[u].rs,x-t[t[u].ls].siz-1,t[u].rs,R);
}
else
{
R=u;
split(t[u].ls,x,L,t[u].ls);
}
push_up(u);
}
int merge(int L,int R)
{
if(!L||!R) return L+R;
if(t[L].pri>t[R].pri)
{
push_down(L);//处理 Lazy 标记
t[L].rs=merge(t[L].rs,R);
push_up(L);
return L;
}
else
{
push_down(R);
t[R].ls=merge(L,t[R].ls);
push_up(R);
return R;
}
}
void inorder(int u)//中序遍历,打印结果
{
if(!u) return;
push_down(u);
inorder(t[u].ls);
printf("%d ",t[u].val);
inorder(t[u].rs);
}
5.3 可持久化平衡树
因为 FHQ_Treap 树的基本操作是分裂与合并,这两个操作对树的形态改变很小,所以符合可持久化的要求。在下面的 例4 中,由于每个合并操作前都需要分裂,所以合并不用再重复记录,实际情况要看相对应的题目。
例4. P5055 【模板】可持久化文艺平衡树
您需要写一种数据结构,来维护一个序列,其中需要提供以下操作(对于各个以往的历史版本):
- 在第 \(p\) 个数后插入数 \(x\)。
- 删除第 \(p\) 个数。
- 翻转区间 \([l,r]\)。
- 查询 \([l,r]\) 中所有数的和。
和原本平衡树不同的一点是,每一次的任何操作都是基于某一个历史版本,同时生成一个新的版本(操作 4 即保持原版本无变化),新版本即编号为此次操作的序号。
本题强制在线。
分裂是从一个从根到叶子的递归过程,每次递归返回 \(L\) 和 \(R\) 两棵树。若 \(L\) 和 \(R\) 有变化,则需要复制它们。注意只复制 \(L\) 和 \(R\) 的根即可,不需要复制整棵树,细节详见下面代码。
注意,FHQ_Treap 树的分裂可能导致较大的变化,所以需要很大的空间,需要依据题目给的时空限制去开空间。
这里给出完整代码:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+5;
int n,rt[N],L,R,p,cnt;
ll lastans;
struct FHQ_Treap
{
int ls,rs,val,pri,siz,tag;
ll sum;
}t[N<<7];
int newNode(int x)
{
cnt++;
t[cnt].ls=t[cnt].rs=0;
t[cnt].val=x;
t[cnt].pri=rand();
t[cnt].siz=1;
t[cnt].tag=0;
t[cnt].sum=x;
return cnt;
}
int clone(int u)//复制树 u,不需要复制整棵树,只复制根就行
{
int ret=newNode(0);
t[ret]=t[u];
return ret;
}
void update(int u)
{
t[u].siz=t[t[u].ls].siz+t[t[u].rs].siz+1;
t[u].sum=t[t[u].ls].sum+t[t[u].rs].sum+t[u].val;
}
void push_down(int u)
{
if(!t[u].tag) return;
if(t[u].ls) t[u].ls=clone(t[u].ls);
if(t[u].rs) t[u].rs=clone(t[u].rs);
swap(t[u].ls,t[u].rs);
t[t[u].ls].tag^=1;
t[t[u].rs].tag^=1;
t[u].tag=0;
}
void split(int u,int x,int &L,int &R)//排名分裂
{
if(!u)
{
L=R=0;
return;
}
push_down(u);
if(t[t[u].ls].siz+1<=x)//第 x 个数在 u 的右子树上
{
L=clone(u);//这个时间点的 L 是这个时间点 u 的副本
split(t[L].rs,x-t[t[u].ls].siz-1,t[L].rs,R);
update(L);
}
else
{
R=clone(u);//这个时间点的 R 是这个时间点 u 的副本
split(t[R].ls,x,L,t[R].ls);
update(R);
}
}
int merge(int L,int R)
{
if(!L||!R) return L+R;
push_down(L);
push_down(R);
if(t[L].pri>t[R].pri)
{
t[L].rs=merge(t[L].rs,R);
update(L);
return L;
}
else
{
t[R].ls=merge(L,t[R].ls);
update(R);
return R;
}
}
int main()
{
srand(time(0));
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int v,opt;
ll x,y;
scanf("%d%d",&v,&opt);
if(opt==1)//在第 x 个数后插入 y
{
scanf("%lld%lld",&x,&y);
x^=lastans;
y^=lastans;
split(rt[v],x,L,p);
rt[i]=merge(merge(L,newNode(y)),p);//记录在新的时间点上
}
if(opt==2)//删除第 x 个数
{
scanf("%lld",&x);
x^=lastans;
split(rt[v],x,L,R);
split(L,x-1,L,p);
rt[i]=merge(L,R);//记录在新的时间点上
}
if(opt==3)//翻转区间 [x.y]
{
scanf("%lld%lld",&x,&y);
x^=lastans;
y^=lastans;
split(rt[v],y,L,R);
split(L,x-1,L,p);
t[p].tag^=1;
rt[i]=merge(merge(L,p),R);//记录在新的时间点上
}
if(opt==4)//查询区间和 [x,y]
{
scanf("%lld%lld",&x,&y);
x^=lastans;
y^=lastans;
split(rt[v],y,L,R);
split(L,x-1,L,p);//p 树是区间 [x,y]
lastans=t[p].sum;
printf("%lld\n",lastans);
rt[i]=merge(merge(L,p),R);//记录在新的时间点上
}
}
return 0;
}
例5. P3835 【模板】可持久化平衡树
您需要写一种数据结构(可参考题目标题),来维护一个可重整数集合,其中需要提供以下操作(对于各个以往的历史版本):
- 插入 \(x\)。
- 删除 \(x\)(若有多个相同的数,应只删除一个,如果没有请忽略该操作)。
- 查询 \(x\) 的排名(排名定义为比当前数小的数的个数 \(+1\))。
- 查询排名为 \(x\) 的数。
- 求 \(x\) 的前驱(前驱定义为小于 \(x\),且最大的数,如不存在输出 \(-2^{31}+1\))
- 求 \(x\) 的后继(后继定义为大于 \(x\),且最小的数,如不存在输出 \(2^{31}-1\))
和原本平衡树不同的一点是,每一次的任何操作都是基于某一个历史版本,同时生成一个新的版本。(操作3, 4, 5, 6即保持原版本无变化)
每个版本的编号即为操作的序号(版本0即为初始状态,空树)
请读者自行思考并完成 例5。
咕咕咕先写到这里了,后面看有什么其他应用以及习题有时间再回来补吧(逃。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号