手写高斯混合聚类算法
参考资料:《机器学习》
原理
n维样本的高斯分布为:
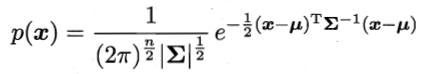
∑为协方差矩阵
由贝叶斯定理,样本Xj属于i类的后验概率为:
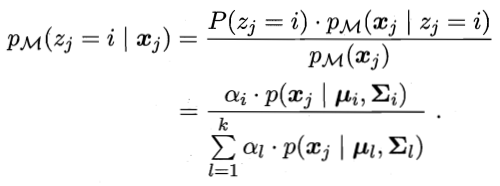
将上式简写为γji
则样本Xj分类公式为

给每一个分类一个系数,采用对数似然,得
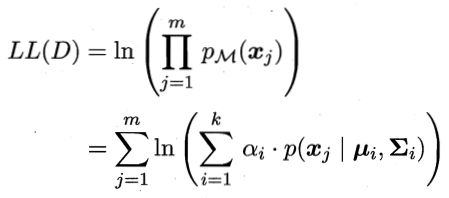
上式分别对∑,μ求导,令导数为0,得


系数求和为1,引入此约束,对数似然的拉格朗日形式为
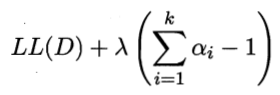
上式对系数α求导,令导数为0,得
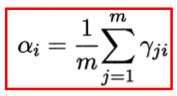
以上,红框部分即为参数更新公式,具体求导涉及标量对向量/矩阵的求导,一般采用微分法求解,请自行查阅求导规则。
算法流程为:

实现代码:
数据集
采用西瓜数据集4.0,如下
序号,密度,含糖量
1,0.697,0.460 2,0.774,0.376 3,0.634,0.264 4,0.608,0.318 5,0.556,0.215 6,0.403,0.237 7,0.481,0.149 8,0.437,0.211 9,0.666,0.091 10,0.243,0.267 11,0.245,0.057 12,0.343,0.099 13,0.639,0.161 14,0.657,0.198 15,0.360,0.370 16,0.593,0.042 17,0.719,0.103 18,0.359,0.188 19,0.339,0.241 20,0.282,0.257 21,0.748,0.232 22,0.714,0.346 23,0.483,0.312 24,0.478,0.437 25,0.525,0.369 26,0.751,0.489 27,0.532,0.472 28,0.473,0.376 29,0.725,0.445 30,0.446,0.459
代码
# 1 读取数据
file='xigua4.txt'
x=[]
with open(file) as f:
f.readline()
lines=f.read().split('\n')
for line in lines:
data=line.split(',')
x.append([float(data[-2]),float(data[-1])])
y=np.array(x)
# 2 算法部分
import numpy as np
import random
def probability(x,u,cov):
cov_inv=np.linalg.inv(cov)
cov_det=np.linalg.det(cov)
return np.exp(-1/2*((x-u).T.dot(cov_inv.dot(x-u))))/np.sqrt(cov_det)
def gauss_mixed_clustering(x,k=3,epochs=50,reload_params=None):
features_num=len(x[0])
r=np.empty(shape=(len(x),k))
# 初始化系数,均值向量和协方差矩阵
if reload_params!=None:
a,u,cov=reload_params
else:
a=np.random.uniform(size=k)
a/=np.sum(a)
u=np.array(random.sample(list(x),k))
cov=np.empty(shape=(k,features_num,features_num))
# 初始化为只有对角线不为0
for i in range(k):
for j in range(features_num):
cov[i][j]=[0]*j+[0.5]+[0]*(features_num-j-1)
step=0
while step<epochs:
# E步:计算r_ji
for j in range(len(x)):
for i in range(k):
r[j,i]=a[i]*probability(x[j],u[i],cov[i])
r[j]/=np.sum(r[j])
for i in range(k):
r_toal=np.sum(r[:,i])
u[i]=np.sum([x[j]*r[j,i] for j in range(len(x))],axis=0)/r_toal
cov[i]=np.sum([r[j,i]*((x[j]-u[i]).reshape((features_num,1)).dot((x[j]-u[i]).reshape((1,features_num)))) for j in range(len(x))],axis=0)/r_toal
a[i]=r_toal/len(x)
step+=1
C=[]
for i in range(k):
C.append([])
for j in range(len(x)):
c_j=np.argmax(r[j,:])
C[c_j].append(x[j])
return C,a,u,cov
验证
res,A,U,COV=gauss_mixed_clustering(y)
import matplotlib.pyplot as plt
%matplotlib inline
colors=['green','blue','red','black','yellow','orange']
for i in range(len(res)):
plt.scatter([d[0] for d in res[i]],[d[1] for d in res[i]],color=colors[i],label=str(i))
plt.scatter([d[0] for d in U],[d[1] for d in U],color=colors[-1],marker='^',label='center')
plt.xlabel('density')
plt.ylabel('suger')
plt.legend()
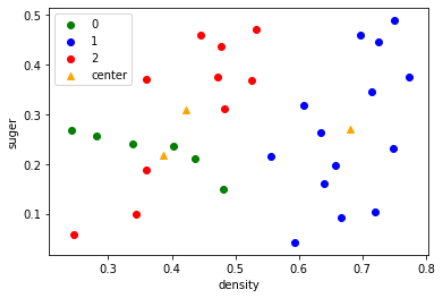
50轮后

# 100轮
res,A,U,COV=gauss_mixed_clustering(y,reload_params=[A,U,COV])
for i in range(len(res)):
plt.scatter([d[0] for d in res[i]],[d[1] for d in res[i]],color=colors[i],label=str(i))
plt.scatter([d[0] for d in U],[d[1] for d in U],color=colors[-1],marker='^',label='center')
plt.xlabel('density')
plt.ylabel('suger')
plt.legend()
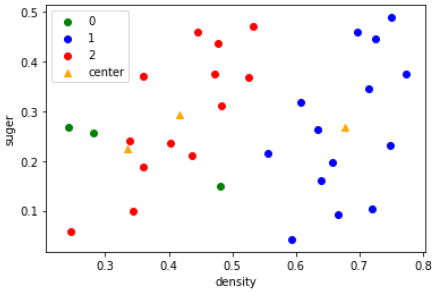
# 200轮后不再变化
res,A,U,COV=gauss_mixed_clustering(y,epochs=100,reload_params=[A,U,COV])
for i in range(len(res)):
plt.scatter([d[0] for d in res[i]],[d[1] for d in res[i]],color=colors[i],label=str(i))
plt.scatter([d[0] for d in U],[d[1] for d in U],color=colors[-1],marker='^',label='center')
plt.xlabel('density')
plt.ylabel('suger')
plt.legend()
总结
这个算法本身不复杂,可能涉及到矩阵求导的部分会麻烦一点。西瓜数据集太小了,收敛非常快。然后,这个算法同样对于初值敏感。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号